Streaming Sliced Optimal Transport

Sliced optimal transport (SOT) or sliced Wasserstein (SW) distance is widely recognized for its statistical and computational scalability. In this work, we further enhance the computational scalability by proposing the first method for computing SW from sample streams, called \emph{streaming sliced Wasserstein} (Stream-SW). To define Stream-SW, we first introduce the streaming computation of the one-dimensional Wasserstein distance. Since the one-dimensional Wasserstein (1DW) distance has a closed-form expression, given by the absolute difference between the quantile functions of the compared distributions, we leverage quantile approximation techniques for sample streams to define the streaming 1DW distance. By applying streaming 1DW to all projections, we obtain Stream-SW. The key advantage of Stream-SW is its low memory complexity while providing theoretical guarantees on the approximation error. We demonstrate that Stream-SW achieves a more accurate approximation of SW than random subsampling, with lower memory consumption, in comparing Gaussian distributions and mixtures of Gaussians from streaming samples. Additionally, we conduct experiments on point cloud classification, point cloud gradient flows, and streaming change point detection to further highlight the favorable performance of Stream-SW.

Model Tensor Planning

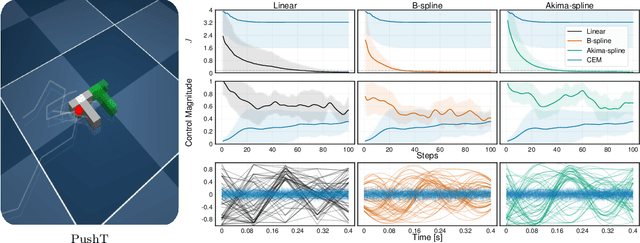
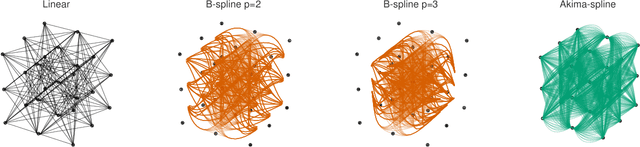
Sampling-based model predictive control (MPC) offers strong performance in nonlinear and contact-rich robotic tasks, yet often suffers from poor exploration due to locally greedy sampling schemes. We propose \emph{Model Tensor Planning} (MTP), a novel sampling-based MPC framework that introduces high-entropy control trajectory generation through structured tensor sampling. By sampling over randomized multipartite graphs and interpolating control trajectories with B-splines and Akima splines, MTP ensures smooth and globally diverse control candidates. We further propose a simple $\beta$-mixing strategy that blends local exploitative and global exploratory samples within the modified Cross-Entropy Method (CEM) update, balancing control refinement and exploration. Theoretically, we show that MTP achieves asymptotic path coverage and maximum entropy in the control trajectory space in the limit of infinite tensor depth and width. Our implementation is fully vectorized using JAX and compatible with MuJoCo XLA, supporting \emph{Just-in-time} (JIT) compilation and batched rollouts for real-time control with online domain randomization. Through experiments on various challenging robotic tasks, ranging from dexterous in-hand manipulation to humanoid locomotion, we demonstrate that MTP outperforms standard MPC and evolutionary strategy baselines in task success and control robustness. Design and sensitivity ablations confirm the effectiveness of MTP tensor sampling structure, spline interpolation choices, and mixing strategy. Altogether, MTP offers a scalable framework for robust exploration in model-based planning and control.

Improving Routing in Sparse Mixture of Experts with Graph of Tokens

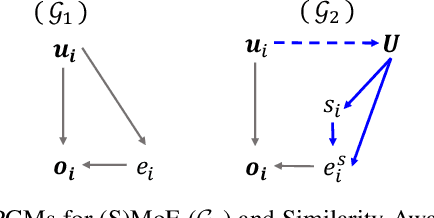
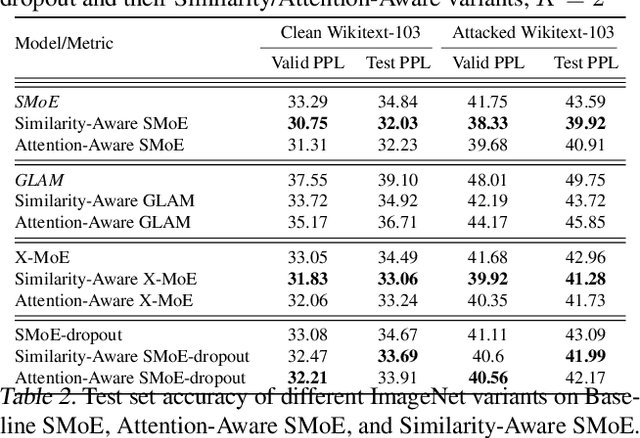
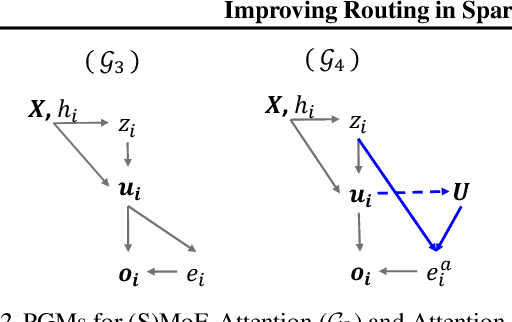
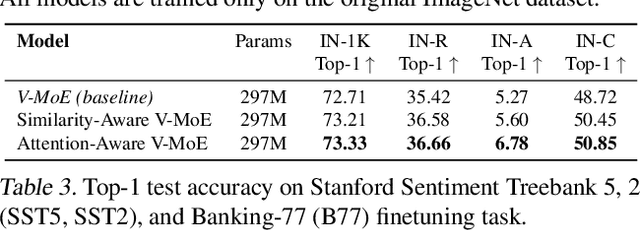
Sparse Mixture of Experts (SMoE) has emerged as a key to achieving unprecedented scalability in deep learning. By activating only a small subset of parameters per sample, SMoE achieves an exponential increase in parameter counts while maintaining a constant computational overhead. However, SMoE models are susceptible to routing fluctuations--changes in the routing of a given input to its target expert--at the late stage of model training, leading to model non-robustness. In this work, we unveil the limitation of SMoE through the perspective of the probabilistic graphical model (PGM). Through this PGM framework, we highlight the independence in the expert-selection of tokens, which exposes the model to routing fluctuation and non-robustness. Alleviating this independence, we propose the novel Similarity-Aware (S)MoE, which considers interactions between tokens during expert selection. We then derive a new PGM underlying an (S)MoE-Attention block, going beyond just a single (S)MoE layer. Leveraging the token similarities captured by the attention matrix, we propose the innovative Attention-Aware (S)MoE, which employs the attention matrix to guide the routing of tokens to appropriate experts in (S)MoE. We theoretically prove that Similarity/Attention-Aware routing help reduce the entropy of expert selection, resulting in more stable token routing mechanisms. We empirically validate our models on various tasks and domains, showing significant improvements in reducing routing fluctuations, enhancing accuracy, and increasing model robustness over the baseline MoE-Transformer with token routing via softmax gating.

Bayesian Density-Density Regression with Application to Cell-Cell Communications

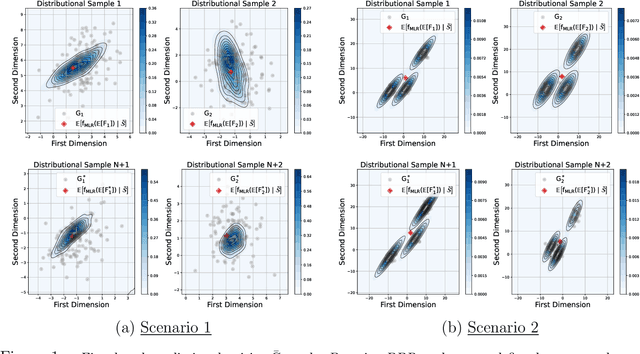
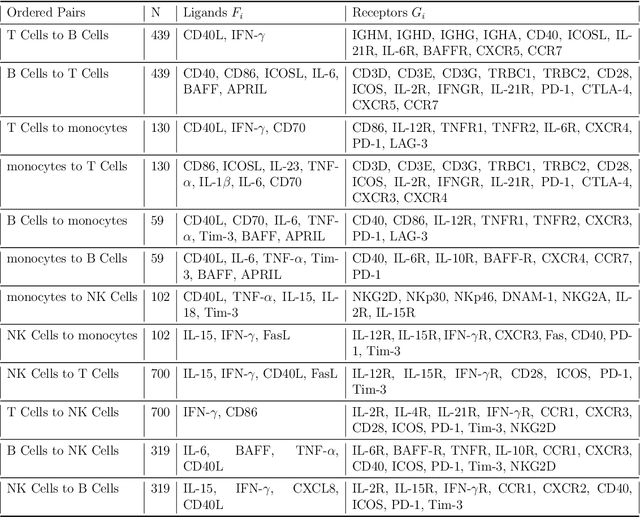
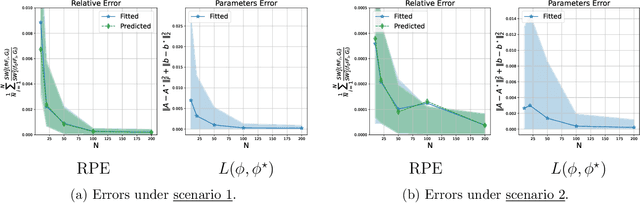
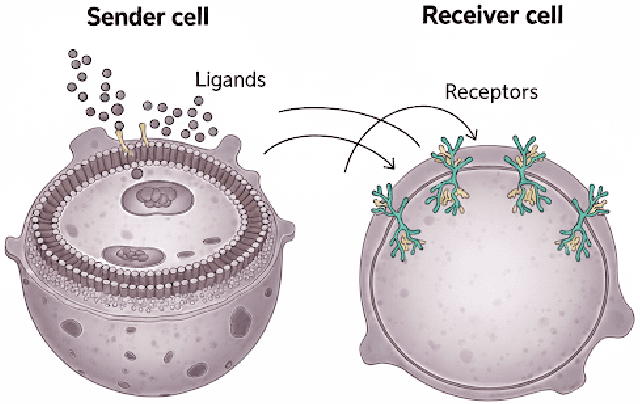
We introduce a scalable framework for regressing multivariate distributions onto multivariate distributions, motivated by the application of inferring cell-cell communication from population-scale single-cell data. The observed data consist of pairs of multivariate distributions for ligands from one cell type and corresponding receptors from another. For each ordered pair $e=(l,r)$ of cell types $(l \neq r)$ and each sample $i = 1, \ldots, n$, we observe a pair of distributions $(F_{ei}, G_{ei})$ of gene expressions for ligands and receptors of cell types $l$ and $r$, respectively. The aim is to set up a regression of receptor distributions $G_{ei}$ given ligand distributions $F_{ei}$. A key challenge is that these distributions reside in distinct spaces of differing dimensions. We formulate the regression of multivariate densities on multivariate densities using a generalized Bayes framework with the sliced Wasserstein distance between fitted and observed distributions. Finally, we use inference under such regressions to define a directed graph for cell-cell communications.

Unbiased Sliced Wasserstein Kernels for High-Quality Audio Captioning

Teacher-forcing training for audio captioning usually leads to exposure bias due to training and inference mismatch. Prior works propose the contrastive method to deal with caption degeneration. However, the contrastive method ignores the temporal information when measuring similarity across acoustic and linguistic modalities, leading to inferior performance. In this work, we develop the temporal-similarity score by introducing the unbiased sliced Wasserstein RBF (USW-RBF) kernel equipped with rotary positional embedding to account for temporal information across modalities. In contrast to the conventional sliced Wasserstein RBF kernel, we can form an unbiased estimation of USW-RBF kernel via Monte Carlo estimation. Therefore, it is well-suited to stochastic gradient optimization algorithms, and its approximation error decreases at a parametric rate of $\mathcal{O}(L^{-1/2})$ with $L$ Monte Carlo samples. Additionally, we introduce an audio captioning framework based on the unbiased sliced Wasserstein kernel, incorporating stochastic decoding methods to mitigate caption degeneration during the generation process. We conduct extensive quantitative and qualitative experiments on two datasets, AudioCaps and Clotho, to illustrate the capability of generating high-quality audio captions. Experimental results show that our framework is able to increase caption length, lexical diversity, and text-to-audio self-retrieval accuracy.

Lightspeed Geometric Dataset Distance via Sliced Optimal Transport

We introduce sliced optimal transport dataset distance (s-OTDD), a model-agnostic, embedding-agnostic approach for dataset comparison that requires no training, is robust to variations in the number of classes, and can handle disjoint label sets. The core innovation is Moment Transform Projection (MTP), which maps a label, represented as a distribution over features, to a real number. Using MTP, we derive a data point projection that transforms datasets into one-dimensional distributions. The s-OTDD is defined as the expected Wasserstein distance between the projected distributions, with respect to random projection parameters. Leveraging the closed form solution of one-dimensional optimal transport, s-OTDD achieves (near-)linear computational complexity in the number of data points and feature dimensions and is independent of the number of classes. With its geometrically meaningful projection, s-OTDD strongly correlates with the optimal transport dataset distance while being more efficient than existing dataset discrepancy measures. Moreover, it correlates well with the performance gap in transfer learning and classification accuracy in data augmentation.

Summarizing Bayesian Nonparametric Mixture Posterior -- Sliced Optimal Transport Metrics for Gaussian Mixtures

Existing methods to summarize posterior inference for mixture models focus on identifying a point estimate of the implied random partition for clustering, with density estimation as a secondary goal (Wade and Ghahramani, 2018; Dahl et al., 2022). We propose a novel approach for summarizing posterior inference in nonparametric Bayesian mixture models, prioritizing density estimation of the mixing measure (or mixture) as an inference target. One of the key features is the model-agnostic nature of the approach, which remains valid under arbitrarily complex dependence structures in the underlying sampling model. Using a decision-theoretic framework, our method identifies a point estimate by minimizing posterior expected loss. A loss function is defined as a discrepancy between mixing measures. Estimating the mixing measure implies inference on the mixture density and the random partition. Exploiting the discrete nature of the mixing measure, we use a version of sliced Wasserstein distance. We introduce two specific variants for Gaussian mixtures. The first, mixed sliced Wasserstein, applies generalized geodesic projections on the product of the Euclidean space and the manifold of symmetric positive definite matrices. The second, sliced mixture Wasserstein, leverages the linearity of Gaussian mixture measures for efficient projection.

Borrowing Strength in Distributionally Robust Optimization via Hierarchical Dirichlet Processes

This paper presents a novel optimization framework to address key challenges presented by modern machine learning applications: High dimensionality, distributional uncertainty, and data heterogeneity. Our approach unifies regularized estimation, distributionally robust optimization (DRO), and hierarchical Bayesian modeling in a single data-driven criterion. By employing a hierarchical Dirichlet process (HDP) prior, the method effectively handles multi-source data, achieving regularization, distributional robustness, and borrowing strength across diverse yet related data-generating processes. We demonstrate the method's advantages by establishing theoretical performance guarantees and tractable Monte Carlo approximations based on Dirichlet process (DP) theory. Numerical experiments validate the framework's efficacy in improving and stabilizing both prediction and parameter estimation accuracy, showcasing its potential for application in complex data environments.

Revisiting Deep Audio-Text Retrieval Through the Lens of Transportation

The Learning-to-match (LTM) framework proves to be an effective inverse optimal transport approach for learning the underlying ground metric between two sources of data, facilitating subsequent matching. However, the conventional LTM framework faces scalability challenges, necessitating the use of the entire dataset each time the parameters of the ground metric are updated. In adapting LTM to the deep learning context, we introduce the mini-batch Learning-to-match (m-LTM) framework for audio-text retrieval problems. This framework leverages mini-batch subsampling and Mahalanobis-enhanced family of ground metrics. Moreover, to cope with misaligned training data in practice, we propose a variant using partial optimal transport to mitigate the harm of misaligned data pairs in training data. We conduct extensive experiments on audio-text matching problems using three datasets: AudioCaps, Clotho, and ESC-50. Results demonstrate that our proposed method is capable of learning rich and expressive joint embedding space, which achieves SOTA performance. Beyond this, the proposed m-LTM framework is able to close the modality gap across audio and text embedding, which surpasses both triplet and contrastive loss in the zero-shot sound event detection task on the ESC-50 dataset. Notably, our strategy of employing partial optimal transport with m-LTM demonstrates greater noise tolerance than contrastive loss, especially under varying noise ratios in training data on the AudioCaps dataset. Our code is available at https://github.com/v-manhlt3/m-LTM-Audio-Text-Retrieval

Marginal Fairness Sliced Wasserstein Barycenter

The sliced Wasserstein barycenter (SWB) is a widely acknowledged method for efficiently generalizing the averaging operation within probability measure spaces. However, achieving marginal fairness SWB, ensuring approximately equal distances from the barycenter to marginals, remains unexplored. The uniform weighted SWB is not necessarily the optimal choice to obtain the desired marginal fairness barycenter due to the heterogeneous structure of marginals and the non-optimality of the optimization. As the first attempt to tackle the problem, we define the marginal fairness sliced Wasserstein barycenter (MFSWB) as a constrained SWB problem. Due to the computational disadvantages of the formal definition, we propose two hyperparameter-free and computationally tractable surrogate MFSWB problems that implicitly minimize the distances to marginals and encourage marginal fairness at the same time. To further improve the efficiency, we perform slicing distribution selection and obtain the third surrogate definition by introducing a new slicing distribution that focuses more on marginally unfair projecting directions. We discuss the relationship of the three proposed problems and their relationship to sliced multi-marginal Wasserstein distance. Finally, we conduct experiments on finding 3D point-clouds averaging, color harmonization, and training of sliced Wasserstein autoencoder with class-fairness representation to show the favorable performance of the proposed surrogate MFSWB problems.