Bayesian Density-Density Regression with Application to Cell-Cell Communications

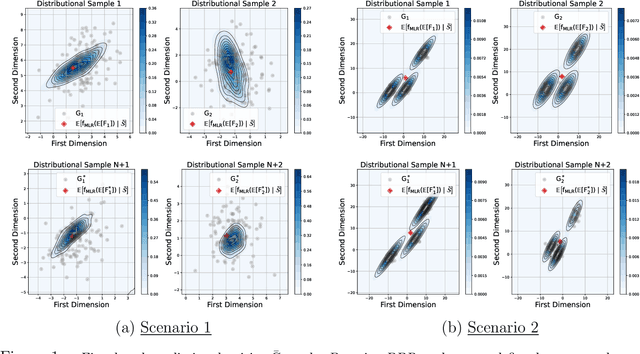
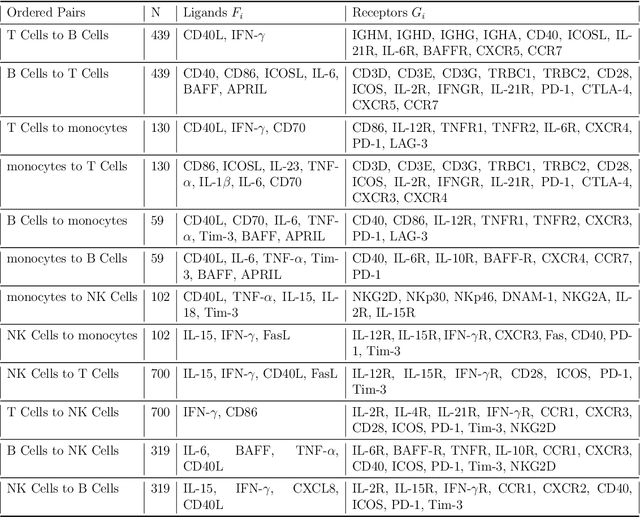
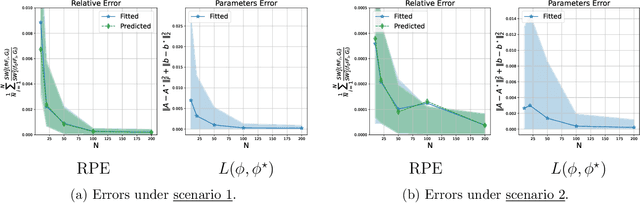
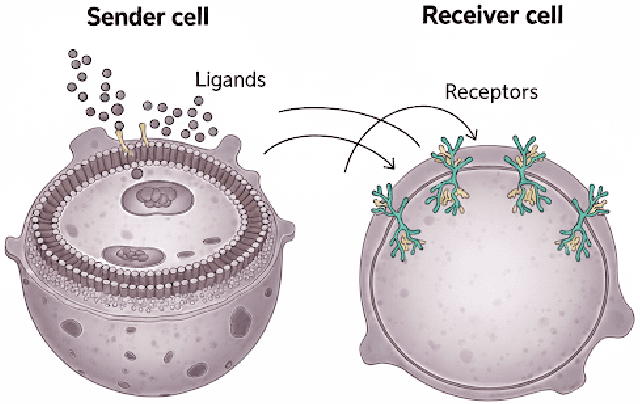
We introduce a scalable framework for regressing multivariate distributions onto multivariate distributions, motivated by the application of inferring cell-cell communication from population-scale single-cell data. The observed data consist of pairs of multivariate distributions for ligands from one cell type and corresponding receptors from another. For each ordered pair $e=(l,r)$ of cell types $(l \neq r)$ and each sample $i = 1, \ldots, n$, we observe a pair of distributions $(F_{ei}, G_{ei})$ of gene expressions for ligands and receptors of cell types $l$ and $r$, respectively. The aim is to set up a regression of receptor distributions $G_{ei}$ given ligand distributions $F_{ei}$. A key challenge is that these distributions reside in distinct spaces of differing dimensions. We formulate the regression of multivariate densities on multivariate densities using a generalized Bayes framework with the sliced Wasserstein distance between fitted and observed distributions. Finally, we use inference under such regressions to define a directed graph for cell-cell communications.