Distance-Based Tree-Sliced Wasserstein Distance

To overcome computational challenges of Optimal Transport (OT), several variants of Sliced Wasserstein (SW) has been developed in the literature. These approaches exploit the closed-form expression of the univariate OT by projecting measures onto (one-dimensional) lines. However, projecting measures onto low-dimensional spaces can lead to a loss of topological information. Tree-Sliced Wasserstein distance on Systems of Lines (TSW-SL) has emerged as a promising alternative that replaces these lines with a more advanced structure called tree systems. The tree structures enhance the ability to capture topological information of the metric while preserving computational efficiency. However, at the core of TSW-SL, the splitting maps, which serve as the mechanism for pushing forward measures onto tree systems, focus solely on the position of the measure supports while disregarding the projecting domains. Moreover, the specific splitting map used in TSW-SL leads to a metric that is not invariant under Euclidean transformations, a typically expected property for OT on Euclidean space. In this work, we propose a novel class of splitting maps that generalizes the existing one studied in TSW-SL enabling the use of all positional information from input measures, resulting in a novel Distance-based Tree-Sliced Wasserstein (Db-TSW) distance. In addition, we introduce a simple tree sampling process better suited for Db-TSW, leading to an efficient GPU-friendly implementation for tree systems, similar to the original SW. We also provide a comprehensive theoretical analysis of proposed class of splitting maps to verify the injectivity of the corresponding Radon Transform, and demonstrate that Db-TSW is an Euclidean invariant metric. We empirically show that Db-TSW significantly improves accuracy compared to recent SW variants while maintaining low computational cost via a wide range of experiments.

Spherical Tree-Sliced Wasserstein Distance

Sliced Optimal Transport (OT) simplifies the OT problem in high-dimensional spaces by projecting supports of input measures onto one-dimensional lines and then exploiting the closed-form expression of the univariate OT to reduce the computational burden of OT. Recently, the Tree-Sliced method has been introduced to replace these lines with more intricate structures, known as tree systems. This approach enhances the ability to capture topological information of integration domains in Sliced OT while maintaining low computational cost. Inspired by this approach, in this paper, we present an adaptation of tree systems on OT problems for measures supported on a sphere. As a counterpart to the Radon transform variant on tree systems, we propose a novel spherical Radon transform with a new integration domain called spherical trees. By leveraging this transform and exploiting the spherical tree structures, we derive closed-form expressions for OT problems on the sphere. Consequently, we obtain an efficient metric for measures on the sphere, named Spherical Tree-Sliced Wasserstein (STSW) distance. We provide an extensive theoretical analysis to demonstrate the topology of spherical trees and the well-definedness and injectivity of our Radon transform variant, which leads to an orthogonally invariant distance between spherical measures. Finally, we conduct a wide range of numerical experiments, including gradient flows and self-supervised learning, to assess the performance of our proposed metric, comparing it to recent benchmarks.

Tree-Sliced Wasserstein Distance on a System of Lines

Sliced Wasserstein (SW) distance in Optimal Transport (OT) is widely used in various applications thanks to its statistical effectiveness and computational efficiency. On the other hand, Tree Wassenstein (TW) and Tree-sliced Wassenstein (TSW) are instances of OT for probability measures where its ground cost is a tree metric. TSW also has a low computational complexity, i.e. linear to the number of edges in the tree. Especially, TSW is identical to SW when the tree is a chain. While SW is prone to loss of topological information of input measures due to relying on one-dimensional projection, TSW is more flexible and has a higher degree of freedom by choosing a tree rather than a line to alleviate the curse of dimensionality in SW. However, for practical applications, popular tree metric sampling methods are heavily built upon given supports, which limits their capacity to adapt to new supports. In this paper, we propose the Tree-Sliced Wasserstein distance on a System of Lines (TSW-SL), which brings a connection between SW and TSW. Compared to SW and TSW, our TSW-SL benefits from the higher degree of freedom of TSW while being suitable to dynamic settings as SW. In TSW-SL, we use a variant of the Radon Transform to project measures onto a system of lines, resulting in measures on a space with a tree metric, then leverage TW to efficiently compute distances between them. We empirically verify the advantages of TSW-SL over the traditional SW by conducting a variety of experiments on gradient flows, image style transfer, and generative models.

Mixture of Experts Meets Prompt-Based Continual Learning

Exploiting the power of pre-trained models, prompt-based approaches stand out compared to other continual learning solutions in effectively preventing catastrophic forgetting, even with very few learnable parameters and without the need for a memory buffer. While existing prompt-based continual learning methods excel in leveraging prompts for state-of-the-art performance, they often lack a theoretical explanation for the effectiveness of prompting. This paper conducts a theoretical analysis to unravel how prompts bestow such advantages in continual learning, thus offering a new perspective on prompt design. We first show that the attention block of pre-trained models like Vision Transformers inherently encodes a special mixture of experts architecture, characterized by linear experts and quadratic gating score functions. This realization drives us to provide a novel view on prefix tuning, reframing it as the addition of new task-specific experts, thereby inspiring the design of a novel gating mechanism termed Non-linear Residual Gates (NoRGa). Through the incorporation of non-linear activation and residual connection, NoRGa enhances continual learning performance while preserving parameter efficiency. The effectiveness of NoRGa is substantiated both theoretically and empirically across diverse benchmarks and pretraining paradigms.

Statistical Advantages of Perturbing Cosine Router in Sparse Mixture of Experts

The cosine router in sparse Mixture of Experts (MoE) has recently emerged as an attractive alternative to the conventional linear router. Indeed, the cosine router demonstrates favorable performance in image and language tasks and exhibits better ability to mitigate the representation collapse issue, which often leads to parameter redundancy and limited representation potentials. Despite its empirical success, a comprehensive analysis of the cosine router in sparse MoE has been lacking. Considering the least square estimation of the cosine routing sparse MoE, we demonstrate that due to the intrinsic interaction of the model parameters in the cosine router via some partial differential equations, regardless of the structures of the experts, the estimation rates of experts and model parameters can be as slow as $\mathcal{O}(1/\log^{\tau}(n))$ where $\tau > 0$ is some constant and $n$ is the sample size. Surprisingly, these pessimistic non-polynomial convergence rates can be circumvented by the widely used technique in practice to stabilize the cosine router -- simply adding noises to the $\mathbb{L}_{2}$ norms in the cosine router, which we refer to as \textit{perturbed cosine router}. Under the strongly identifiable settings of the expert functions, we prove that the estimation rates for both the experts and model parameters under the perturbed cosine routing sparse MoE are significantly improved to polynomial rates. Finally, we conduct extensive simulation studies in both synthetic and real data settings to empirically validate our theoretical results.

Relational dynamic memory networks

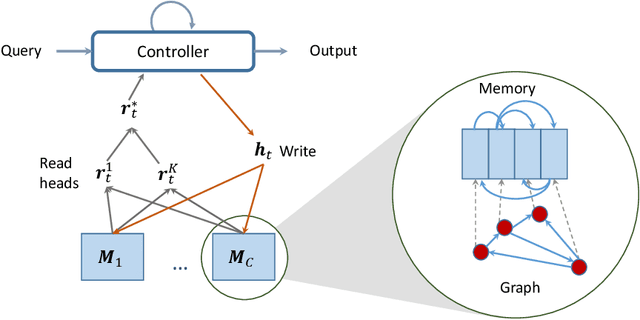
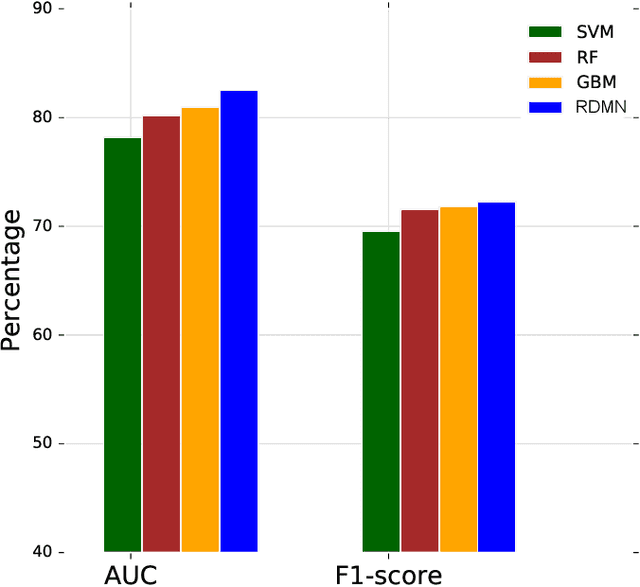
Neural networks excel in detecting regular patterns but are less successful in representing and manipulating complex data structures, possibly due to the lack of an external memory. This has led to the recent development of a new line of architectures known as Memory-Augmented Neural Networks (MANNs), each of which consists of a neural network that interacts with an external memory matrix. However, this RAM-like memory matrix is unstructured and thus does not naturally encode structured objects. Here we design a new MANN dubbed Relational Dynamic Memory Network (RMDN) to bridge the gap. Like existing MANNs, RMDN has a neural controller but its memory is structured as multi-relational graphs. RMDN uses the memory to represent and manipulate graph-structured data in response to query; and as a neural network, RMDN is trainable from labeled data. Thus RMDN learns to answer queries about a set of graph-structured objects without explicit programming. We evaluate the capability of RMDN on several important prediction problems, including software vulnerability, molecular bioactivity and chemical-chemical interaction. Results demonstrate the efficacy of the proposed model.

Graph Memory Networks for Molecular Activity Prediction

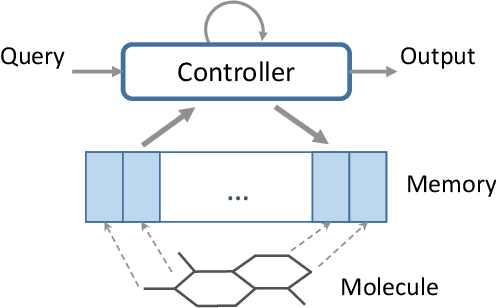
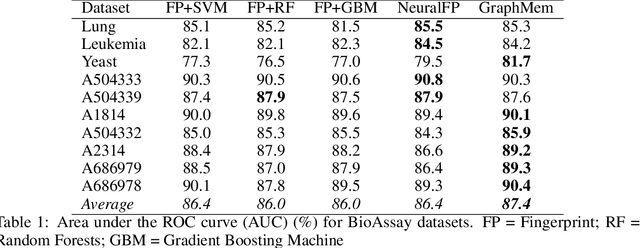
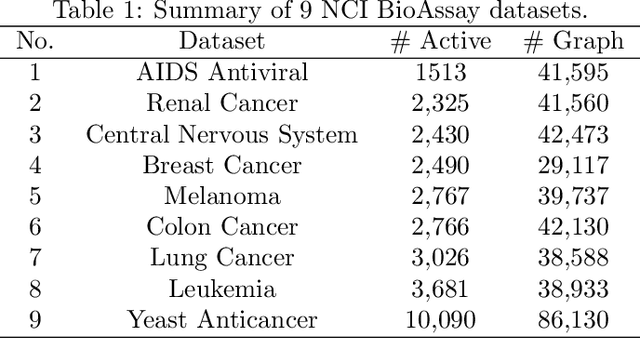
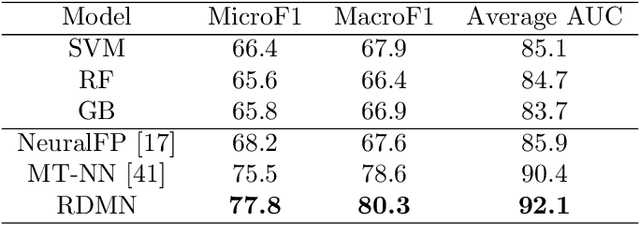
Molecular activity prediction is critical in drug design. Machine learning techniques such as kernel methods and random forests have been successful for this task. These models require fixed-size feature vectors as input while the molecules are variable in size and structure. As a result, fixed-size fingerprint representation is poor in handling substructures for large molecules. In addition, molecular activity tests, or a so-called BioAssays, are relatively small in the number of tested molecules due to its complexity. Here we approach the problem through deep neural networks as they are flexible in modeling structured data such as grids, sequences and graphs. We train multiple BioAssays using a multi-task learning framework, which combines information from multiple sources to improve the performance of prediction, especially on small datasets. We propose Graph Memory Network (GraphMem), a memory-augmented neural network to model the graph structure in molecules. GraphMem consists of a recurrent controller coupled with an external memory whose cells dynamically interact and change through a multi-hop reasoning process. Applied to the molecules, the dynamic interactions enable an iterative refinement of the representation of molecular graphs with multiple bond types. GraphMem is capable of jointly training on multiple datasets by using a specific-task query fed to the controller as an input. We demonstrate the effectiveness of the proposed model for separately and jointly training on more than 100K measurements, spanning across 9 BioAssay activity tests.

Graph Classification via Deep Learning with Virtual Nodes

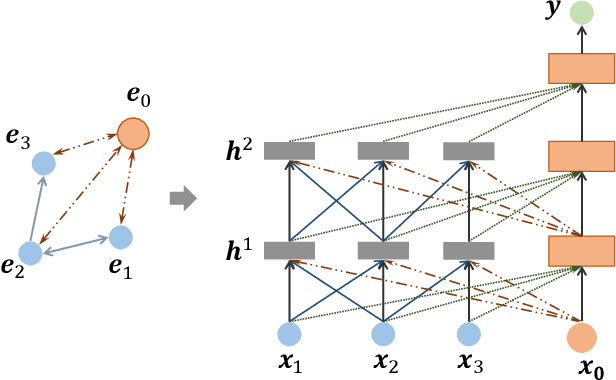
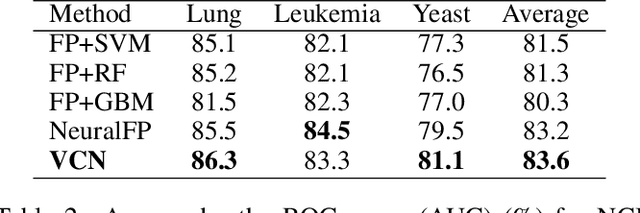
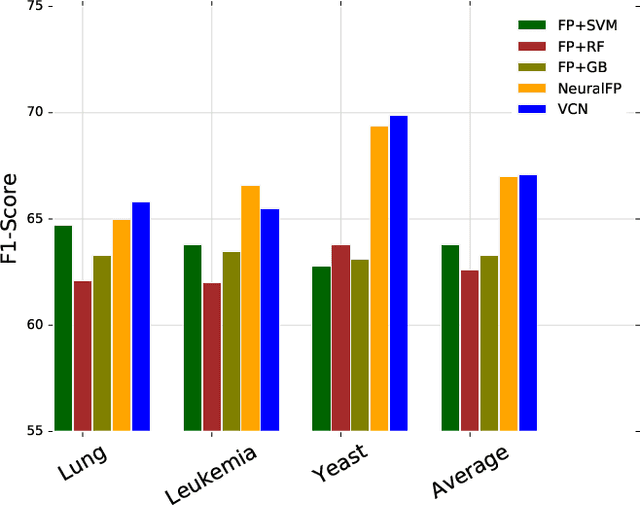
Learning representation for graph classification turns a variable-size graph into a fixed-size vector (or matrix). Such a representation works nicely with algebraic manipulations. Here we introduce a simple method to augment an attributed graph with a virtual node that is bidirectionally connected to all existing nodes. The virtual node represents the latent aspects of the graph, which are not immediately available from the attributes and local connectivity structures. The expanded graph is then put through any node representation method. The representation of the virtual node is then the representation of the entire graph. In this paper, we use the recently introduced Column Network for the expanded graph, resulting in a new end-to-end graph classification model dubbed Virtual Column Network (VCN). The model is validated on two tasks: (i) predicting bio-activity of chemical compounds, and (ii) finding software vulnerability from source code. Results demonstrate that VCN is competitive against well-established rivals.

DeepCare: A Deep Dynamic Memory Model for Predictive Medicine

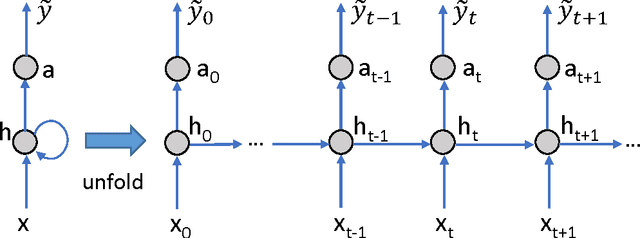
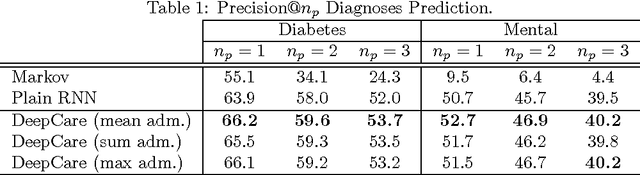
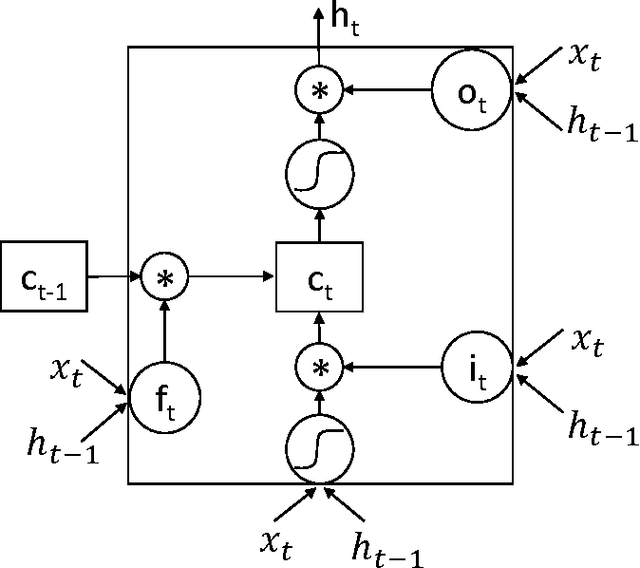
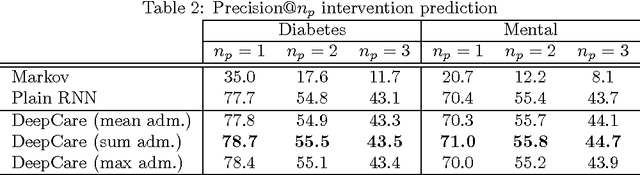
Personalized predictive medicine necessitates the modeling of patient illness and care processes, which inherently have long-term temporal dependencies. Healthcare observations, recorded in electronic medical records, are episodic and irregular in time. We introduce DeepCare, an end-to-end deep dynamic neural network that reads medical records, stores previous illness history, infers current illness states and predicts future medical outcomes. At the data level, DeepCare represents care episodes as vectors in space, models patient health state trajectories through explicit memory of historical records. Built on Long Short-Term Memory (LSTM), DeepCare introduces time parameterizations to handle irregular timed events by moderating the forgetting and consolidation of memory cells. DeepCare also incorporates medical interventions that change the course of illness and shape future medical risk. Moving up to the health state level, historical and present health states are then aggregated through multiscale temporal pooling, before passing through a neural network that estimates future outcomes. We demonstrate the efficacy of DeepCare for disease progression modeling, intervention recommendation, and future risk prediction. On two important cohorts with heavy social and economic burden -- diabetes and mental health -- the results show improved modeling and risk prediction accuracy.

One Size Fits Many: Column Bundle for Multi-X Learning

Much recent machine learning research has been directed towards leveraging shared statistics among labels, instances and data views, commonly referred to as multi-label, multi-instance and multi-view learning. The underlying premises are that there exist correlations among input parts and among output targets, and the predictive performance would increase when the correlations are incorporated. In this paper, we propose Column Bundle (CLB), a novel deep neural network for capturing the shared statistics in data. CLB is generic that the same architecture can be applied for various types of shared statistics by changing only input and output handling. CLB is capable of scaling to thousands of input parts and output labels by avoiding explicit modeling of pairwise relations. We evaluate CLB on different types of data: (a) multi-label, (b) multi-view, (c) multi-view/multi-label and (d) multi-instance. CLB demonstrates a comparable and competitive performance in all datasets against state-of-the-art methods designed specifically for each type.