Loss-based Bayesian Sequential Prediction of Value at Risk with a Long-Memory and Non-linear Realized Volatility Model

A long memory and non-linear realized volatility model class is proposed for direct Value at Risk (VaR) forecasting. This model, referred to as RNN-HAR, extends the heterogeneous autoregressive (HAR) model, a framework known for efficiently capturing long memory in realized measures, by integrating a Recurrent Neural Network (RNN) to handle non-linear dynamics. Loss-based generalized Bayesian inference with Sequential Monte Carlo is employed for model estimation and sequential prediction in RNN HAR. The empirical analysis is conducted using daily closing prices and realized measures from 2000 to 2022 across 31 market indices. The proposed models one step ahead VaR forecasting performance is compared against a basic HAR model and its extensions. The results demonstrate that the proposed RNN-HAR model consistently outperforms all other models considered in the study.

DeepVol: A Deep Transfer Learning Approach for Universal Asset Volatility Modeling

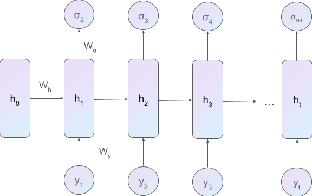
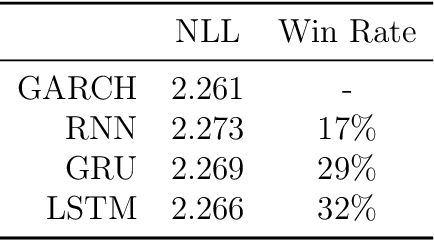
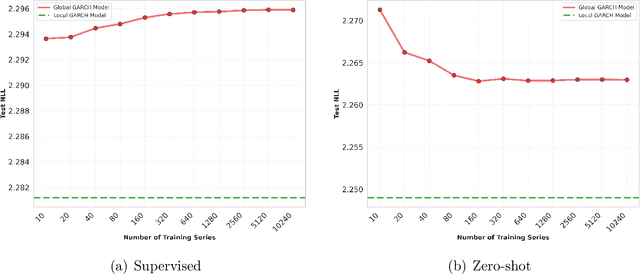
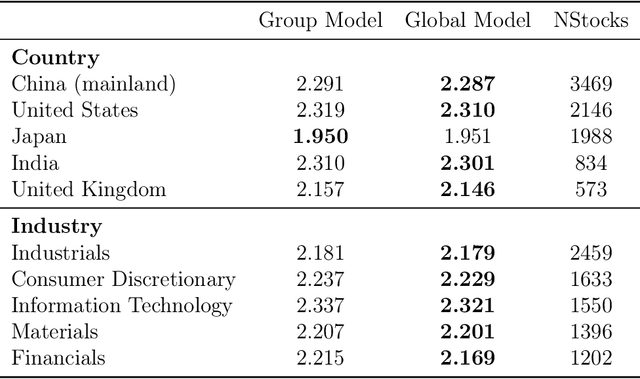
This paper introduces DeepVol, a promising new deep learning volatility model that outperforms traditional econometric models in terms of model generality. DeepVol leverages the power of transfer learning to effectively capture and model the volatility dynamics of all financial assets, including previously unseen ones, using a single universal model. This contrasts to the prevailing practice in econometrics literature, which necessitates training separate models for individual datasets. The introduction of DeepVol opens up new avenues for volatility modeling and forecasting in the finance industry, potentially transforming the way volatility is understood and predicted.

Wasserstein Gaussianization and Efficient Variational Bayes for Robust Bayesian Synthetic Likelihood

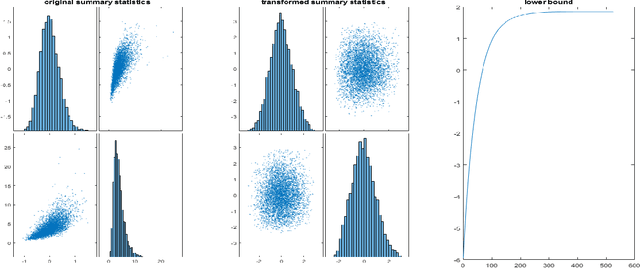
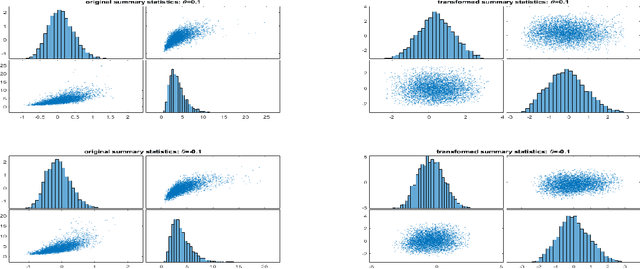
The Bayesian Synthetic Likelihood (BSL) method is a widely-used tool for likelihood-free Bayesian inference. This method assumes that some summary statistics are normally distributed, which can be incorrect in many applications. We propose a transformation, called the Wasserstein Gaussianization transformation, that uses a Wasserstein gradient flow to approximately transform the distribution of the summary statistics into a Gaussian distribution. BSL also implicitly requires compatibility between simulated summary statistics under the working model and the observed summary statistics. A robust BSL variant which achieves this has been developed in the recent literature. We combine the Wasserstein Gaussianization transformation with robust BSL, and an efficient Variational Bayes procedure for posterior approximation, to develop a highly efficient and reliable approximate Bayesian inference method for likelihood-free problems.

Particle Mean Field Variational Bayes

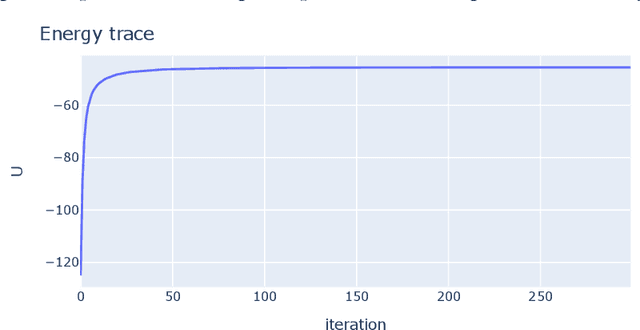
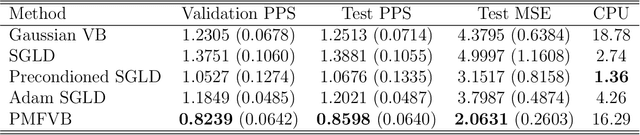
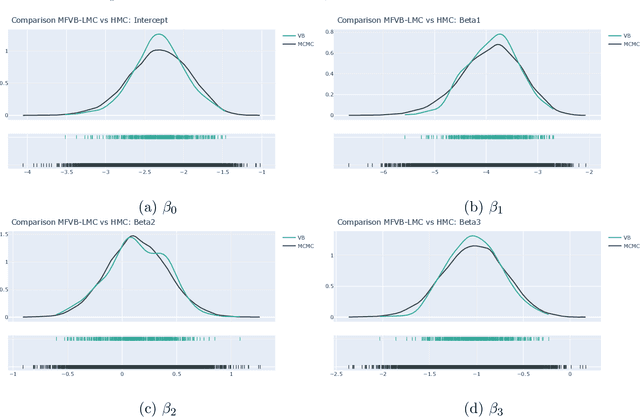
The Mean Field Variational Bayes (MFVB) method is one of the most computationally efficient techniques for Bayesian inference. However, its use has been restricted to models with conjugate priors or those that require analytical calculations. This paper proposes a novel particle-based MFVB approach that greatly expands the applicability of the MFVB method. We establish the theoretical basis of the new method by leveraging the connection between Wasserstein gradient flows and Langevin diffusion dynamics, and demonstrate the effectiveness of this approach using Bayesian logistic regression, stochastic volatility, and deep neural networks.

Realized recurrent conditional heteroskedasticity model for volatility modelling

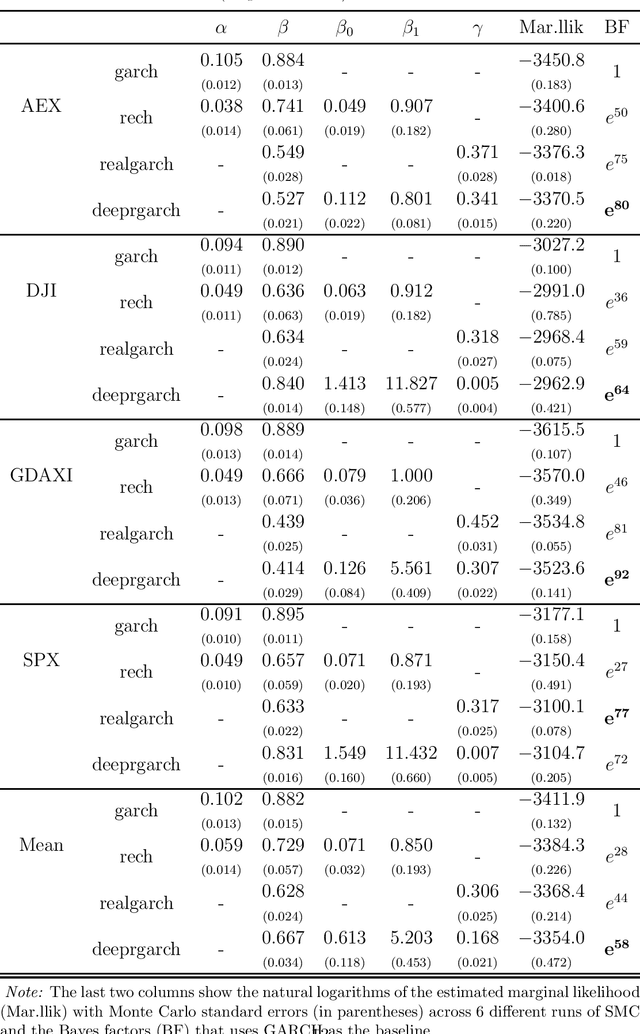
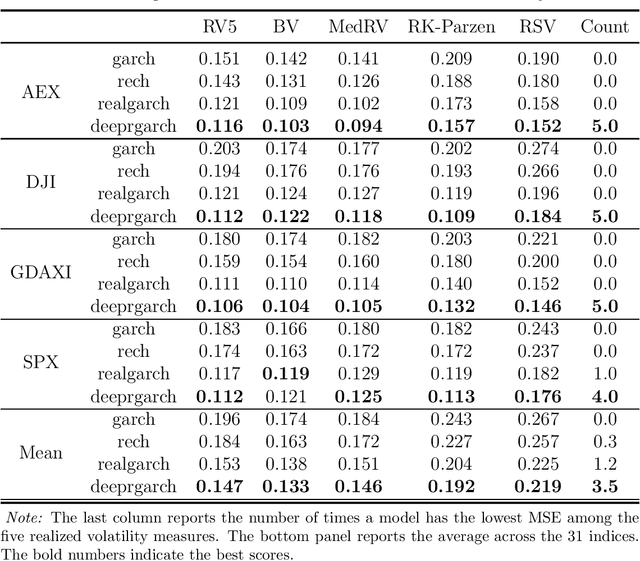
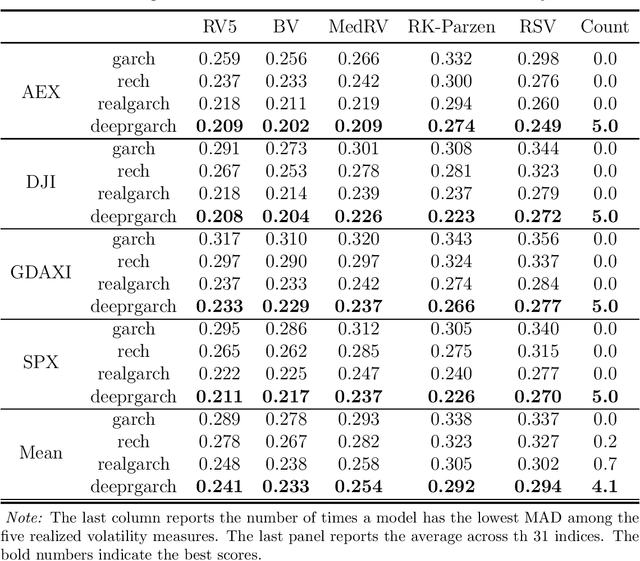
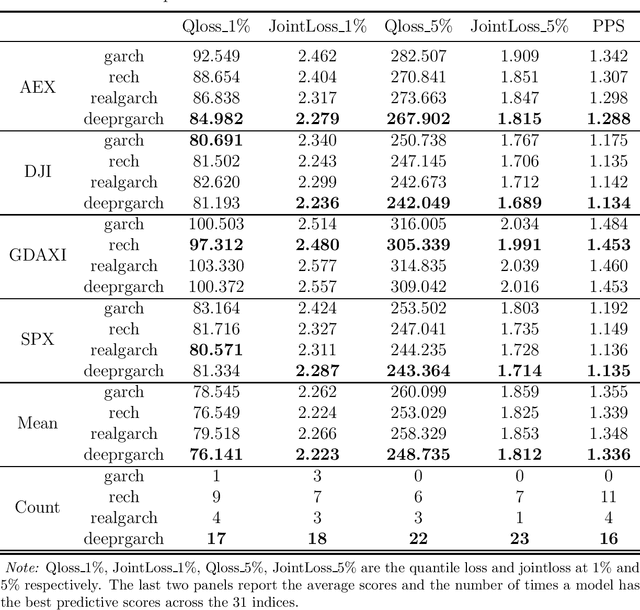
We propose a new approach to volatility modelling by combining deep learning (LSTM) and realized volatility measures. This LSTM-enhanced realized GARCH framework incorporates and distills modeling advances from financial econometrics, high frequency trading data and deep learning. Bayesian inference via the Sequential Monte Carlo method is employed for statistical inference and forecasting. The new framework can jointly model the returns and realized volatility measures, has an excellent in-sample fit and superior predictive performance compared to several benchmark models, while being able to adapt well to the stylized facts in volatility. The performance of the new framework is tested using a wide range of metrics, from marginal likelihood, volatility forecasting, to tail risk forecasting and option pricing. We report on a comprehensive empirical study using 31 widely traded stock indices over a time period that includes COVID-19 pandemic.

An Introduction to Quantum Computing for Statisticians

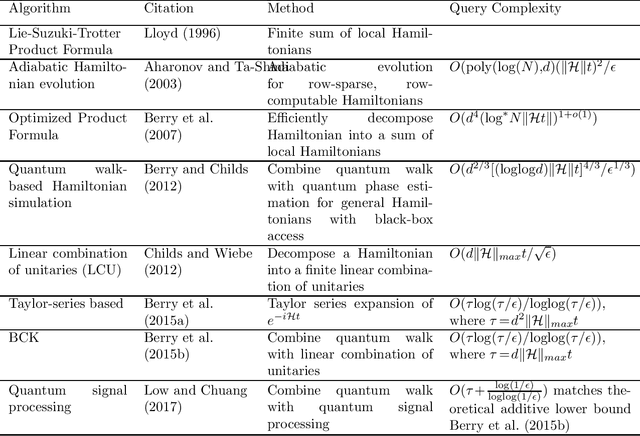
Quantum computing has the potential to revolutionise and change the way we live and understand the world. This review aims to provide an accessible introduction to quantum computing with a focus on applications in statistics and data analysis. We start with an introduction to the basic concepts necessary to understand quantum computing and the differences between quantum and classical computing. We describe the core quantum subroutines that serve as the building blocks of quantum algorithms. We then review a range of quantum algorithms expected to deliver a computational advantage in statistics and machine learning. We highlight the challenges and opportunities in applying quantum computing to problems in statistics and discuss potential future research directions.

Quantum Natural Gradient for Variational Bayes

Variational Bayes (VB) is a critical method in machine learning and statistics, underpinning the recent success of Bayesian deep learning. The natural gradient is an essential component of efficient VB estimation, but it is prohibitively computationally expensive in high dimensions. We propose a hybrid quantum-classical algorithm to improve the scaling properties of natural gradient computation and make VB a truly computationally efficient method for Bayesian inference in highdimensional settings. The algorithm leverages matrix inversion from the linear systems algorithm by Harrow, Hassidim, and Lloyd [Phys. Rev. Lett. 103, 15 (2009)] (HHL). We demonstrate that the matrix to be inverted is sparse and the classical-quantum-classical handoffs are sufficiently economical to preserve computational efficiency, making the problem of natural gradient for VB an ideal application of HHL. We prove that, under standard conditions, the VB algorithm with quantum natural gradient is guaranteed to converge. Our regression-based natural gradient formulation is also highly useful for classical VB.

A practical tutorial on Variational Bayes

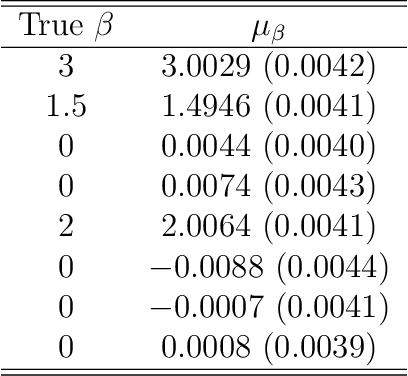
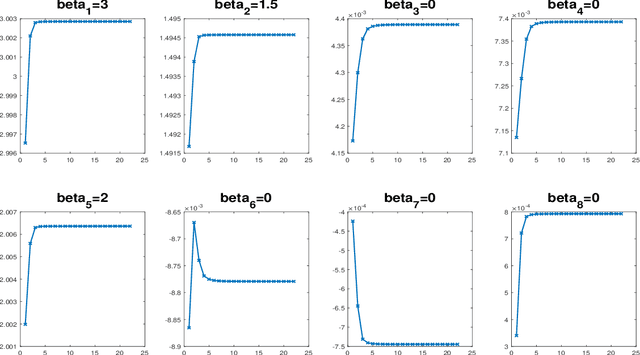
This tutorial gives a quick introduction to Variational Bayes (VB), also called Variational Inference or Variational Approximation, from a practical point of view. The paper covers a range of commonly used VB methods and an attempt is made to keep the materials accessible to the wide community of data analysis practitioners. The aim is that the reader can quickly derive and implement their first VB algorithm for Bayesian inference with their data analysis problem. An end-user software package in Matlab together with the documentation can be found at https://vbayeslab.github.io/VBLabDocs/

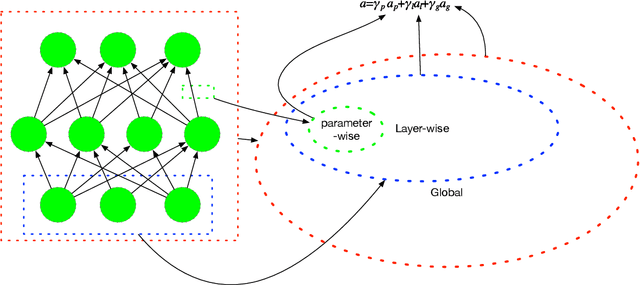
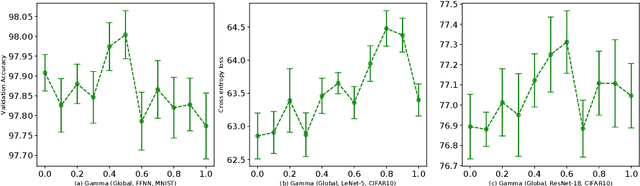
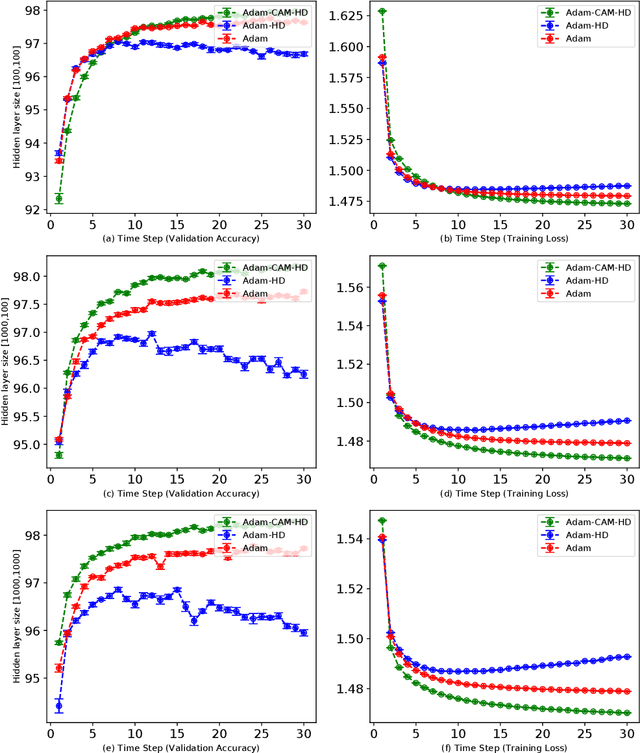
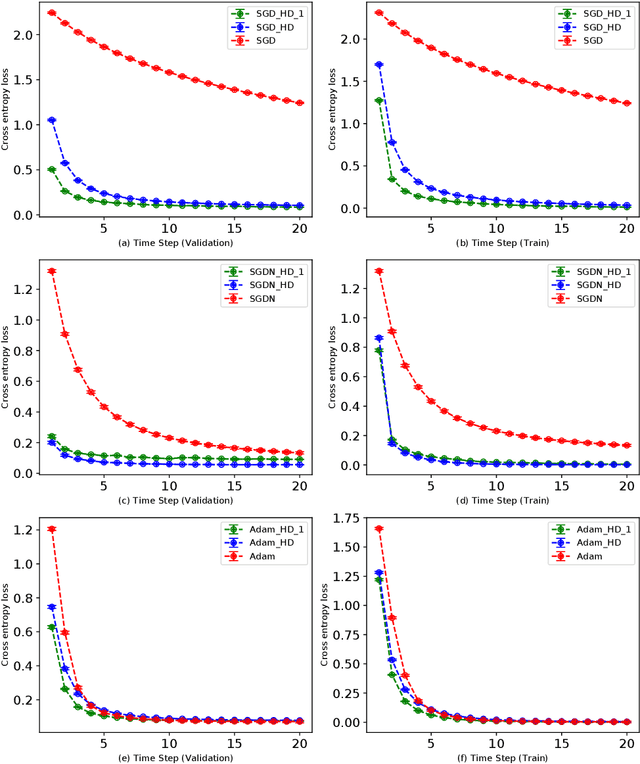
Adaptive Multi-level Hyper-gradient Descent

Adaptive learning rates can lead to faster convergence and better final performance for deep learning models. There are several widely known human-designed adaptive optimizers such as Adam and RMSProp, gradient based adaptive methods such as hyper-descent and L4, and meta learning approaches including learning to learn. However, the issue of balancing adaptiveness and over-parameterization is still a topic to be addressed. In this study, we investigate different levels of learning rate adaptation based on the framework of hyper-gradient descent, and further propose a method that adaptively learns the model parameters for combining different levels of adaptations. Meanwhile, we show the relationship between adding regularization on over-parameterized learning rates and building combinations of different levels of adaptive learning rates. The experiments on several network architectures including feed-forward networks, LeNet-5 and ResNet-34 show that the proposed multi-level adaptive approach can outperform baseline adaptive methods in a variety circumstances with statistical significance.

A Bayesian Long Short-Term Memory Model for Value at Risk and Expected Shortfall Joint Forecasting

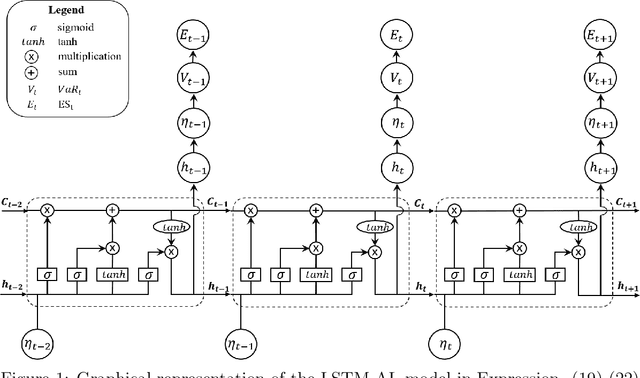
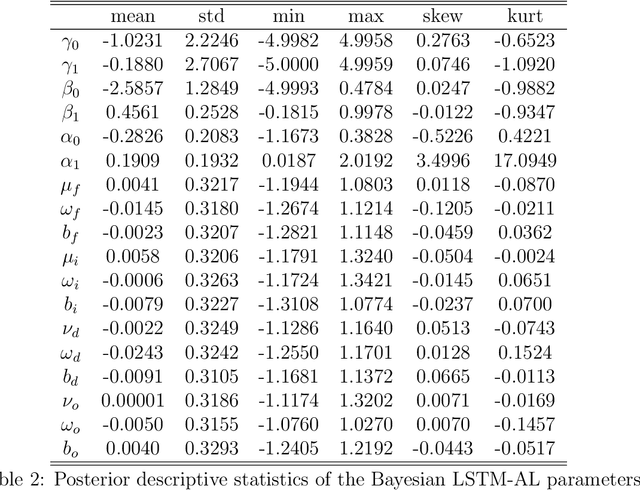
Value-at-Risk (VaR) and Expected Shortfall (ES) are widely used in the financial sector to measure the market risk and manage the extreme market movement. The recent link between the quantile score function and the Asymmetric Laplace density has led to a flexible likelihood-based framework for joint modelling of VaR and ES. It is of high interest in financial applications to be able to capture the underlying joint dynamics of these two quantities. We address this problem by developing a hybrid model that is based on the Asymmetric Laplace quasi-likelihood and employs the Long Short-Term Memory (LSTM) time series modelling technique from Machine Learning to capture efficiently the underlying dynamics of VaR and ES. We refer to this model as LSTM-AL. We adopt the adaptive Markov chain Monte Carlo (MCMC) algorithm for Bayesian inference in the LSTM-AL model. Empirical results show that the proposed LSTM-AL model can improve the VaR and ES forecasting accuracy over a range of well-established competing models.