An Introduction to Quantum Computing for Statisticians

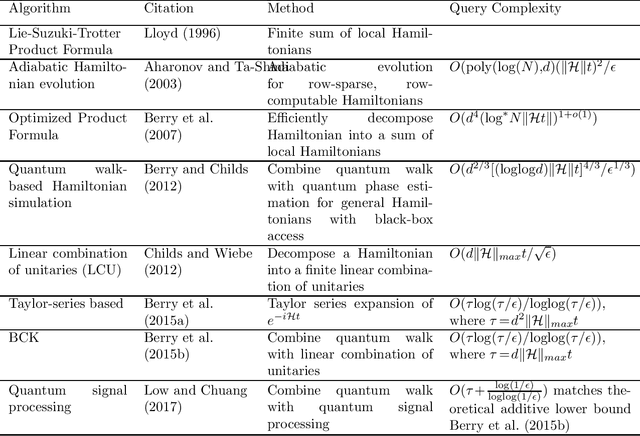
Quantum computing has the potential to revolutionise and change the way we live and understand the world. This review aims to provide an accessible introduction to quantum computing with a focus on applications in statistics and data analysis. We start with an introduction to the basic concepts necessary to understand quantum computing and the differences between quantum and classical computing. We describe the core quantum subroutines that serve as the building blocks of quantum algorithms. We then review a range of quantum algorithms expected to deliver a computational advantage in statistics and machine learning. We highlight the challenges and opportunities in applying quantum computing to problems in statistics and discuss potential future research directions.

Quantum Natural Gradient for Variational Bayes

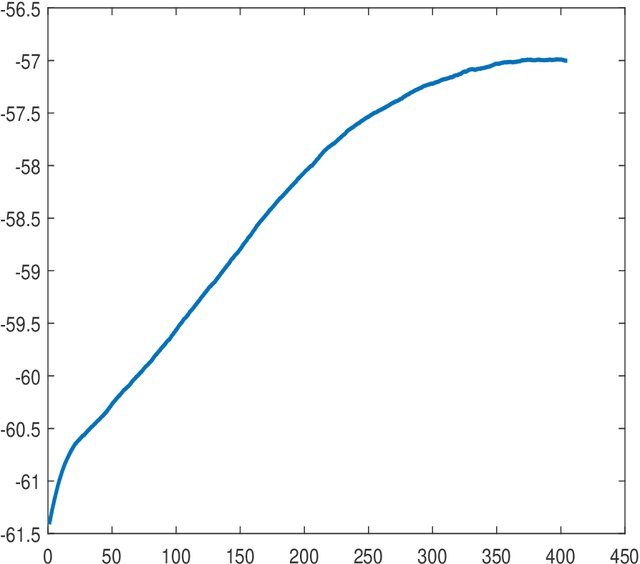
Variational Bayes (VB) is a critical method in machine learning and statistics, underpinning the recent success of Bayesian deep learning. The natural gradient is an essential component of efficient VB estimation, but it is prohibitively computationally expensive in high dimensions. We propose a hybrid quantum-classical algorithm to improve the scaling properties of natural gradient computation and make VB a truly computationally efficient method for Bayesian inference in highdimensional settings. The algorithm leverages matrix inversion from the linear systems algorithm by Harrow, Hassidim, and Lloyd [Phys. Rev. Lett. 103, 15 (2009)] (HHL). We demonstrate that the matrix to be inverted is sparse and the classical-quantum-classical handoffs are sufficiently economical to preserve computational efficiency, making the problem of natural gradient for VB an ideal application of HHL. We prove that, under standard conditions, the VB algorithm with quantum natural gradient is guaranteed to converge. Our regression-based natural gradient formulation is also highly useful for classical VB.