Generalized Laplacian Regularized Framelet GCNs

This paper introduces a novel Framelet Graph approach based on p-Laplacian GNN. The proposed two models, named p-Laplacian undecimated framelet graph convolution (pL-UFG) and generalized p-Laplacian undecimated framelet graph convolution (pL-fUFG) inherit the nature of p-Laplacian with the expressive power of multi-resolution decomposition of graph signals. The empirical study highlights the excellent performance of the pL-UFG and pL-fUFG in different graph learning tasks including node classification and signal denoising.

Regularized Flexible Activation Function Combinations for Deep Neural Networks

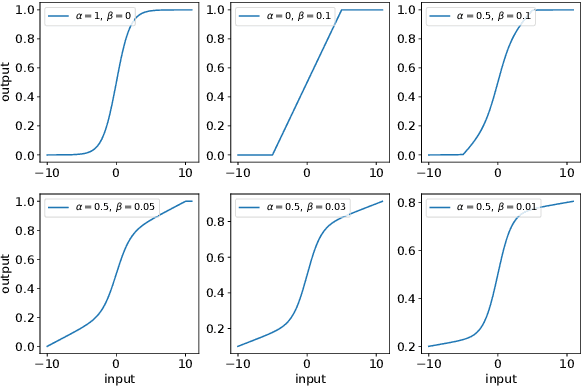
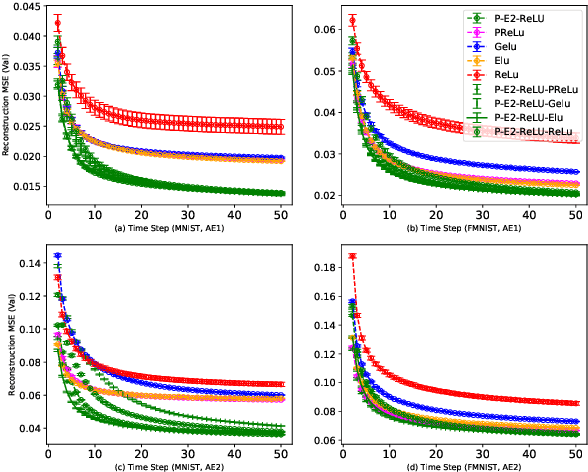
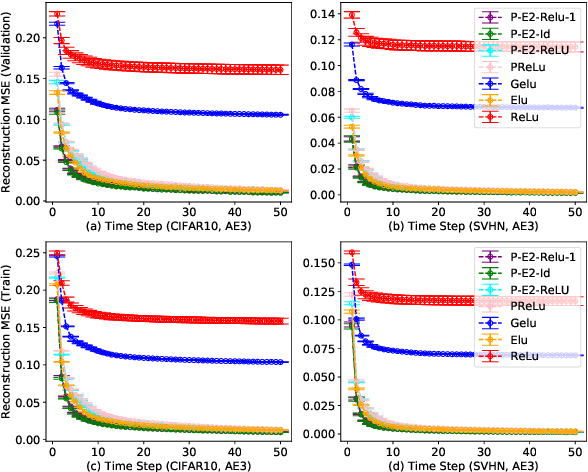
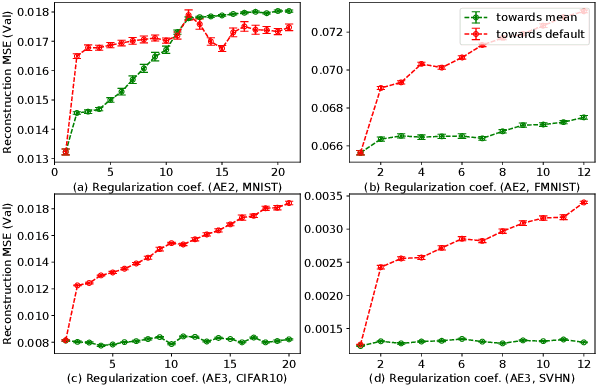
Activation in deep neural networks is fundamental to achieving non-linear mappings. Traditional studies mainly focus on finding fixed activations for a particular set of learning tasks or model architectures. The research on flexible activation is quite limited in both designing philosophy and application scenarios. In this study, three principles of choosing flexible activation components are proposed and a general combined form of flexible activation functions is implemented. Based on this, a novel family of flexible activation functions that can replace sigmoid or tanh in LSTM cells are implemented, as well as a new family by combining ReLU and ELUs. Also, two new regularisation terms based on assumptions as prior knowledge are introduced. It has been shown that LSTM models with proposed flexible activations P-Sig-Ramp provide significant improvements in time series forecasting, while the proposed P-E2-ReLU achieves better and more stable performance on lossy image compression tasks with convolutional auto-encoders. In addition, the proposed regularization terms improve the convergence, performance and stability of the models with flexible activation functions.

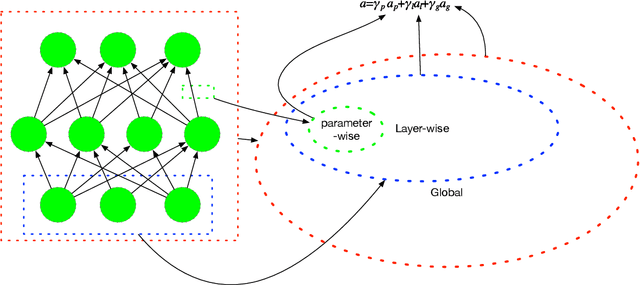
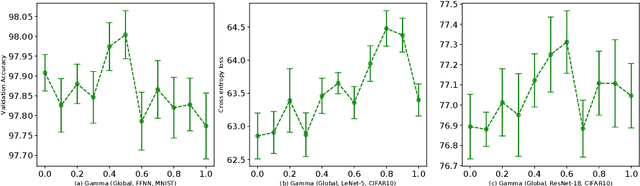
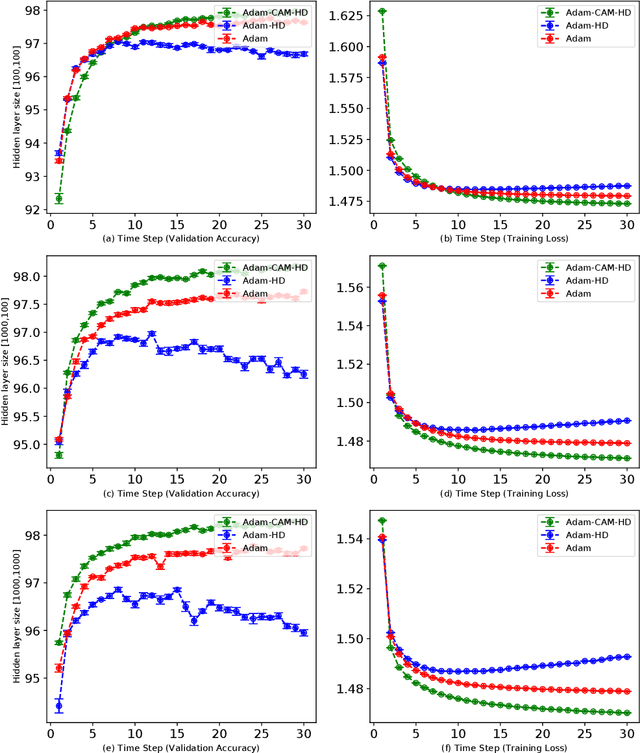
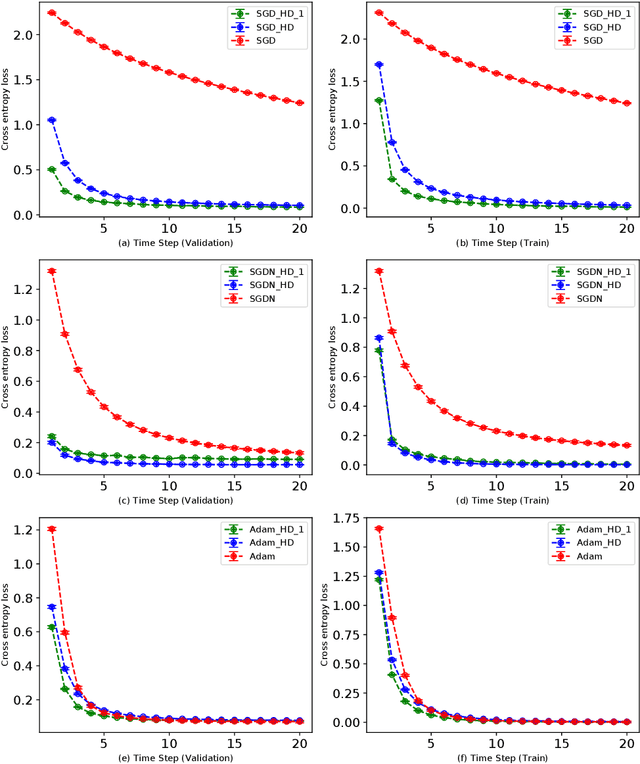
Adaptive Multi-level Hyper-gradient Descent

Adaptive learning rates can lead to faster convergence and better final performance for deep learning models. There are several widely known human-designed adaptive optimizers such as Adam and RMSProp, gradient based adaptive methods such as hyper-descent and L4, and meta learning approaches including learning to learn. However, the issue of balancing adaptiveness and over-parameterization is still a topic to be addressed. In this study, we investigate different levels of learning rate adaptation based on the framework of hyper-gradient descent, and further propose a method that adaptively learns the model parameters for combining different levels of adaptations. Meanwhile, we show the relationship between adding regularization on over-parameterized learning rates and building combinations of different levels of adaptive learning rates. The experiments on several network architectures including feed-forward networks, LeNet-5 and ResNet-34 show that the proposed multi-level adaptive approach can outperform baseline adaptive methods in a variety circumstances with statistical significance.