Boris Beranger
Logistic regression models for aggregated data
Dec 09, 2019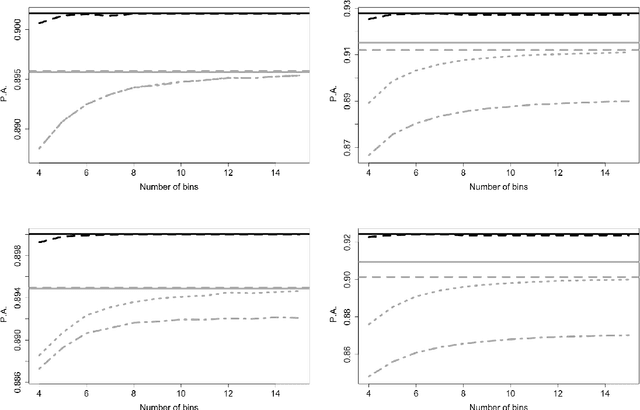
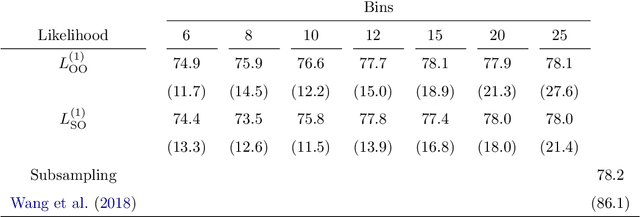
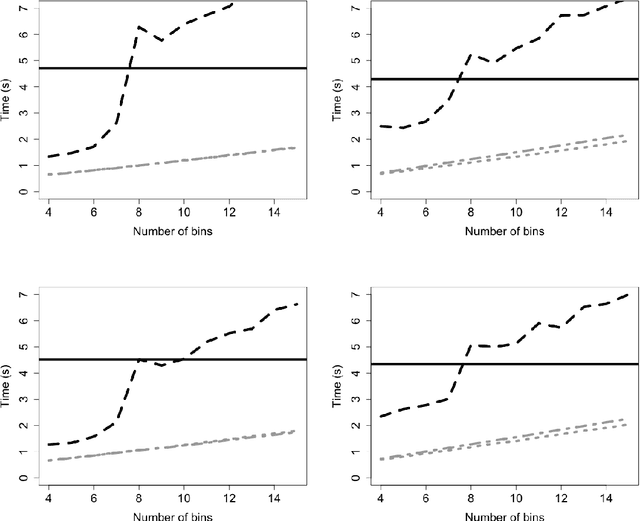
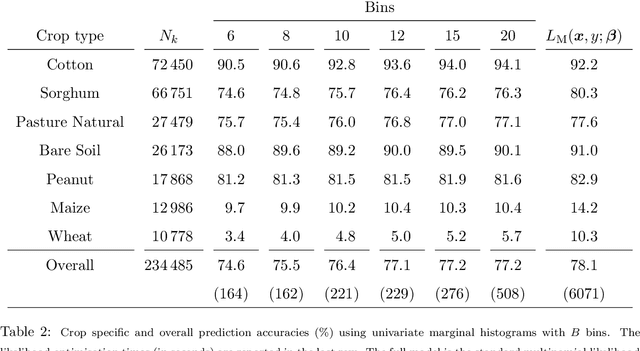
Abstract:Logistic regression models are a popular and effective method to predict the probability of categorical response data. However inference for these models can become computationally prohibitive for large datasets. Here we adapt ideas from symbolic data analysis to summarise the collection of predictor variables into histogram form, and perform inference on this summary dataset. We develop ideas based on composite likelihoods to derive an efficient one-versus-rest approximate composite likelihood model for histogram-based random variables, constructed from low-dimensional marginal histograms obtained from the full histogram. We demonstrate that this procedure can achieve comparable classification rates compared to the standard full data multinomial analysis and against state-of-the-art subsampling algorithms for logistic regression, but at a substantially lower computational cost. Performance is explored through simulated examples, and analyses of large supersymmetry and satellite crop classification datasets.
New models for symbolic data analysis
Sep 11, 2018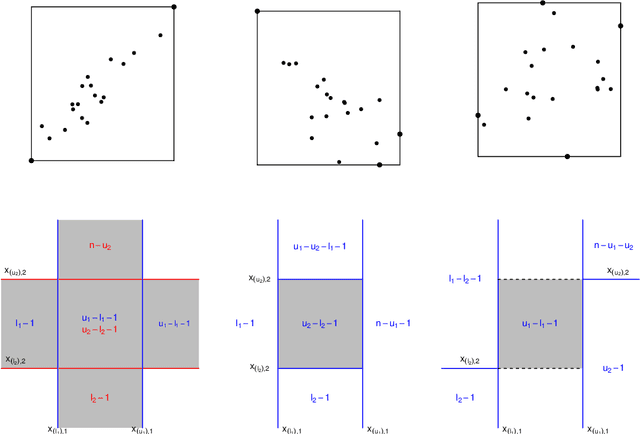
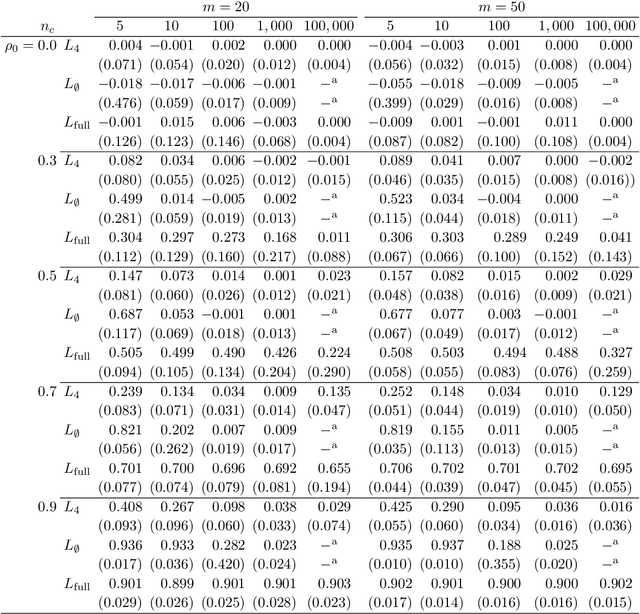
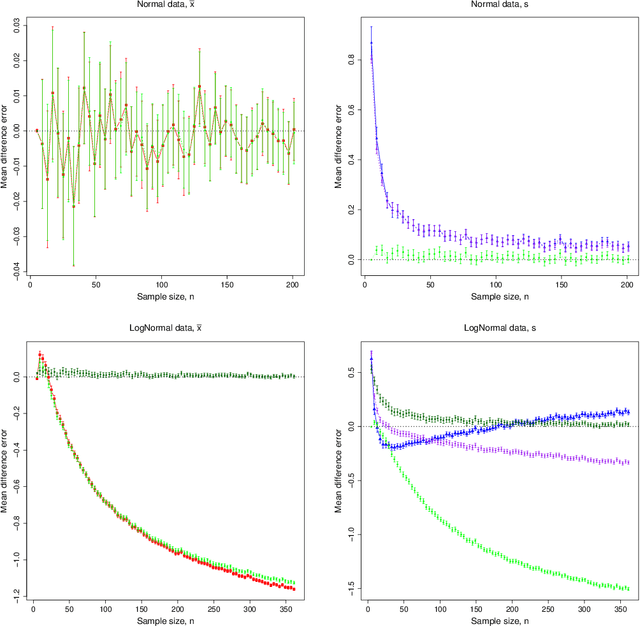
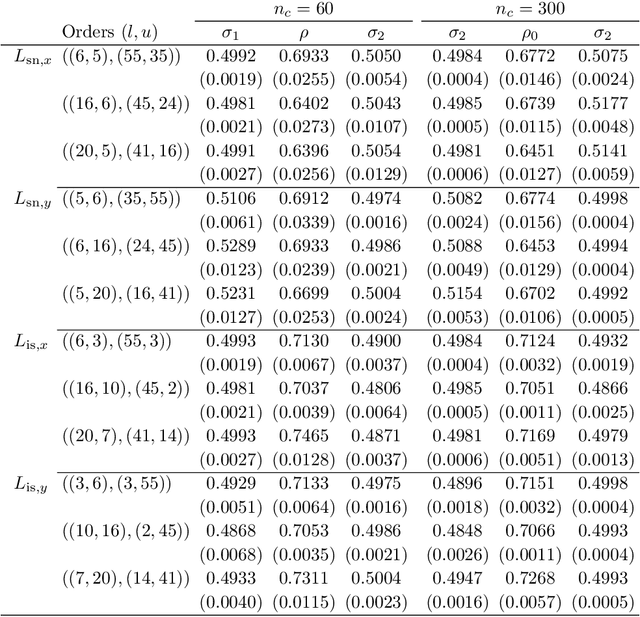
Abstract:Symbolic data analysis (SDA) is an emerging area of statistics based on aggregating individual level data into group-based distributional summaries (symbols), and then developing statistical methods to analyse them. It is ideal for analysing large and complex datasets, and has immense potential to become a standard inferential technique in the near future. However, existing SDA techniques are either non-inferential, do not easily permit meaningful statistical models, are unable to distinguish between competing models, and are based on simplifying assumptions that are known to be false. Further, the procedure for constructing symbols from the underlying data is erroneously not considered relevant to the resulting statistical analysis. In this paper we introduce a new general method for constructing likelihood functions for symbolic data based on a desired probability model for the underlying classical data, while only observing the distributional summaries. This approach resolves many of the conceptual and practical issues with current SDA methods, opens the door for new classes of symbol design and construction, in addition to developing SDA as a viable tool to enable and improve upon classical data analyses, particularly for very large and complex datasets. This work creates a new direction for SDA research, which we illustrate through several real and simulated data analyses.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge