Smoothing Graphons for Modelling Exchangeable Relational Data
Paper and Code
Feb 25, 2020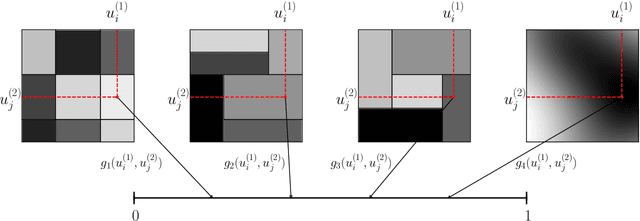
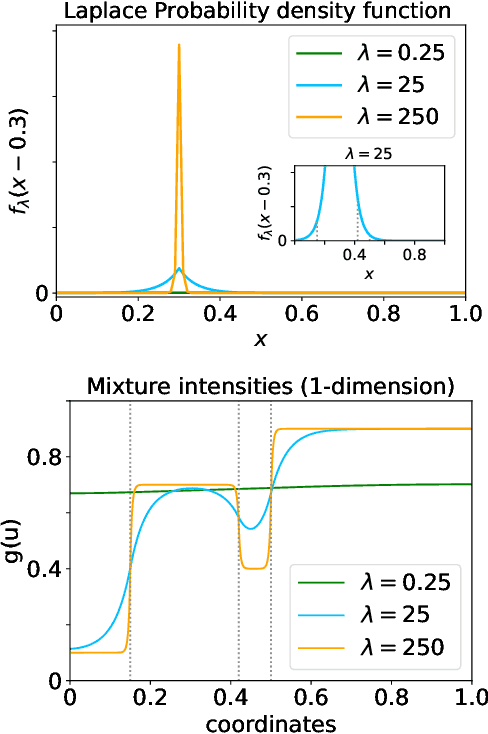

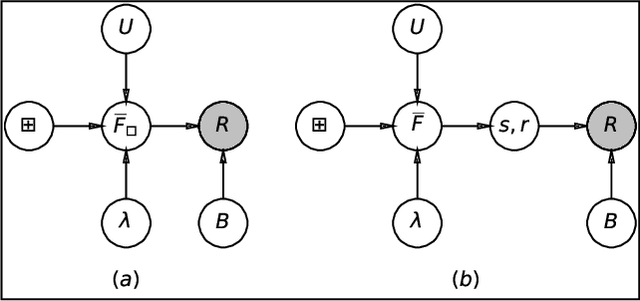
Modelling exchangeable relational data can be described by \textit{graphon theory}. Most Bayesian methods for modelling exchangeable relational data can be attributed to this framework by exploiting different forms of graphons. However, the graphons adopted by existing Bayesian methods are either piecewise-constant functions, which are insufficiently flexible for accurate modelling of the relational data, or are complicated continuous functions, which incur heavy computational costs for inference. In this work, we introduce a smoothing procedure to piecewise-constant graphons to form {\em smoothing graphons}, which permit continuous intensity values for describing relations, but without impractically increasing computational costs. In particular, we focus on the Bayesian Stochastic Block Model (SBM) and demonstrate how to adapt the piecewise-constant SBM graphon to the smoothed version. We initially propose the Integrated Smoothing Graphon (ISG) which introduces one smoothing parameter to the SBM graphon to generate continuous relational intensity values. We then develop the Latent Feature Smoothing Graphon (LFSG), which improves on the ISG by introducing auxiliary hidden labels to decompose the calculation of the ISG intensity and enable efficient inference. Experimental results on real-world data sets validate the advantages of applying smoothing strategies to the Stochastic Block Model, demonstrating that smoothing graphons can greatly improve AUC and precision for link prediction without increasing computational complexity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge