Mixtures of Gaussian process experts based on kernel stick-breaking processes

Mixtures of Gaussian process experts is a class of models that can simultaneously address two of the key limitations inherent in standard Gaussian processes: scalability and predictive performance. In particular, models that use Dirichlet processes as gating functions permit straightforward interpretation and automatic selection of the number of experts in a mixture. While the existing models are intuitive and capable of capturing non-stationarity, multi-modality and heteroskedasticity, the simplicity of their gating functions may limit the predictive performance when applied to complex data-generating processes. Capitalising on the recent advancement in the dependent Dirichlet processes literature, we propose a new mixture model of Gaussian process experts based on kernel stick-breaking processes. Our model maintains the intuitive appeal yet improve the performance of the existing models. To make it practical, we design a sampler for posterior computation based on the slice sampling. The model behaviour and improved predictive performance are demonstrated in experiments using six datasets.

Subsampling MCMC - An introduction for the survey statistician

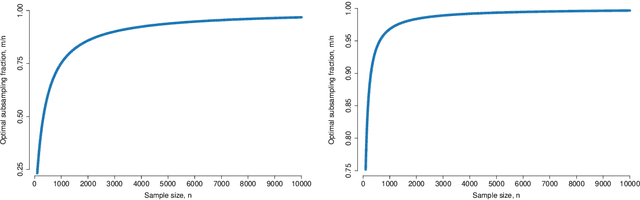
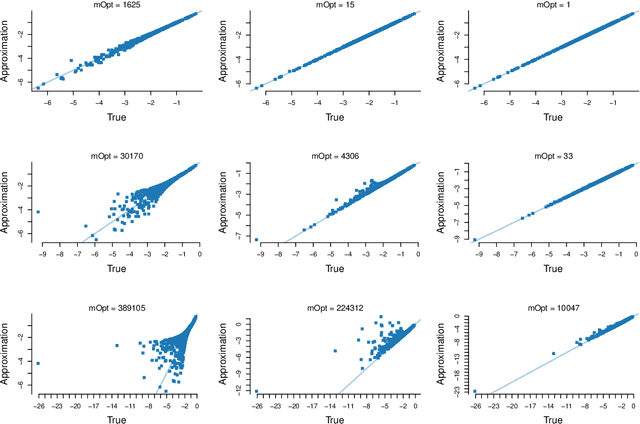
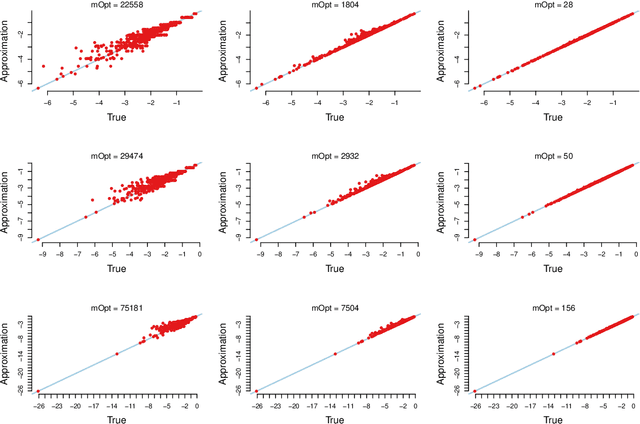
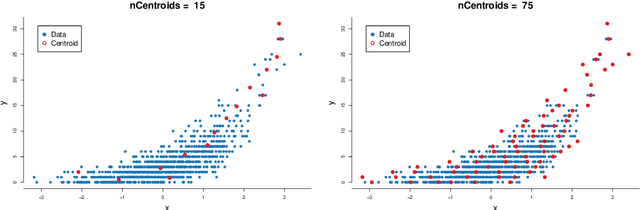
The rapid development of computing power and efficient Markov Chain Monte Carlo (MCMC) simulation algorithms have revolutionized Bayesian statistics, making it a highly practical inference method in applied work. However, MCMC algorithms tend to be computationally demanding, and are particularly slow for large datasets. Data subsampling has recently been suggested as a way to make MCMC methods scalable on massively large data, utilizing efficient sampling schemes and estimators from the survey sampling literature. These developments tend to be unknown by many survey statisticians who traditionally work with non-Bayesian methods, and rarely use MCMC. Our article explains the idea of data subsampling in MCMC by reviewing one strand of work, Subsampling MCMC, a so called pseudo-marginal MCMC approach to speeding up MCMC through data subsampling. The review is written for a survey statistician without previous knowledge of MCMC methods since our aim is to motivate survey sampling experts to contribute to the growing Subsampling MCMC literature.

Subsampling Sequential Monte Carlo for Static Bayesian Models

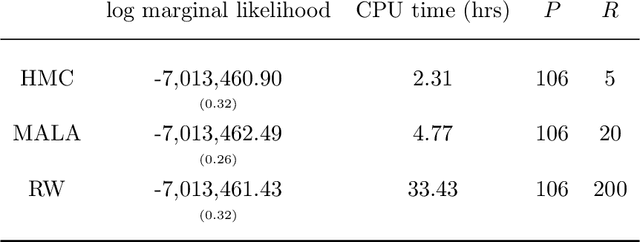
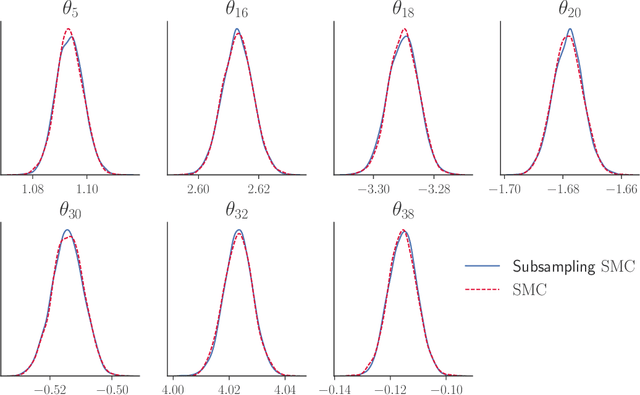
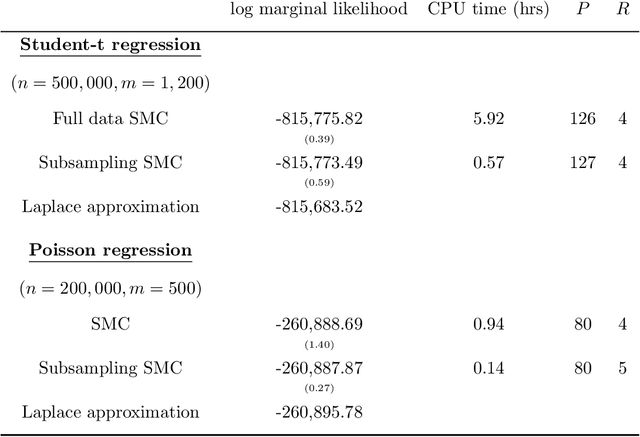
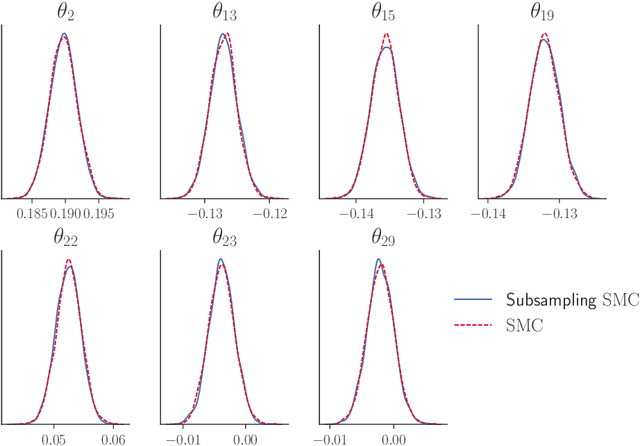
Our article shows how to carry out Bayesian inference by combining data subsampling with Sequential Monte Carlo (SMC). This takes advantage of the attractive properties of SMC for Bayesian computations with the ability of subsampling to tackle big data problems. SMC sequentially updates a cloud of particles through a sequence of densities, beginning with a density that is easy to sample from such as the prior and ending with the posterior density. Each update of the particle cloud consists of three steps: reweighting, resampling, and moving. In the move step, each particle is moved using a Markov kernel and this is typically the most computationally expensive part, particularly when the dataset is large. It is crucial to have an efficient move step to ensure particle diversity. Our article makes two important contributions. First, in order to speed up the SMC computation, we use an approximately unbiased and efficient annealed likelihood estimator based on data subsampling. The subsampling approach is more memory efficient than the corresponding full data SMC, which is a great advantage for parallel computation. Second, we use a Metropolis within Gibbs kernel with two conditional updates. First, a Hamiltonian Monte Carlo update makes distant moves for the model parameters. Second, a block pseudo-marginal proposal is used for the particles corresponding to the auxiliary variables for the data subsampling. We demonstrate the usefulness of the methodology using two large datasets.

The block-Poisson estimator for optimally tuned exact subsampling MCMC

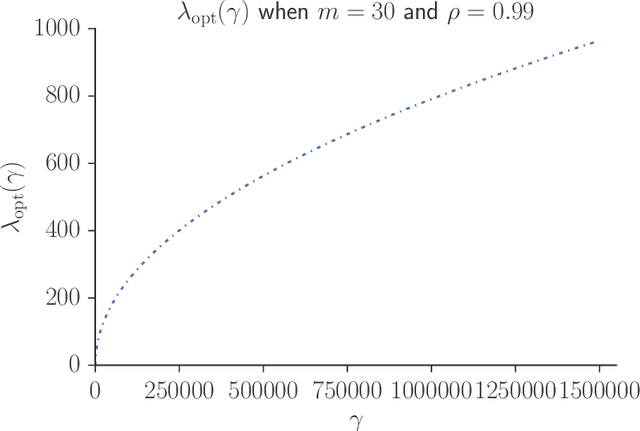
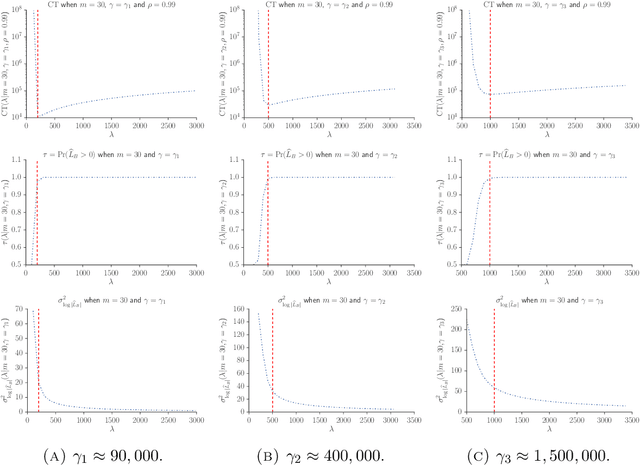
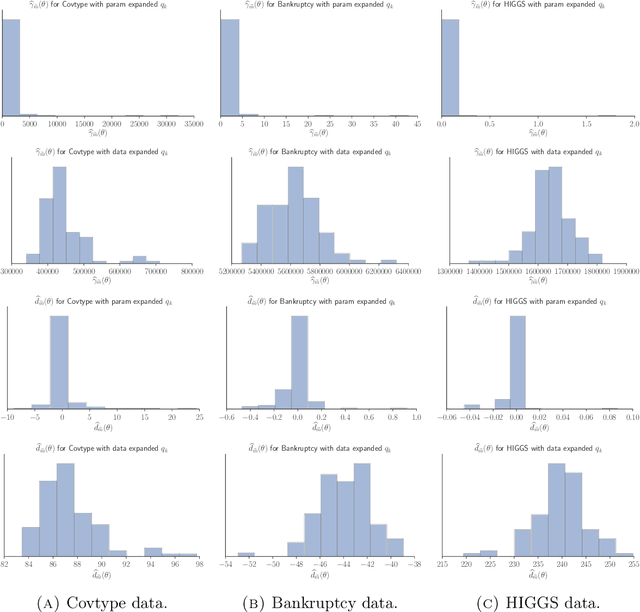
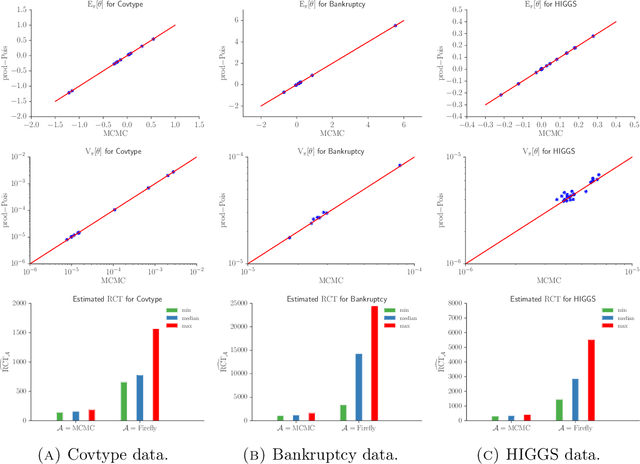
Speeding up Markov Chain Monte Carlo (MCMC) for datasets with many observations by data subsampling has recently received considerable attention in the literature. The currently available methods are either approximate, highly inefficient or limited to small dimensional models. We propose a pseudo-marginal MCMC method that estimates the likelihood by data subsampling using a block-Poisson estimator. The estimator is a product of Poisson estimators, each based on an independent subset of the observations. The construction allows us to update a subset of the blocks in each MCMC iteration, thereby inducing a controllable correlation between the estimates at the current and proposed draw in the Metropolis-Hastings ratio. This makes it possible to use highly variable likelihood estimators without adversely affecting the sampling efficiency. Poisson estimators are unbiased but not necessarily positive. We therefore follow Lyne et al. (2015) and run the MCMC on the absolute value of the estimator and use an importance sampling correction for occasionally negative likelihood estimates to estimate expectations of any function of the parameters. We provide analytically derived guidelines to select the optimal tuning parameters for the algorithm by minimizing the variance of the importance sampling corrected estimator per unit of computing time. The guidelines are derived under idealized conditions, but are demonstrated to be quite accurate in empirical experiments. The guidelines apply to any pseudo-marginal algorithm if the likelihood is estimated by the block-Poisson estimator, including the class of doubly intractable problems in Lyne et al. (2015). We illustrate the method in a logistic regression example and find dramatic improvements compared to regular MCMC without subsampling and a popular exact subsampling approach recently proposed in the literature.

Hamiltonian Monte Carlo with Energy Conserving Subsampling

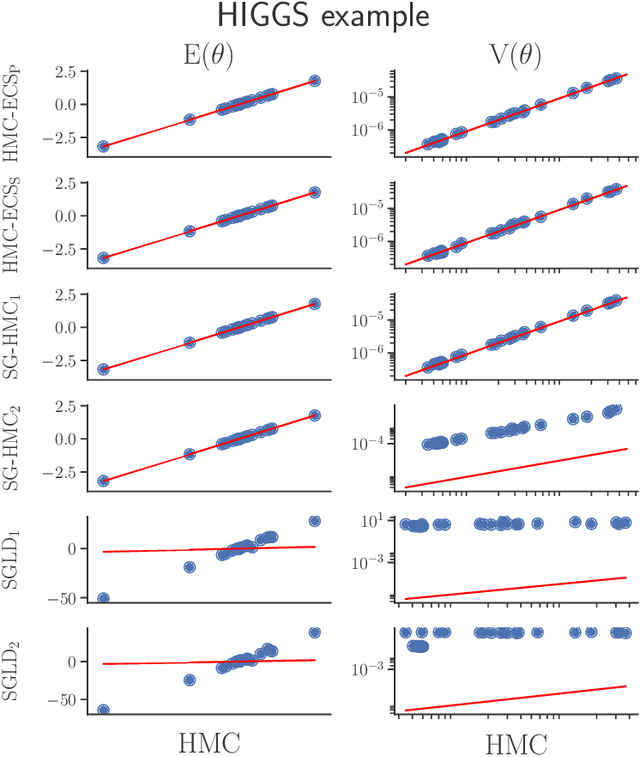
Hamiltonian Monte Carlo (HMC) has recently received considerable attention in the literature due to its ability to overcome the slow exploration of the parameter space inherent in random walk proposals. In tandem, data subsampling has been extensively used to overcome the computational bottlenecks in posterior sampling algorithms that require evaluating the likelihood over the whole data set, or its gradient. However, while data subsampling has been successful in traditional MCMC algorithms such as Metropolis-Hastings, it has been demonstrated to be unsuccessful in the context of HMC, both in terms of poor sampling efficiency and in producing highly biased inferences. We propose an efficient HMC-within-Gibbs algorithm that utilizes data subsampling to speed up computations and simulates from a slightly perturbed target, which is within $O(m^{-2})$ of the true target, where $m$ is the size of the subsample. We also show how to modify the method to obtain exact inference on any function of the parameters. Contrary to previous unsuccessful approaches, we perform subsampling in a way that conserves energy but for a modified Hamiltonian. We can therefore maintain high acceptance rates even for distant proposals. We apply the method for simulating from the posterior distribution of a high-dimensional spline model for bankruptcy data and document speed ups of several orders of magnitude compare to standard HMC and, moreover, demonstrate a negligible bias.