The block-Poisson estimator for optimally tuned exact subsampling MCMC

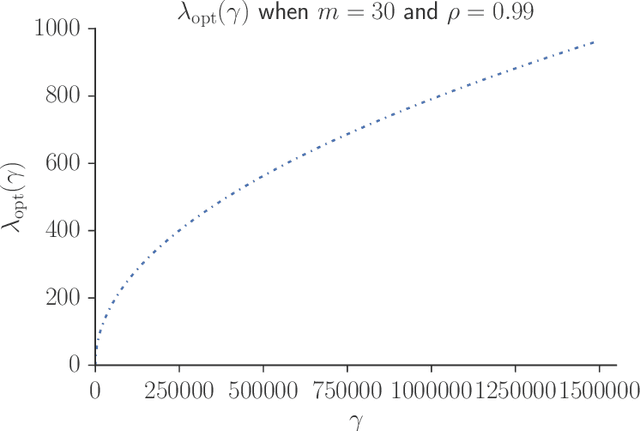
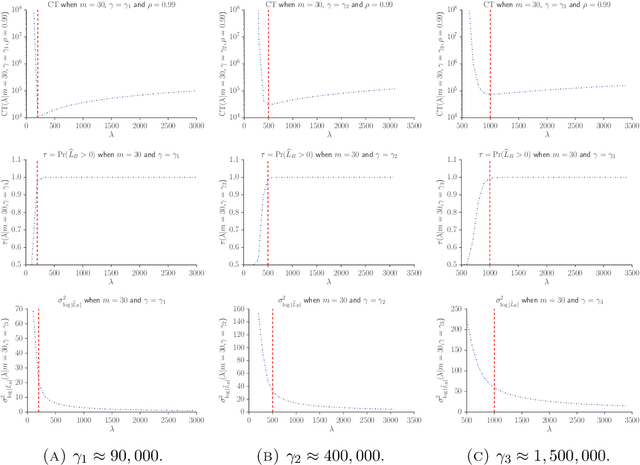
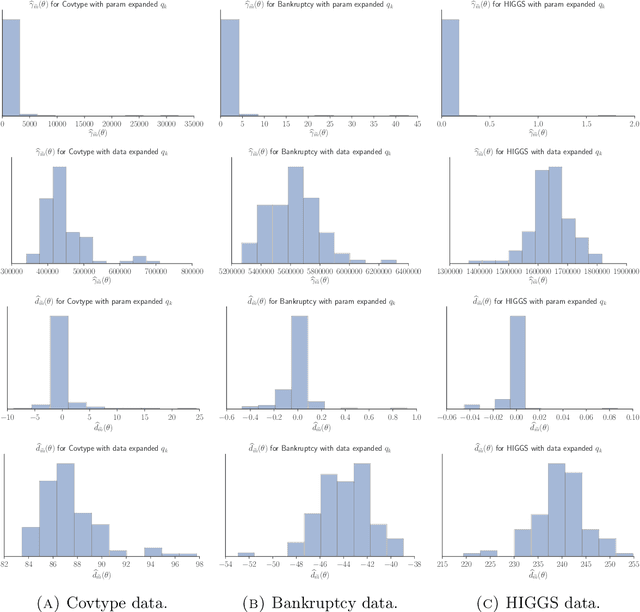
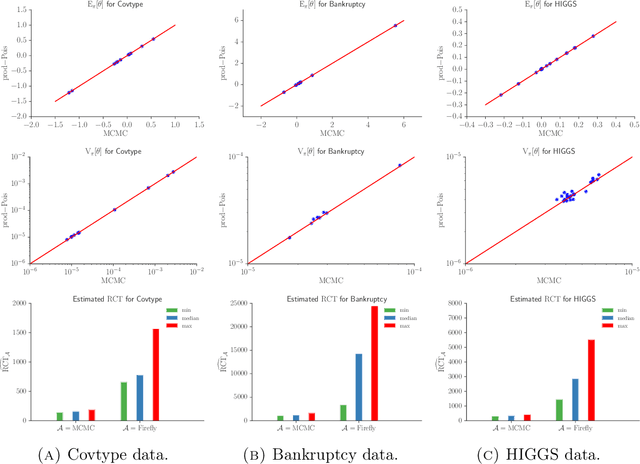
Speeding up Markov Chain Monte Carlo (MCMC) for datasets with many observations by data subsampling has recently received considerable attention in the literature. The currently available methods are either approximate, highly inefficient or limited to small dimensional models. We propose a pseudo-marginal MCMC method that estimates the likelihood by data subsampling using a block-Poisson estimator. The estimator is a product of Poisson estimators, each based on an independent subset of the observations. The construction allows us to update a subset of the blocks in each MCMC iteration, thereby inducing a controllable correlation between the estimates at the current and proposed draw in the Metropolis-Hastings ratio. This makes it possible to use highly variable likelihood estimators without adversely affecting the sampling efficiency. Poisson estimators are unbiased but not necessarily positive. We therefore follow Lyne et al. (2015) and run the MCMC on the absolute value of the estimator and use an importance sampling correction for occasionally negative likelihood estimates to estimate expectations of any function of the parameters. We provide analytically derived guidelines to select the optimal tuning parameters for the algorithm by minimizing the variance of the importance sampling corrected estimator per unit of computing time. The guidelines are derived under idealized conditions, but are demonstrated to be quite accurate in empirical experiments. The guidelines apply to any pseudo-marginal algorithm if the likelihood is estimated by the block-Poisson estimator, including the class of doubly intractable problems in Lyne et al. (2015). We illustrate the method in a logistic regression example and find dramatic improvements compared to regular MCMC without subsampling and a popular exact subsampling approach recently proposed in the literature.