On Partial Prototype Collapse in the DINO Family of Self-Supervised Methods

A prominent self-supervised learning paradigm is to model the representations as clusters, or more generally as a mixture model. Learning to map the data samples to compact representations and fitting the mixture model simultaneously leads to the representation collapse problem. Regularizing the distribution of data points over the clusters is the prevalent strategy to avoid this issue. While this is sufficient to prevent full representation collapse, we show that a partial prototype collapse problem still exists in the DINO family of methods, that leads to significant redundancies in the prototypes. Such prototype redundancies serve as shortcuts for the method to achieve a marginal latent class distribution that matches the prescribed prior. We show that by encouraging the model to use diverse prototypes, the partial prototype collapse can be mitigated. Effective utilization of the prototypes enables the methods to learn more fine-grained clusters, encouraging more informative representations. We demonstrate that this is especially beneficial when pre-training on a long-tailed fine-grained dataset.

DINO as a von Mises-Fisher mixture model

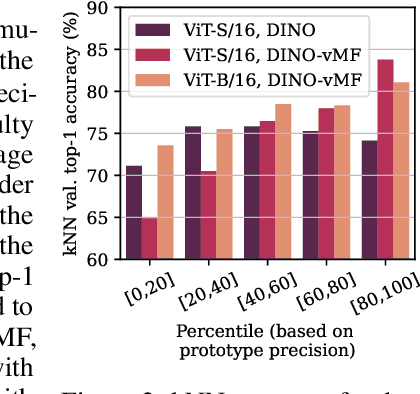
Self-distillation methods using Siamese networks are popular for self-supervised pre-training. DINO is one such method based on a cross-entropy loss between $K$-dimensional probability vectors, obtained by applying a softmax function to the dot product between representations and learnt prototypes. Given the fact that the learned representations are $L^2$-normalized, we show that DINO and its derivatives, such as iBOT, can be interpreted as a mixture model of von Mises-Fisher components. With this interpretation, DINO assumes equal precision for all components when the prototypes are also $L^2$-normalized. Using this insight we propose DINO-vMF, that adds appropriate normalization constants when computing the cluster assignment probabilities. Unlike DINO, DINO-vMF is stable also for the larger ViT-Base model with unnormalized prototypes. We show that the added flexibility of the mixture model is beneficial in terms of better image representations. The DINO-vMF pre-trained model consistently performs better than DINO on a range of downstream tasks. We obtain similar improvements for iBOT-vMF vs iBOT and thereby show the relevance of our proposed modification also for other methods derived from DINO.

Temporal Graph Neural Networks for Irregular Data

This paper proposes a temporal graph neural network model for forecasting of graph-structured irregularly observed time series. Our TGNN4I model is designed to handle both irregular time steps and partial observations of the graph. This is achieved by introducing a time-continuous latent state in each node, following a linear Ordinary Differential Equation (ODE) defined by the output of a Gated Recurrent Unit (GRU). The ODE has an explicit solution as a combination of exponential decay and periodic dynamics. Observations in the graph neighborhood are taken into account by integrating graph neural network layers in both the GRU state update and predictive model. The time-continuous dynamics additionally enable the model to make predictions at arbitrary time steps. We propose a loss function that leverages this and allows for training the model for forecasting over different time horizons. Experiments on simulated data and real-world data from traffic and climate modeling validate the usefulness of both the graph structure and time-continuous dynamics in settings with irregular observations.

Scalable Deep Gaussian Markov Random Fields for General Graphs

Machine learning methods on graphs have proven useful in many applications due to their ability to handle generally structured data. The framework of Gaussian Markov Random Fields (GMRFs) provides a principled way to define Gaussian models on graphs by utilizing their sparsity structure. We propose a flexible GMRF model for general graphs built on the multi-layer structure of Deep GMRFs, originally proposed for lattice graphs only. By designing a new type of layer we enable the model to scale to large graphs. The layer is constructed to allow for efficient training using variational inference and existing software frameworks for Graph Neural Networks. For a Gaussian likelihood, close to exact Bayesian inference is available for the latent field. This allows for making predictions with accompanying uncertainty estimates. The usefulness of the proposed model is verified by experiments on a number of synthetic and real world datasets, where it compares favorably to other both Bayesian and deep learning methods.

Deep Gaussian Markov random fields

Gaussian Markov random fields (GMRFs) are probabilistic graphical models widely used in spatial statistics and related fields to model dependencies over spatial structures. We establish a formal connection between GMRFs and convolutional neural networks (CNNs). Common GMRFs are special cases of a generative model where the inverse mapping from data to latent variables is given by a 1-layer linear CNN. This connection allows us to generalize GMRFs to multi-layer CNN architectures, effectively increasing the order of the corresponding GMRF in a way which has favorable computational scaling. We describe how well-established tools, such as autodiff and variational inference, can be used for simple and efficient inference and learning of the deep GMRF. We demonstrate the flexibility of the proposed model and show that it outperforms the state-of-the-art on a dataset of satellite temperatures, in terms of prediction and predictive uncertainty.

Real-Time Robotic Search using Hierarchical Spatial Point Processes

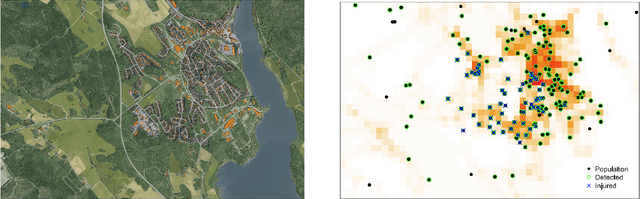
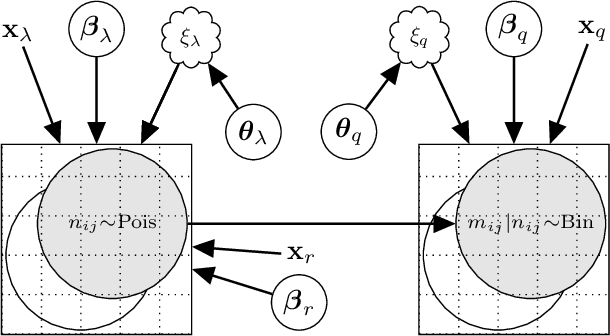
Aerial robots hold great potential for aiding Search and Rescue (SAR) efforts over large areas. Traditional approaches typically searches an area exhaustively, thereby ignoring that the density of victims varies based on predictable factors, such as the terrain, population density and the type of disaster. We present a probabilistic model to automate SAR planning, with explicit minimization of the expected time to discovery. The proposed model is a hierarchical spatial point process with three interacting spatial fields for i) the point patterns of persons in the area, ii) the probability of detecting persons and iii) the probability of injury. This structure allows inclusion of informative priors from e.g. geographic or cell phone traffic data, while falling back to latent Gaussian processes when priors are missing or inaccurate. To solve this problem in real-time, we propose a combination of fast approximate inference using Integrated Nested Laplace Approximation (INLA), and a novel Monte Carlo tree search tailored to the problem. Experiments using data simulated from real world GIS maps show that the framework outperforms traditional search strategies, and finds up to ten times more injured in the crucial first hours.