Speeding Up MCMC by Efficient Data Subsampling
Paper and Code
Jan 01, 2018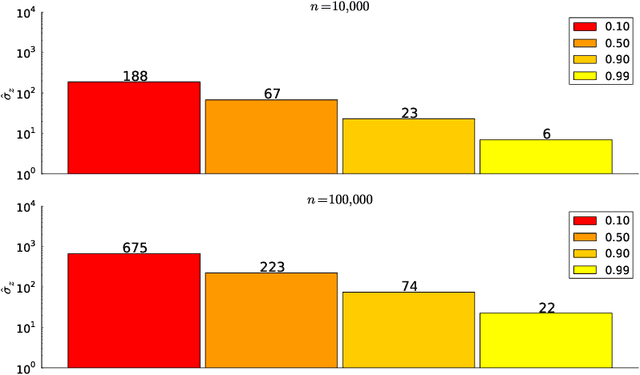
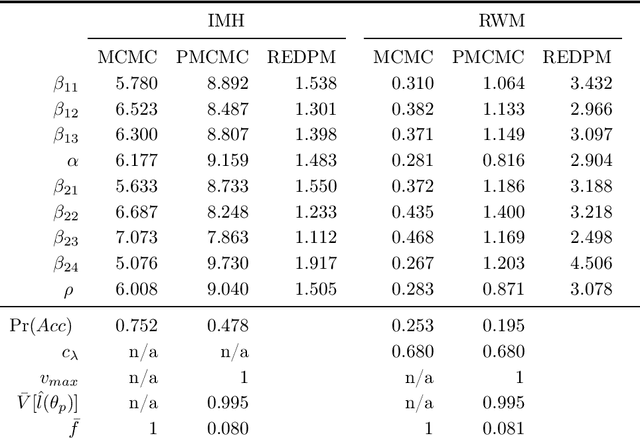
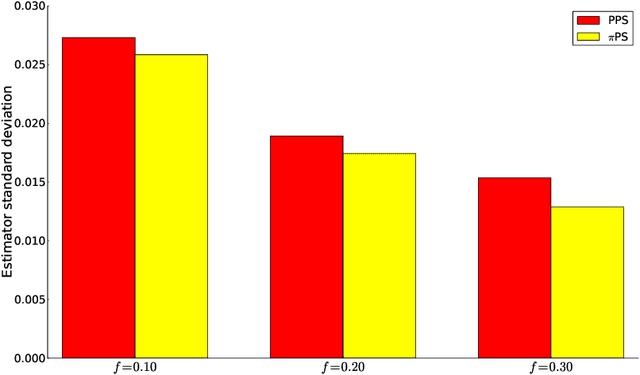

We propose Subsampling MCMC, a Markov Chain Monte Carlo (MCMC) framework where the likelihood function for $n$ observations is estimated from a random subset of $m$ observations. We introduce a highly efficient unbiased estimator of the log-likelihood based on control variates, such that the computing cost is much smaller than that of the full log-likelihood in standard MCMC. The likelihood estimate is bias-corrected and used in two dependent pseudo-marginal algorithms to sample from a perturbed posterior, for which we derive the asymptotic error with respect to $n$ and $m$, respectively. We propose a practical estimator of the error and show that the error is negligible even for a very small $m$ in our applications. We demonstrate that Subsampling MCMC is substantially more efficient than standard MCMC in terms of sampling efficiency for a given computational budget, and that it outperforms other subsampling methods for MCMC proposed in the literature.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge