Bayesian optimisation for fast approximate inference in state-space models with intractable likelihoods
Paper and Code
Jun 13, 2017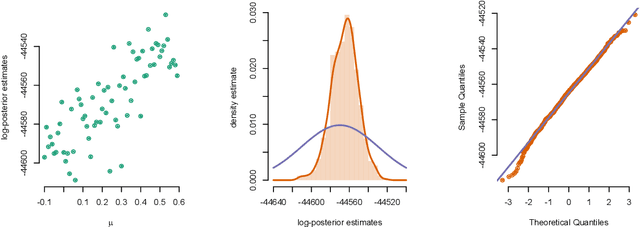
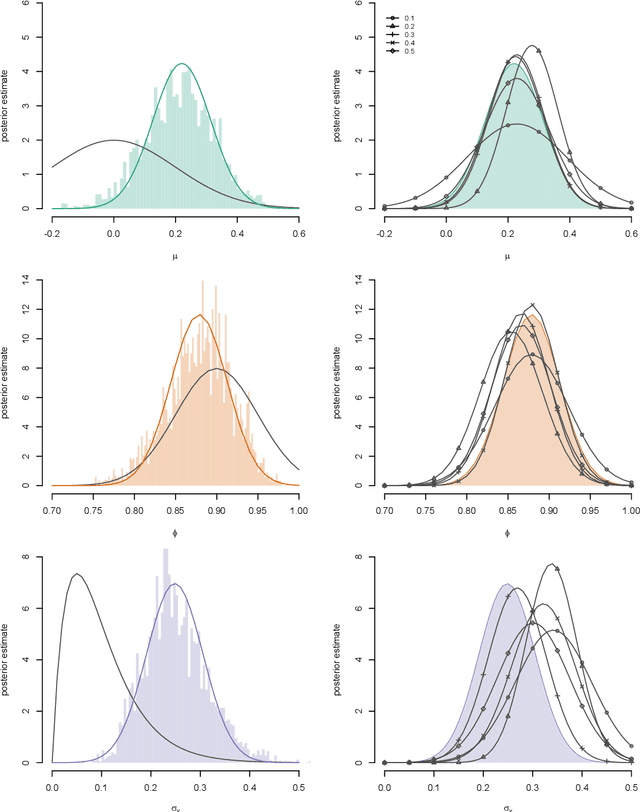
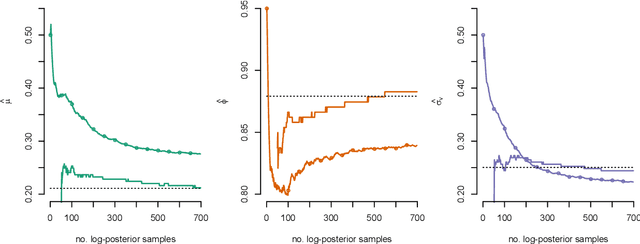
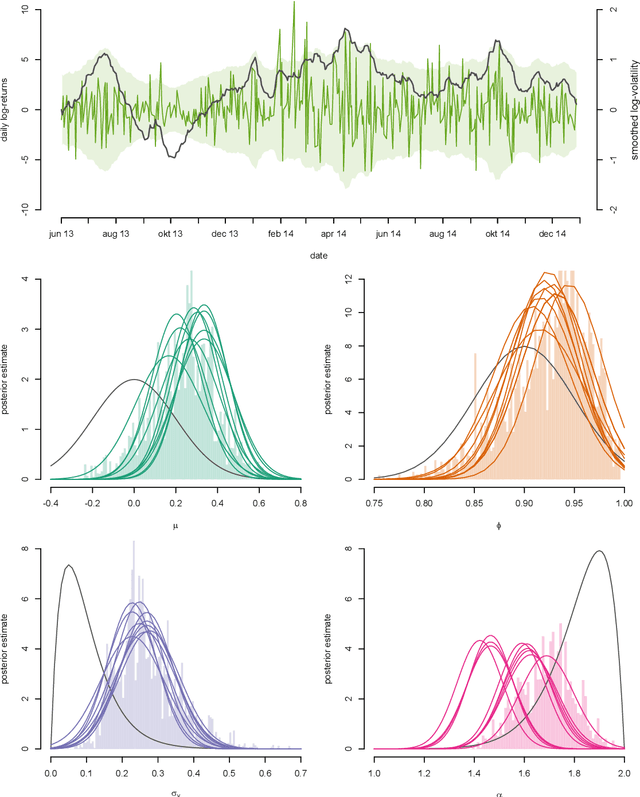
We consider the problem of approximate Bayesian parameter inference in non-linear state-space models with intractable likelihoods. Sequential Monte Carlo with approximate Bayesian computations (SMC-ABC) is one approach to approximate the likelihood in this type of models. However, such approximations can be noisy and computationally costly which hinders efficient implementations using standard methods based on optimisation and Monte Carlo methods. We propose a computationally efficient novel method based on the combination of Gaussian process optimisation and SMC-ABC to create a Laplace approximation of the intractable posterior. We exemplify the proposed algorithm for inference in stochastic volatility models with both synthetic and real-world data as well as for estimating the Value-at-Risk for two portfolios using a copula model. We document speed-ups of between one and two orders of magnitude compared to state-of-the-art algorithms for posterior inference.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge