Variational State and Parameter Estimation

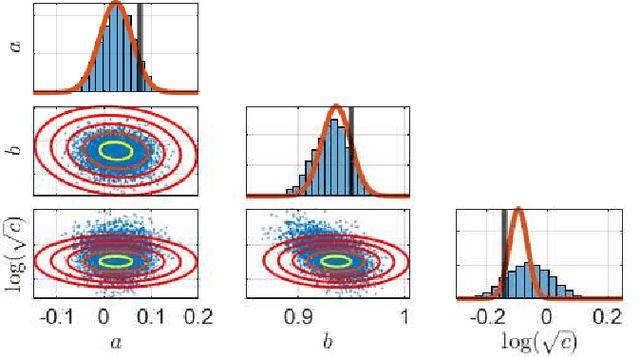
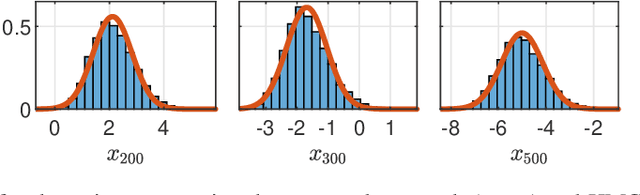
This paper considers the problem of computing Bayesian estimates of both states and model parameters for nonlinear state-space models. Generally, this problem does not have a tractable solution and approximations must be utilised. In this work, a variational approach is used to provide an assumed density which approximates the desired, intractable, distribution. The approach is deterministic and results in an optimisation problem of a standard form. Due to the parametrisation of the assumed density selected first- and second-order derivatives are readily available which allows for efficient solutions. The proposed method is compared against state-of-the-art Hamiltonian Monte Carlo in two numerical examples.

Variational Nonlinear System Identification

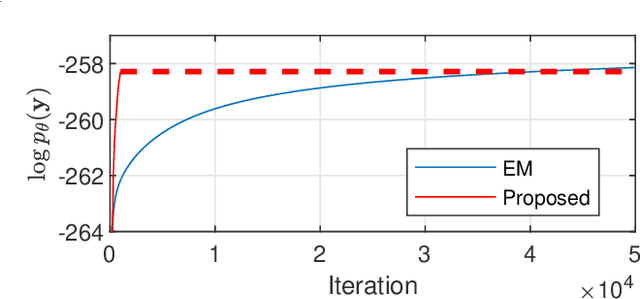
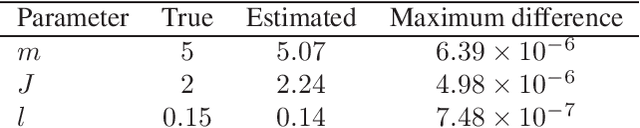
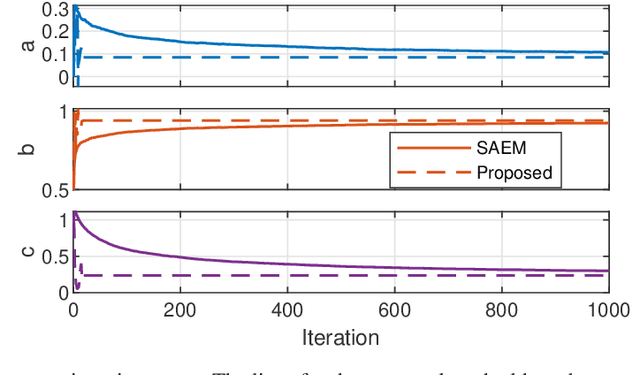
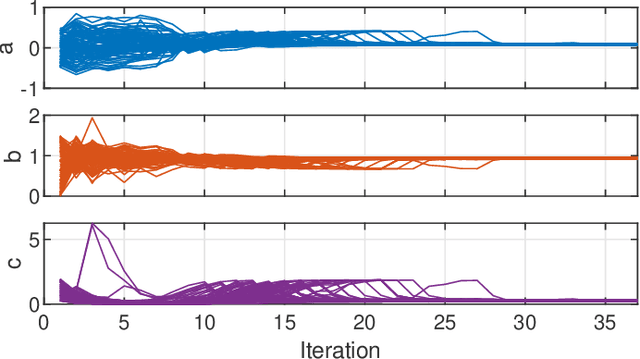
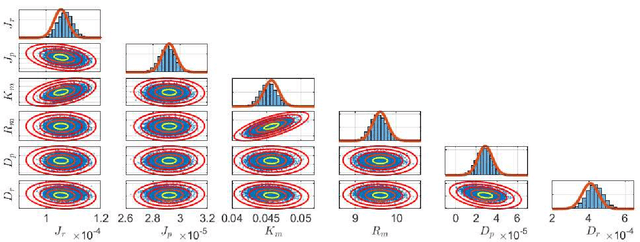
This paper considers parameter estimation for nonlinear state-space models, which is an important but challenging problem. We address this challenge by employing a variational inference (VI) approach, which is a principled method that has deep connections to maximum likelihood estimation. This VI approach ultimately provides estimates of the model as solutions to an optimisation problem, which is deterministic, tractable and can be solved using standard optimisation tools. A specialisation of this approach for systems with additive Gaussian noise is also detailed. The proposed method is examined numerically on a range of simulation and real examples with a focus on robustness to parameter initialisations; we additionally perform favourable comparisons against state-of-the-art alternatives.

Correlated pseudo-marginal Metropolis-Hastings using quasi-Newton proposals

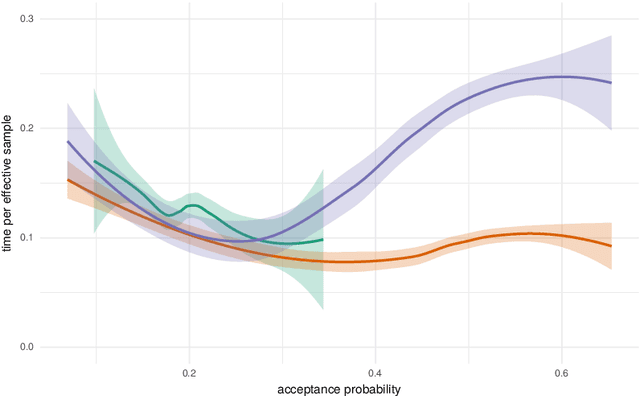
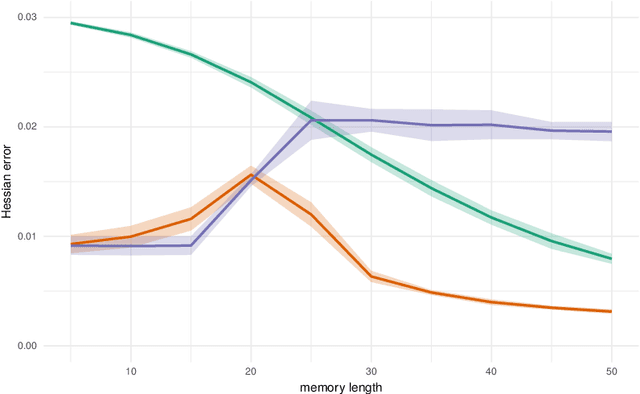
Pseudo-marginal Metropolis-Hastings (pmMH) is a versatile algorithm for sampling from target distributions which are not easy to evaluate point-wise. However, pmMH requires good proposal distributions to sample efficiently from the target, which can be problematic to construct in practice. This is especially a problem for high-dimensional targets when the standard random-walk proposal is inefficient. We extend pmMH to allow for constructing the proposal based on information from multiple past iterations. As a consequence, quasi-Newton (qN) methods can be employed to form proposals which utilize gradient information to guide the Markov chain to areas of high probability and to construct approximations of the local curvature to scale step sizes. The proposed method is demonstrated on several problems which indicate that qN proposals can perform better than other common Hessian-based proposals.

A Bayesian Filtering Algorithm for Gaussian Mixture Models

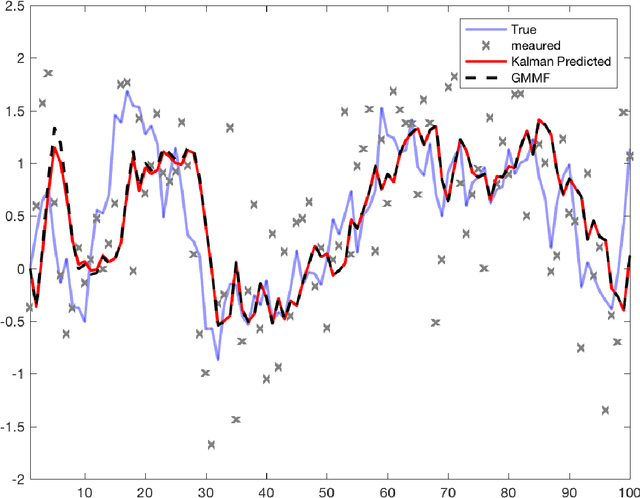
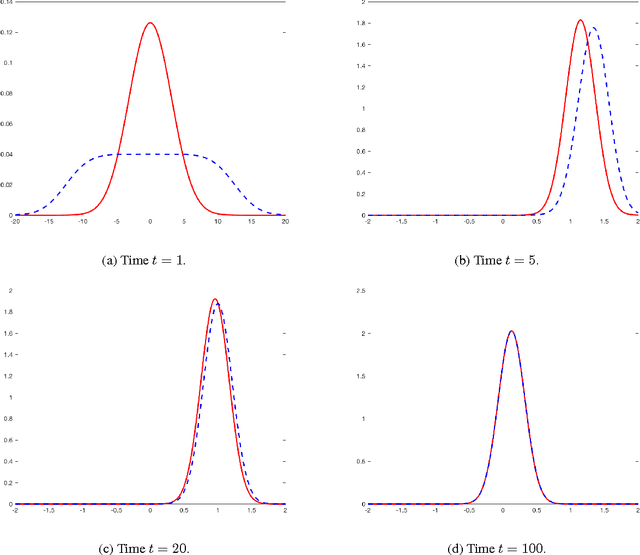
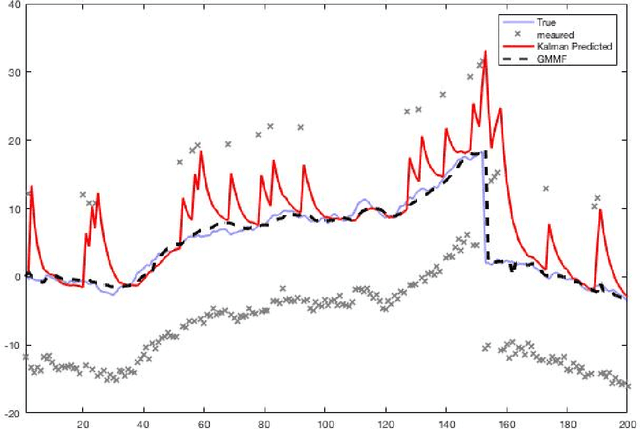
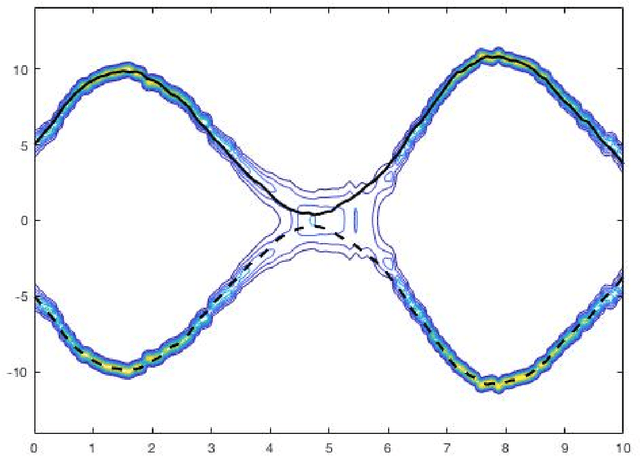
A Bayesian filtering algorithm is developed for a class of state-space systems that can be modelled via Gaussian mixtures. In general, the exact solution to this filtering problem involves an exponential growth in the number of mixture terms and this is handled here by utilising a Gaussian mixture reduction step after both the time and measurement updates. In addition, a square-root implementation of the unified algorithm is presented and this algorithm is profiled on several simulated systems. This includes the state estimation for two non-linear systems that are strictly outside the class considered in this paper.