A Probabilistically Motivated Learning Rate Adaptation for Stochastic Optimization

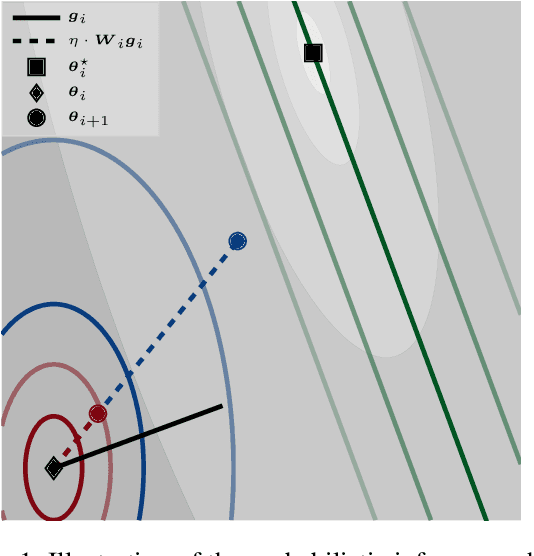
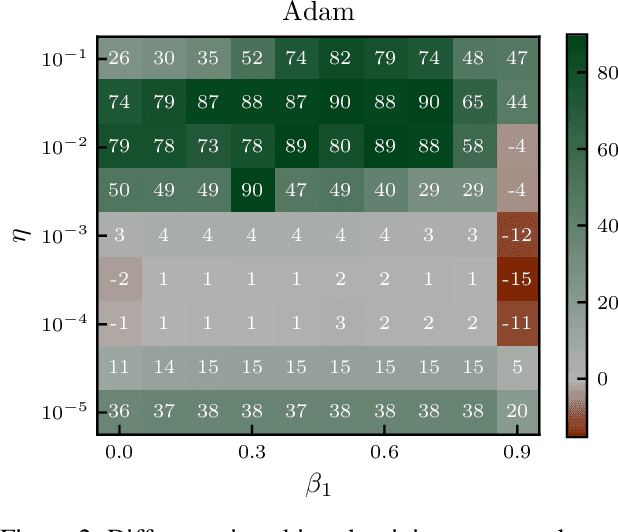
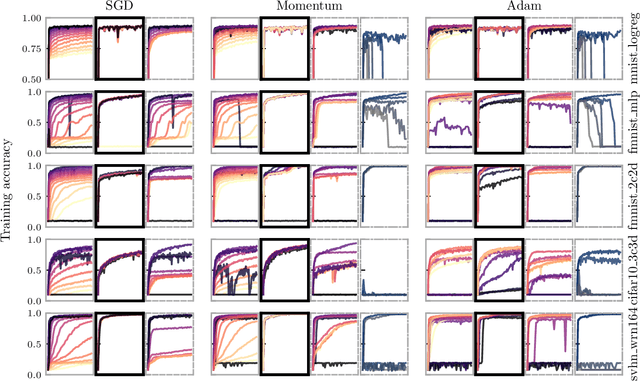
Machine learning practitioners invest significant manual and computational resources in finding suitable learning rates for optimization algorithms. We provide a probabilistic motivation, in terms of Gaussian inference, for popular stochastic first-order methods. As an important special case, it recovers the Polyak step with a general metric. The inference allows us to relate the learning rate to a dimensionless quantity that can be automatically adapted during training by a control algorithm. The resulting meta-algorithm is shown to adapt learning rates in a robust manner across a large range of initial values when applied to deep learning benchmark problems.

Variational State and Parameter Estimation

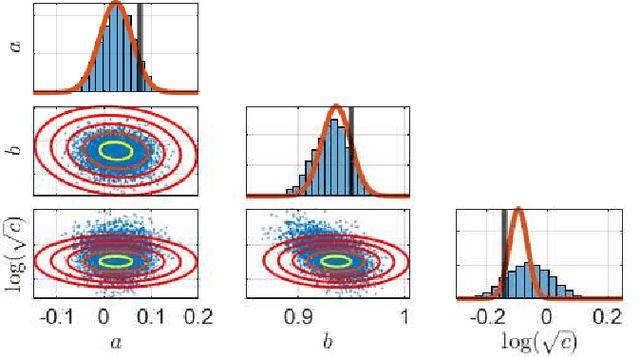
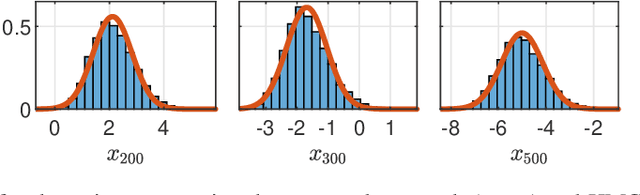
This paper considers the problem of computing Bayesian estimates of both states and model parameters for nonlinear state-space models. Generally, this problem does not have a tractable solution and approximations must be utilised. In this work, a variational approach is used to provide an assumed density which approximates the desired, intractable, distribution. The approach is deterministic and results in an optimisation problem of a standard form. Due to the parametrisation of the assumed density selected first- and second-order derivatives are readily available which allows for efficient solutions. The proposed method is compared against state-of-the-art Hamiltonian Monte Carlo in two numerical examples.

Variational Nonlinear System Identification

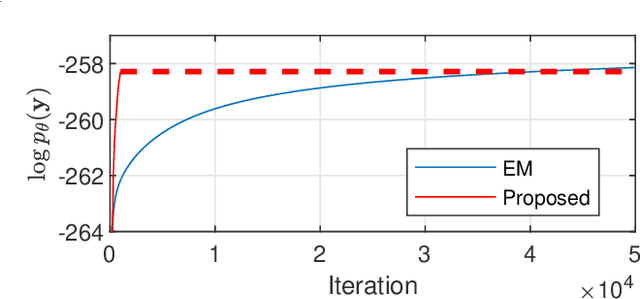
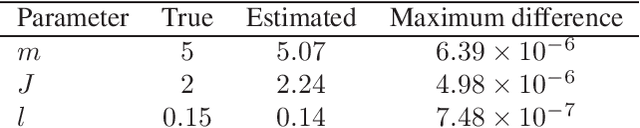
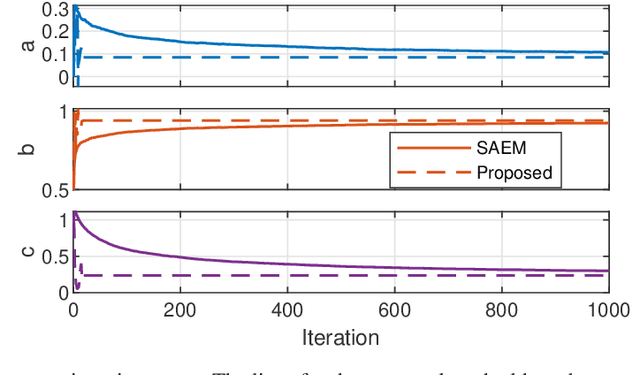
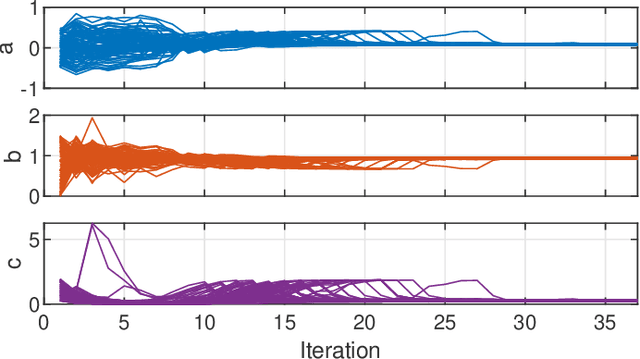
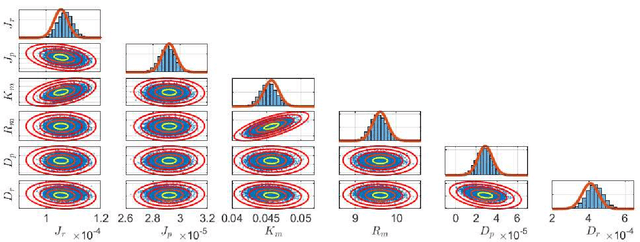
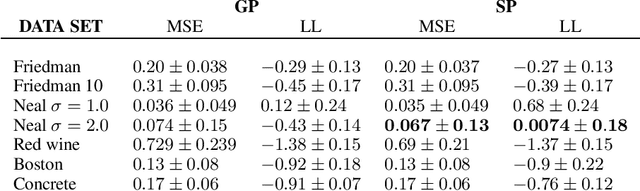
This paper considers parameter estimation for nonlinear state-space models, which is an important but challenging problem. We address this challenge by employing a variational inference (VI) approach, which is a principled method that has deep connections to maximum likelihood estimation. This VI approach ultimately provides estimates of the model as solutions to an optimisation problem, which is deterministic, tractable and can be solved using standard optimisation tools. A specialisation of this approach for systems with additive Gaussian noise is also detailed. The proposed method is examined numerically on a range of simulation and real examples with a focus on robustness to parameter initialisations; we additionally perform favourable comparisons against state-of-the-art alternatives.

The Elliptical Processes: a New Family of Flexible Stochastic Processes

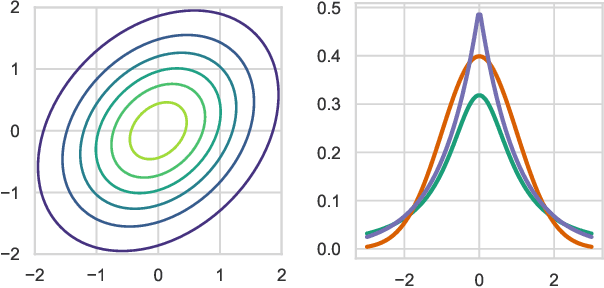
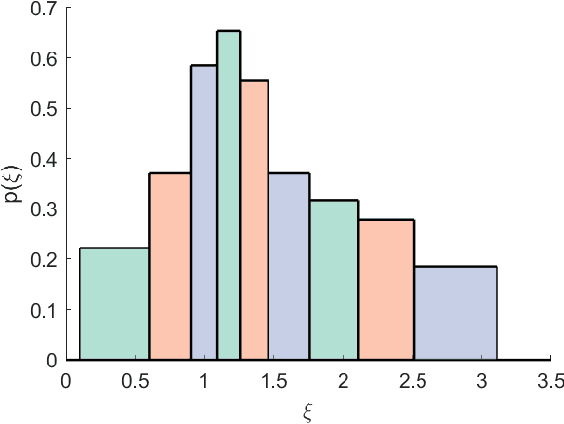
We present the elliptical processes-a new family of stochastic processes that subsumes the Gaussian process and the Student-t process. This generalization retains computational tractability while substantially increasing the range of tail behaviors that can be modeled. We base the elliptical processes on a representation of elliptical distributions as mixtures of Gaussian distributions and derive closed-form expressions for the marginal and conditional distributions. We perform an in-depth study of a particular elliptical process, where the mixture distribution is piecewise constant, and show some of its advantages over the Gaussian process through a number of experiments on robust regression. Looking forward, we believe there are several settings, e.g. when the likelihood is not Gaussian or when accurate tail modeling is critical, where the elliptical processes could become the stochastic processes of choice.

Linearly Constrained Neural Networks

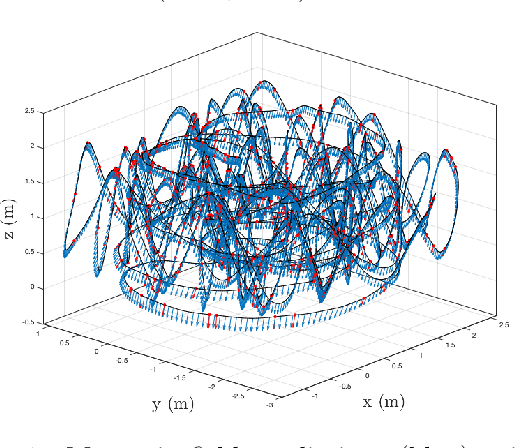
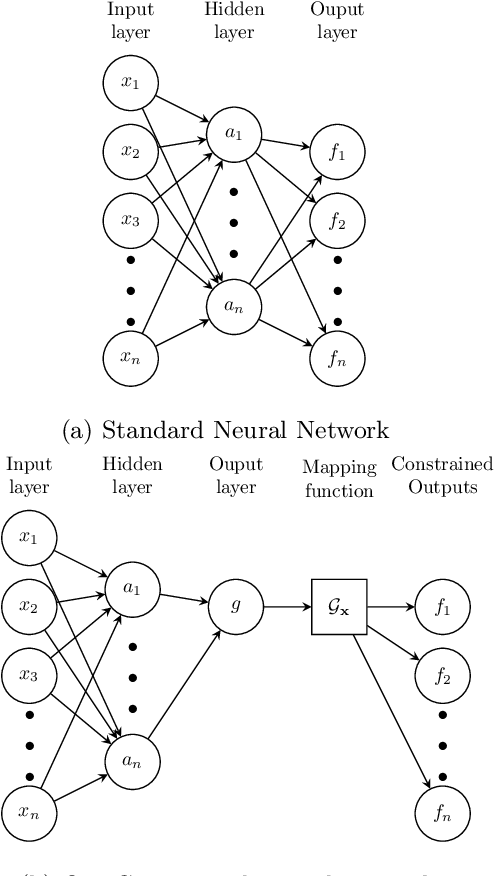
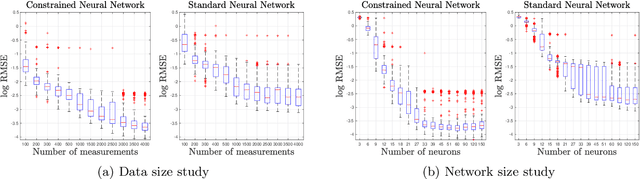
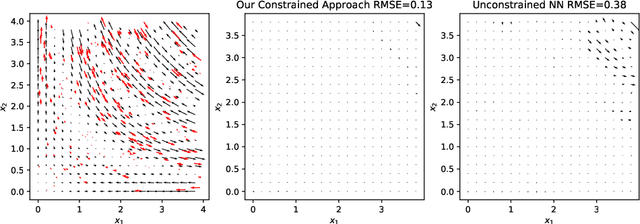
We present an approach to designing neural network based models that will explicitly satisfy known linear constraints. To achieve this, the target function is modelled as a linear transformation of an underlying function. This transformation is chosen such that any prediction of the target function is guaranteed to satisfy the constraints and can be determined from known physics or, more generally, by following a constructive procedure that was previously presented for Gaussian processes. The approach is demonstrated on simulated and real-data examples.

Stochastic quasi-Newton with line-search regularization

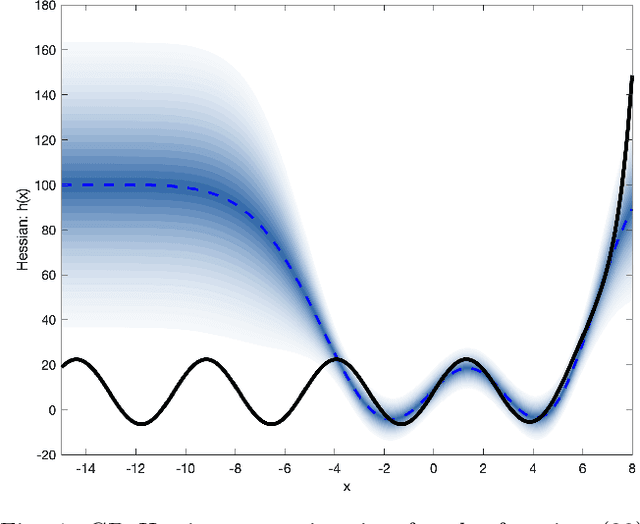
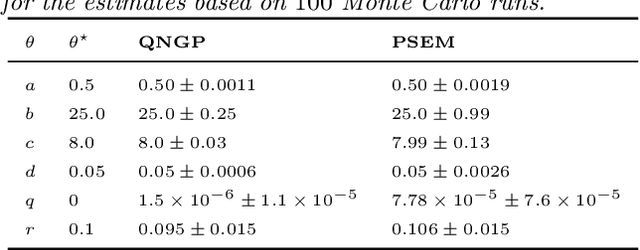
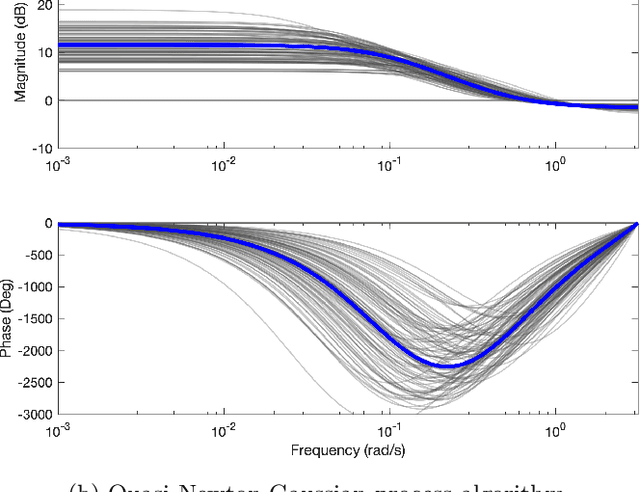
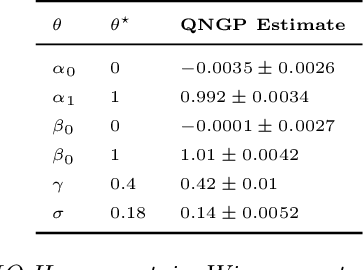
In this paper we present a novel quasi-Newton algorithm for use in stochastic optimisation. Quasi-Newton methods have had an enormous impact on deterministic optimisation problems because they afford rapid convergence and computationally attractive algorithms. In essence, this is achieved by learning the second-order (Hessian) information based on observing first-order gradients. We extend these ideas to the stochastic setting by employing a highly flexible model for the Hessian and infer its value based on observing noisy gradients. In addition, we propose a stochastic counterpart to standard line-search procedures and demonstrate the utility of this combination on maximum likelihood identification for general nonlinear state space models.

Inferring Heterogeneous Causal Effects in Presence of Spatial Confounding

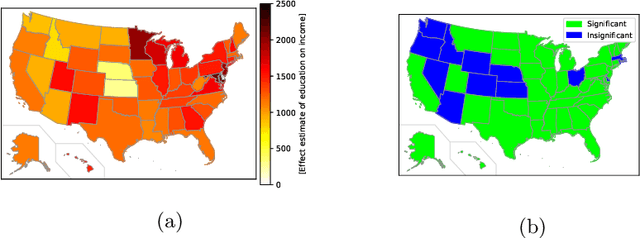
We address the problem of inferring the causal effect of an exposure on an outcome across space, using observational data. The data is possibly subject to unmeasured confounding variables which, in a standard approach, must be adjusted for by estimating a nuisance function. Here we develop a method that eliminates the nuisance function, while mitigating the resulting errors-in-variables. The result is a robust and accurate inference method for spatially varying heterogeneous causal effects. The properties of the method are demonstrated on synthetic as well as real data from Germany and the US.

Stochastic quasi-Newton with adaptive step lengths for large-scale problems

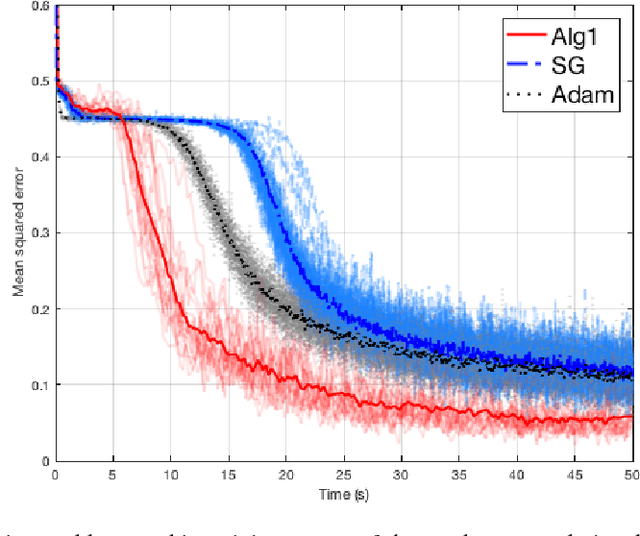
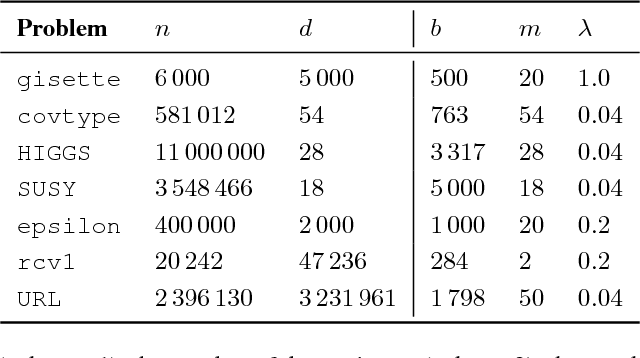
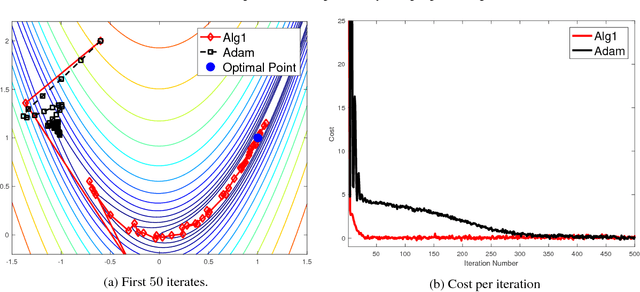
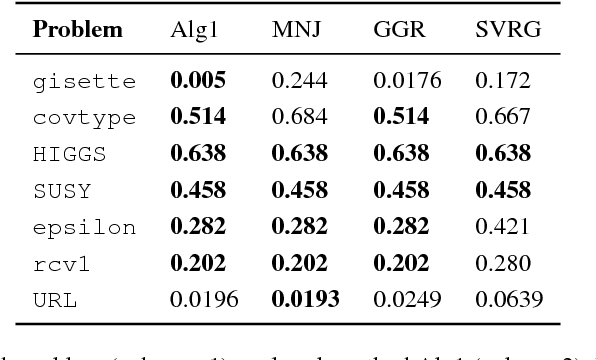
We provide a numerically robust and fast method capable of exploiting the local geometry when solving large-scale stochastic optimisation problems. Our key innovation is an auxiliary variable construction coupled with an inverse Hessian approximation computed using a receding history of iterates and gradients. It is the Markov chain nature of the classic stochastic gradient algorithm that enables this development. The construction offers a mechanism for stochastic line search adapting the step length. We numerically evaluate and compare against current state-of-the-art with encouraging performance on real-world benchmark problems where the number of observations and unknowns is in the order of millions.