Divide, Conquer, Combine Bayesian Decision Tree Sampling

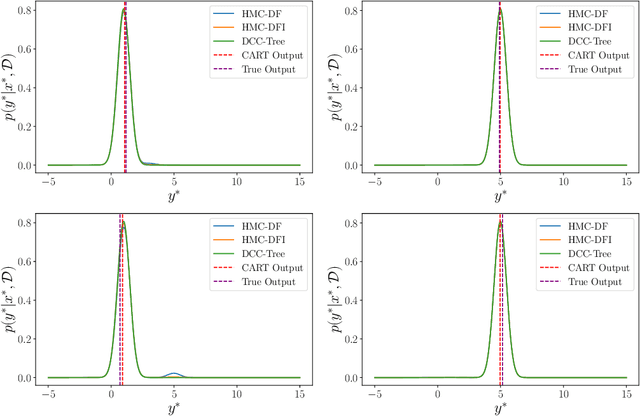
Decision trees are commonly used predictive models due to their flexibility and interpretability. This paper is directed at quantifying the uncertainty of decision tree predictions by employing a Bayesian inference approach. This is challenging because these approaches need to explore both the tree structure space and the space of decision parameters associated with each tree structure. This has been handled by using Markov Chain Monte Carlo (MCMC) methods, where a Markov Chain is constructed to provide samples from the desired Bayesian estimate. Importantly, the structure and the decision parameters are tightly coupled; small changes in the tree structure can demand vastly different decision parameters to provide accurate predictions. A challenge for existing MCMC approaches is proposing joint changes in both the tree structure and the decision parameters that result in efficient sampling. This paper takes a different approach, where each distinct tree structure is associated with a unique set of decision parameters. The proposed approach, entitled DCC-Tree, is inspired by the work in Zhou et al. [23] for probabilistic programs and Cochrane et al. [4] for Hamiltonian Monte Carlo (HMC) based sampling for decision trees. Results show that DCC-Tree performs comparably to other HMC-based methods and better than existing Bayesian tree methods while improving on consistency and reducing the per-proposal complexity.

A Probabilistically Motivated Learning Rate Adaptation for Stochastic Optimization

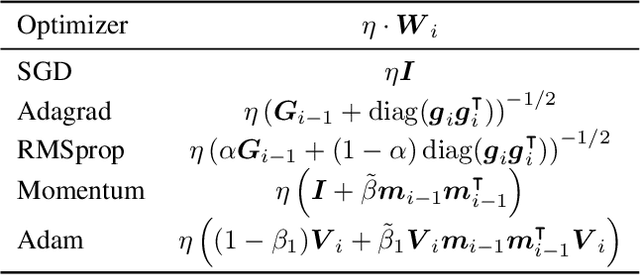
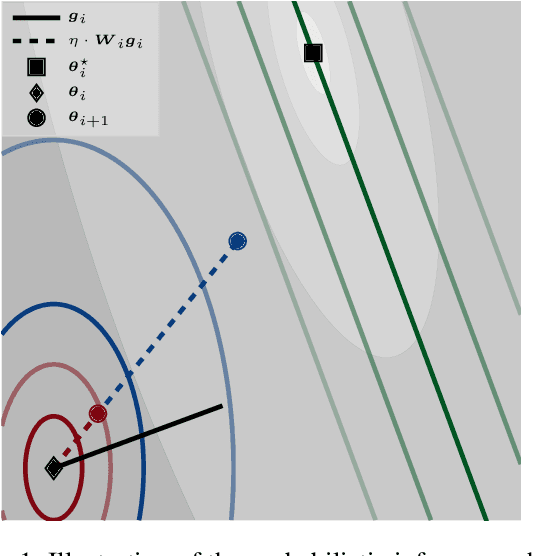
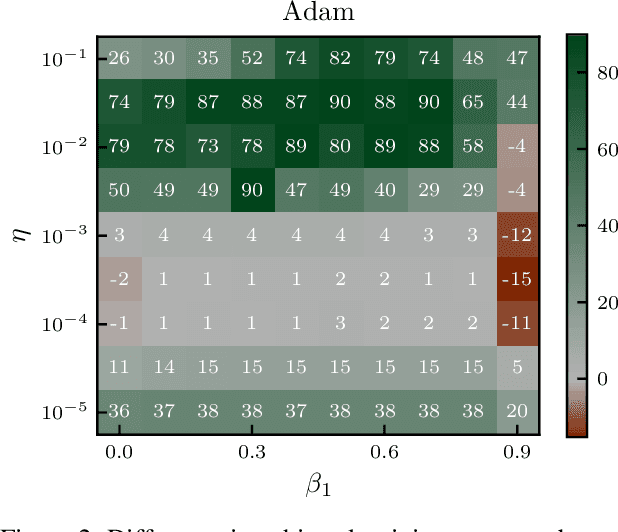
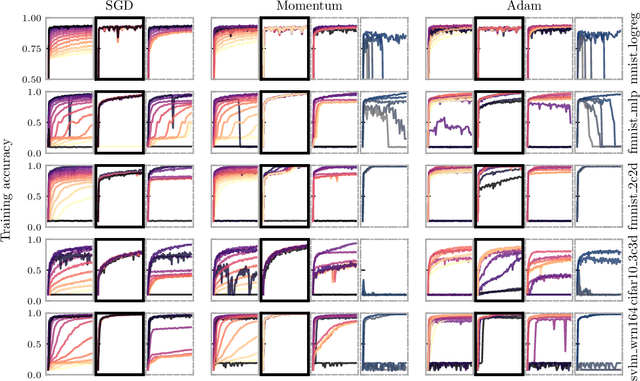
Machine learning practitioners invest significant manual and computational resources in finding suitable learning rates for optimization algorithms. We provide a probabilistic motivation, in terms of Gaussian inference, for popular stochastic first-order methods. As an important special case, it recovers the Polyak step with a general metric. The inference allows us to relate the learning rate to a dimensionless quantity that can be automatically adapted during training by a control algorithm. The resulting meta-algorithm is shown to adapt learning rates in a robust manner across a large range of initial values when applied to deep learning benchmark problems.

Variational State and Parameter Estimation

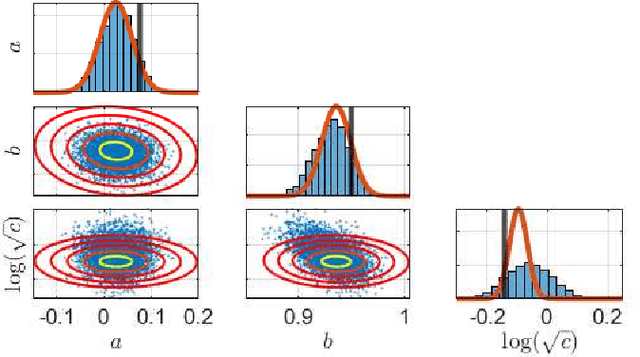
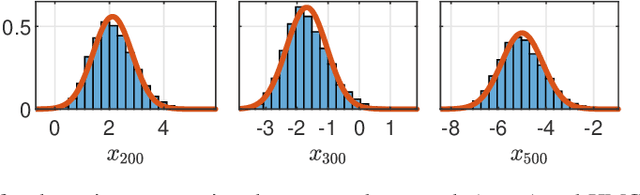
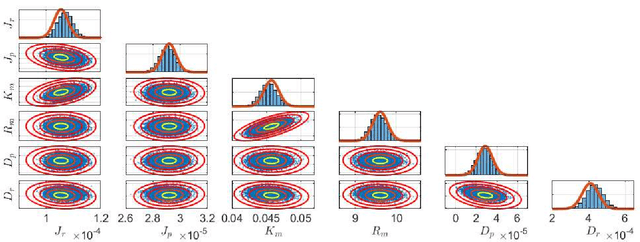
This paper considers the problem of computing Bayesian estimates of both states and model parameters for nonlinear state-space models. Generally, this problem does not have a tractable solution and approximations must be utilised. In this work, a variational approach is used to provide an assumed density which approximates the desired, intractable, distribution. The approach is deterministic and results in an optimisation problem of a standard form. Due to the parametrisation of the assumed density selected first- and second-order derivatives are readily available which allows for efficient solutions. The proposed method is compared against state-of-the-art Hamiltonian Monte Carlo in two numerical examples.

Variational Nonlinear System Identification

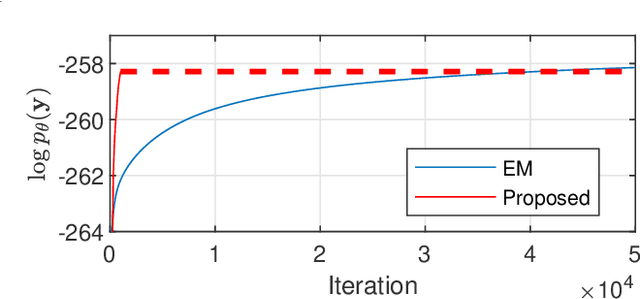
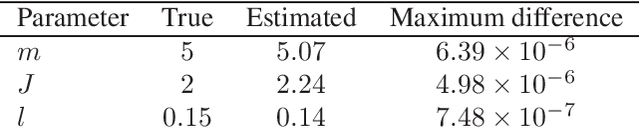
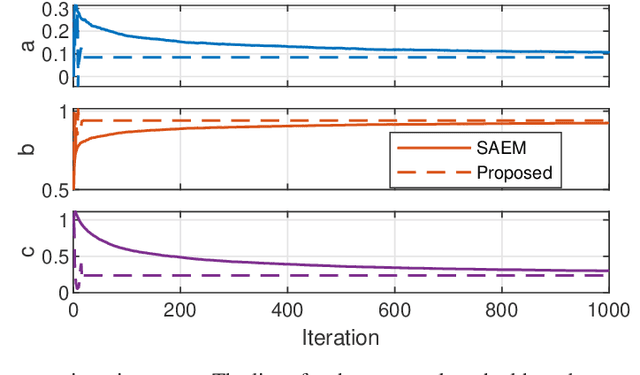
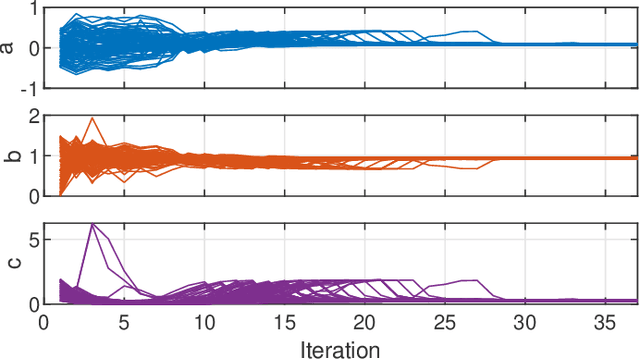
This paper considers parameter estimation for nonlinear state-space models, which is an important but challenging problem. We address this challenge by employing a variational inference (VI) approach, which is a principled method that has deep connections to maximum likelihood estimation. This VI approach ultimately provides estimates of the model as solutions to an optimisation problem, which is deterministic, tractable and can be solved using standard optimisation tools. A specialisation of this approach for systems with additive Gaussian noise is also detailed. The proposed method is examined numerically on a range of simulation and real examples with a focus on robustness to parameter initialisations; we additionally perform favourable comparisons against state-of-the-art alternatives.

A Heteroscedastic Likelihood Model for Two-frame Optical Flow

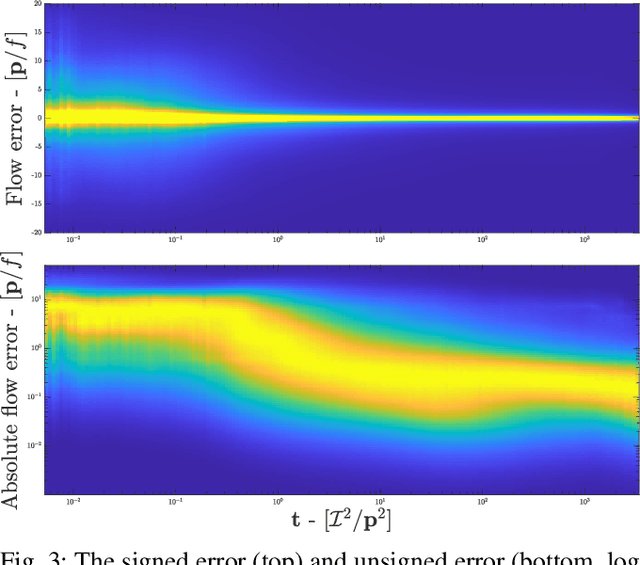
Machine vision is an important sensing technology used in mobile robotic systems. Advancing the autonomy of such systems requires accurate characterisation of sensor uncertainty. Vision includes intrinsic uncertainty due to the camera sensor and extrinsic uncertainty due to environmental lighting and texture, which propagate through the image processing algorithms used to produce visual measurements. To faithfully characterise visual measurements, we must take into account these uncertainties. In this paper, we propose a new class of likelihood functions that characterises the uncertainty of the error distribution of two-frame optical flow that enables a heteroscedastic dependence on texture. We employ the proposed class to characterise the Farneback and Lucas Kanade optical flow algorithms and achieve close agreement with their respective empirical error distributions over a wide range of texture in a simulated environment. The utility of the proposed likelihood model is demonstrated in a visual odometry ego-motion simulation study, which results in 30-83% reduction in position drift rate compared to traditional methods employing a Gaussian error assumption. The development of an empirically congruent likelihood model advances the requisite tool-set for vision-based Bayesian inference and enables sensor data fusion with GPS, LiDAR and IMU to advance robust autonomous navigation.

Constructing a variational family for nonlinear state-space models

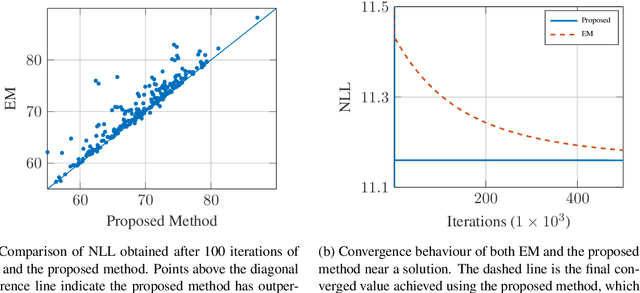
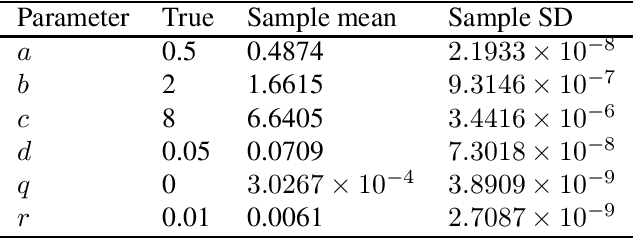
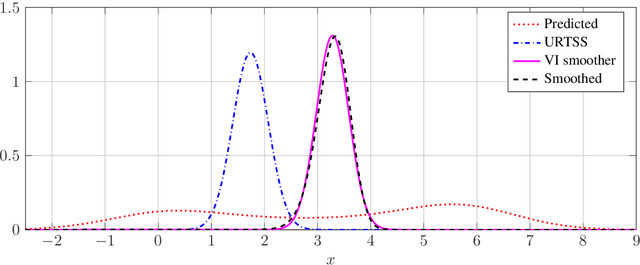
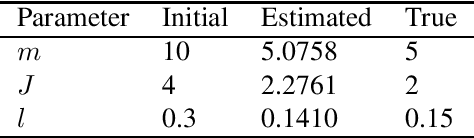
We consider the problem of maximum likelihood parameter estimation for nonlinear state-space models. This is an important, but challenging problem. This challenge stems from the intractable multidimensional integrals that must be solved in order to compute, and maximise, the likelihood. Here we present a new variational family where variational inference is used in combination with tractable approximations of these integrals resulting in a deterministic optimisation problem. Our developments also include a novel means for approximating the smoothed state distributions. We demonstrate our construction on several examples and show that they perform well compared to state of the art methods on real data-sets.

Linearly Constrained Neural Networks

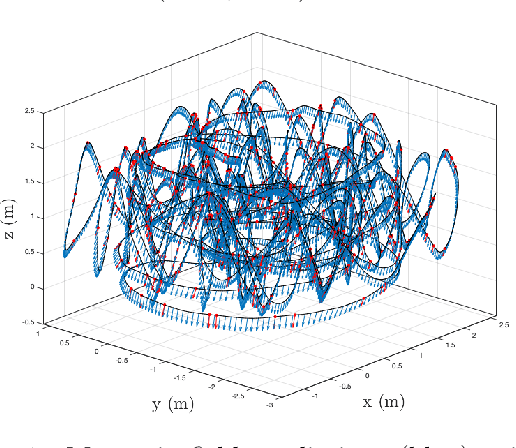
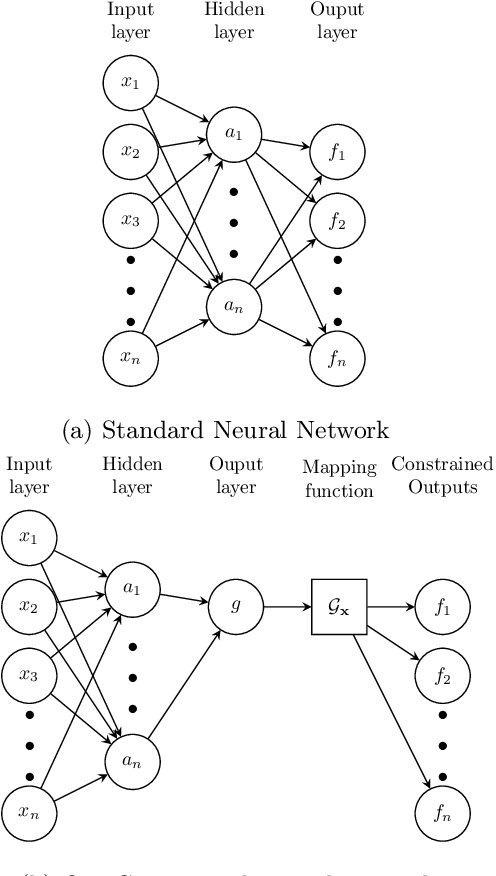
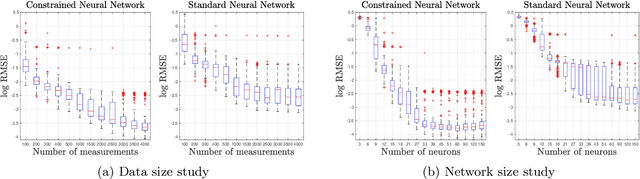
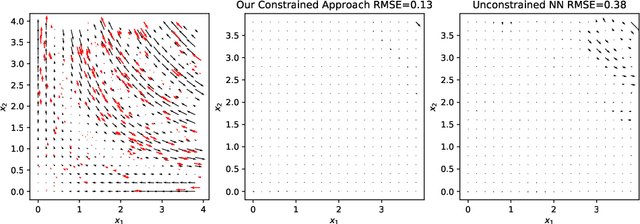
We present an approach to designing neural network based models that will explicitly satisfy known linear constraints. To achieve this, the target function is modelled as a linear transformation of an underlying function. This transformation is chosen such that any prediction of the target function is guaranteed to satisfy the constraints and can be determined from known physics or, more generally, by following a constructive procedure that was previously presented for Gaussian processes. The approach is demonstrated on simulated and real-data examples.

Learning Continuous Occupancy Maps with the Ising Process Model

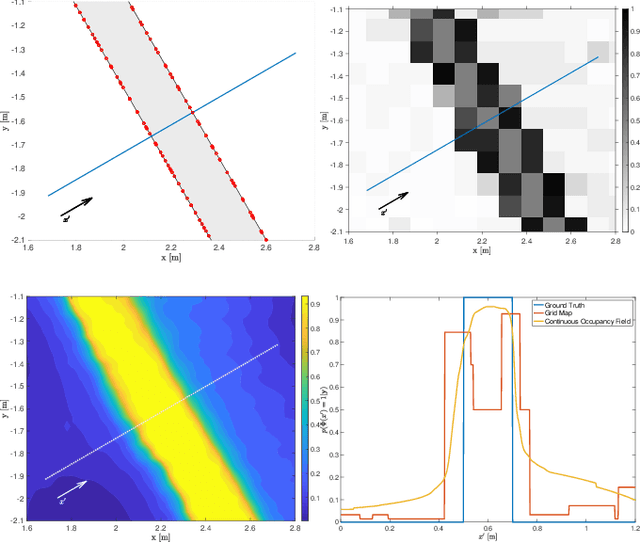
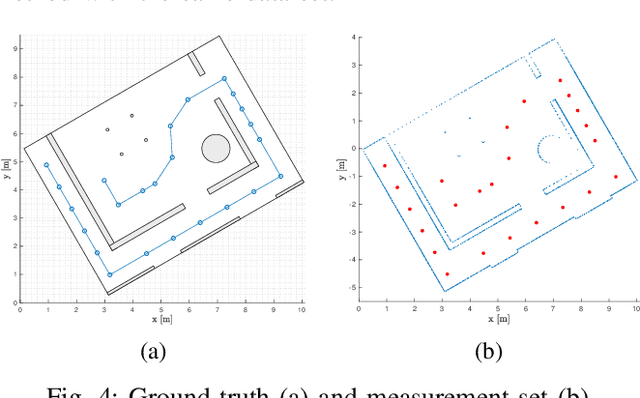
We present a new method of learning a continuous occupancy field for use in robot navigation. Occupancy grid maps, or variants of, are possibly the most widely used and accepted method of building a map of a robot's environment. Various methods have been developed to learn continuous occupancy maps and have successfully resolved many of the shortcomings of grid mapping, namely, priori discretisation and spatial correlation. However, most methods for producing a continuous occupancy field remain computationally expensive or heuristic in nature. Our method explores a generalisation of the so-called Ising model as a suitable candidate for modelling an occupancy field. We also present a unique kernel for use within our method that models range measurements. The method is quite attractive as it requires only a small number of hyperparameters to be trained, and is computationally efficient. The small number of hyperparameters can be quickly learned by maximising a pseudo likelihood. The technique is demonstrated on both a small simulated indoor environment with known ground truth as well as large indoor and outdoor areas, using two common real data sets.

Deep kernel learning for integral measurements

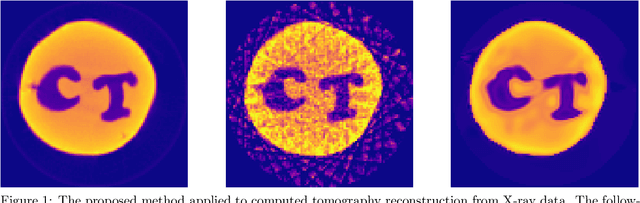
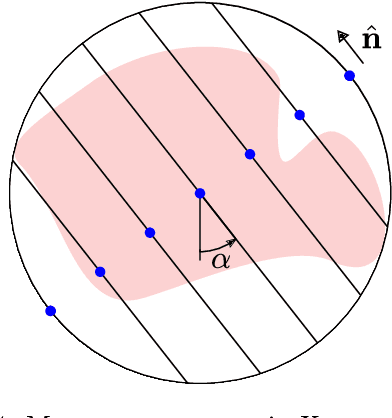
Deep kernel learning refers to a Gaussian process that incorporates neural networks to improve the modelling of complex functions. We present a method that makes this approach feasible for problems where the data consists of line integral measurements of the target function. The performance is illustrated on computed tomography reconstruction examples.

Stochastic quasi-Newton with line-search regularization

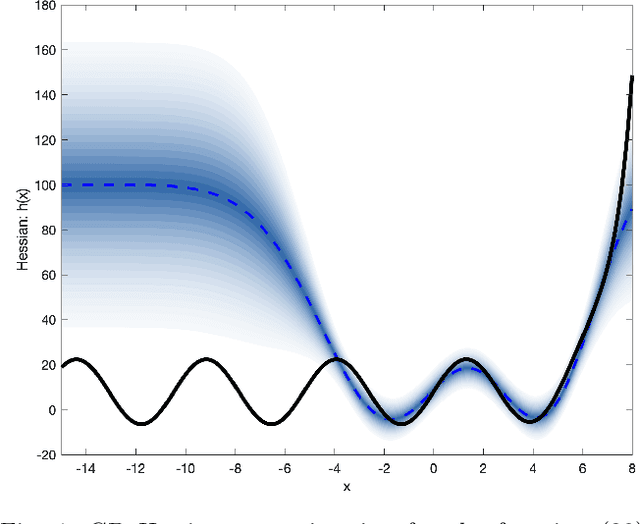
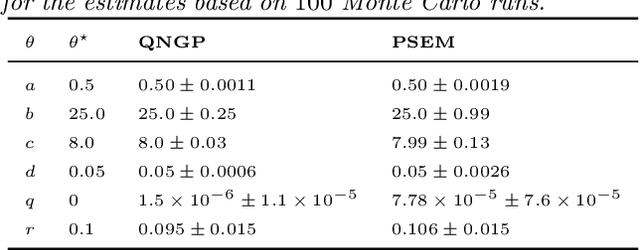
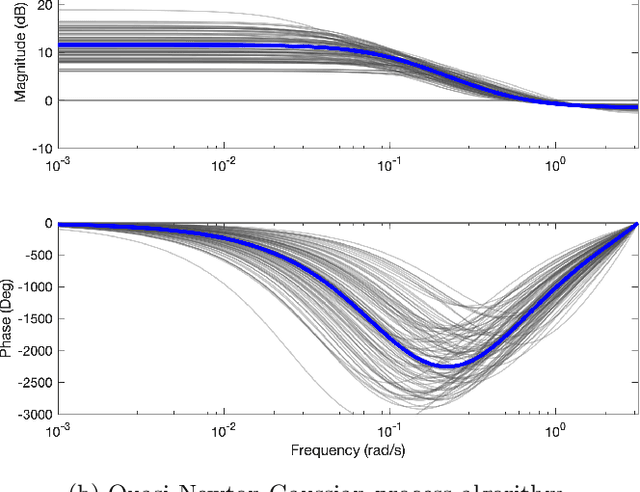
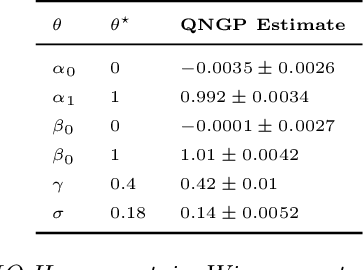
In this paper we present a novel quasi-Newton algorithm for use in stochastic optimisation. Quasi-Newton methods have had an enormous impact on deterministic optimisation problems because they afford rapid convergence and computationally attractive algorithms. In essence, this is achieved by learning the second-order (Hessian) information based on observing first-order gradients. We extend these ideas to the stochastic setting by employing a highly flexible model for the Hessian and infer its value based on observing noisy gradients. In addition, we propose a stochastic counterpart to standard line-search procedures and demonstrate the utility of this combination on maximum likelihood identification for general nonlinear state space models.