A Probabilistically Motivated Learning Rate Adaptation for Stochastic Optimization

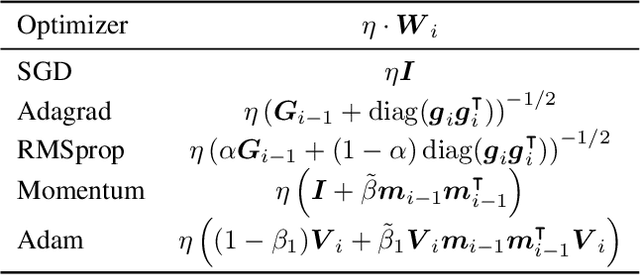
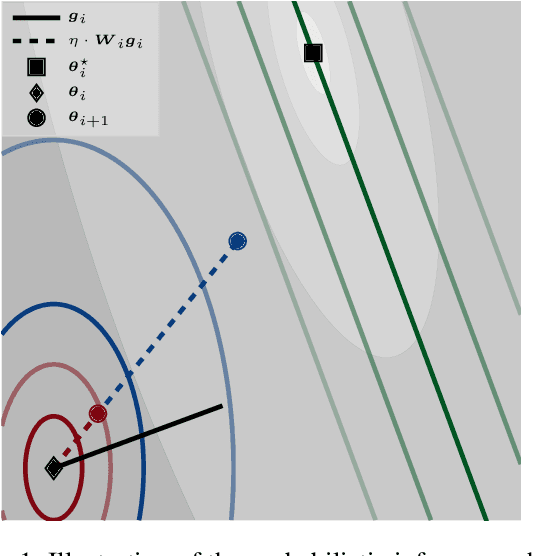
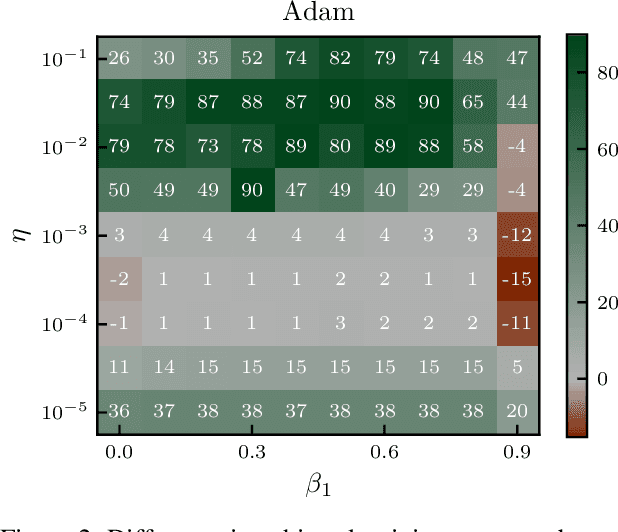
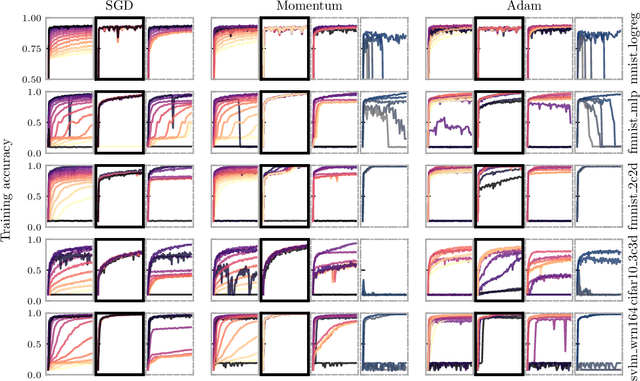
Machine learning practitioners invest significant manual and computational resources in finding suitable learning rates for optimization algorithms. We provide a probabilistic motivation, in terms of Gaussian inference, for popular stochastic first-order methods. As an important special case, it recovers the Polyak step with a general metric. The inference allows us to relate the learning rate to a dimensionless quantity that can be automatically adapted during training by a control algorithm. The resulting meta-algorithm is shown to adapt learning rates in a robust manner across a large range of initial values when applied to deep learning benchmark problems.

High-Dimensional Gaussian Process Inference with Derivatives

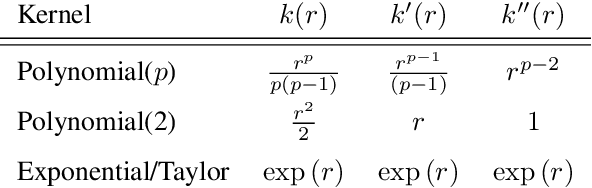
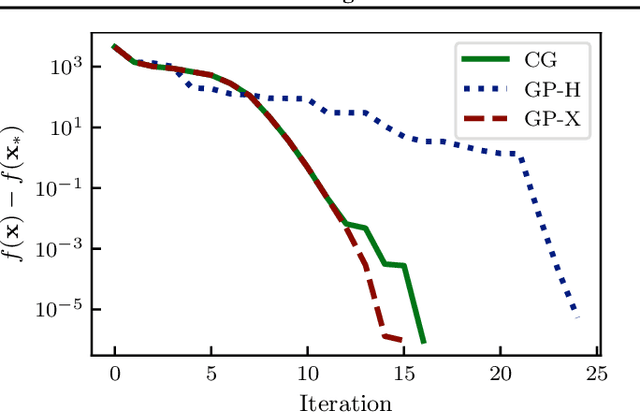
Although it is widely known that Gaussian processes can be conditioned on observations of the gradient, this functionality is of limited use due to the prohibitive computational cost of $\mathcal{O}(N^3 D^3)$ in data points $N$ and dimension $D$. The dilemma of gradient observations is that a single one of them comes at the same cost as $D$ independent function evaluations, so the latter are often preferred. Careful scrutiny reveals, however, that derivative observations give rise to highly structured kernel Gram matrices for very general classes of kernels (inter alia, stationary kernels). We show that in the low-data regime $N<D$, the Gram matrix can be decomposed in a manner that reduces the cost of inference to $\mathcal{O}(N^2D + (N^2)^3)$ (i.e., linear in the number of dimensions) and, in special cases, to $\mathcal{O}(N^2D + N^3)$. This reduction in complexity opens up new use-cases for inference with gradients especially in the high-dimensional regime, where the information-to-cost ratio of gradient observations significantly increases. We demonstrate this potential in a variety of tasks relevant for machine learning, such as optimization and Hamiltonian Monte Carlo with predictive gradients.

Active Probabilistic Inference on Matrices for Pre-Conditioning in Stochastic Optimization

Pre-conditioning is a well-known concept that can significantly improve the convergence of optimization algorithms. For noise-free problems, where good pre-conditioners are not known a priori, iterative linear algebra methods offer one way to efficiently construct them. For the stochastic optimization problems that dominate contemporary machine learning, however, this approach is not readily available. We propose an iterative algorithm inspired by classic iterative linear solvers that uses a probabilistic model to actively infer a pre-conditioner in situations where Hessian-projections can only be constructed with strong Gaussian noise. The algorithm is empirically demonstrated to efficiently construct effective pre-conditioners for stochastic gradient descent and its variants. Experiments on problems of comparably low dimensionality show improved convergence. In very high-dimensional problems, such as those encountered in deep learning, the pre-conditioner effectively becomes an automatic learning-rate adaptation scheme, which we also empirically show to work well.

Krylov Subspace Recycling for Fast Iterative Least-Squares in Machine Learning

Solving symmetric positive definite linear problems is a fundamental computational task in machine learning. The exact solution, famously, is cubicly expensive in the size of the matrix. To alleviate this problem, several linear-time approximations, such as spectral and inducing-point methods, have been suggested and are now in wide use. These are low-rank approximations that choose the low-rank space a priori and do not refine it over time. While this allows linear cost in the data-set size, it also causes a finite, uncorrected approximation error. Authors from numerical linear algebra have explored ways to iteratively refine such low-rank approximations, at a cost of a small number of matrix-vector multiplications. This idea is particularly interesting in the many situations in machine learning where one has to solve a sequence of related symmetric positive definite linear problems. From the machine learning perspective, such deflation methods can be interpreted as transfer learning of a low-rank approximation across a time-series of numerical tasks. We study the use of such methods for our field. Our empirical results show that, on regression and classification problems of intermediate size, this approach can interpolate between low computational cost and numerical precision.