Incorporating Sum Constraints into Multitask Gaussian Processes

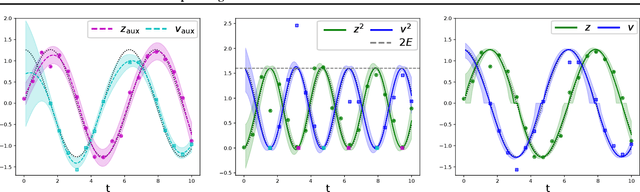
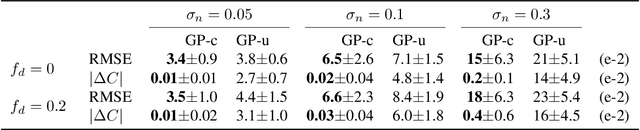
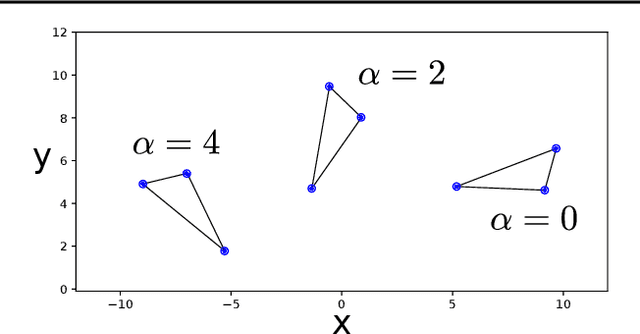
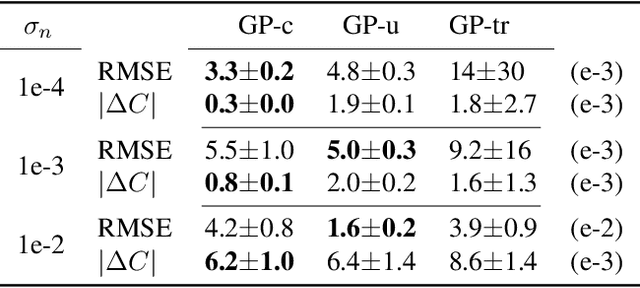
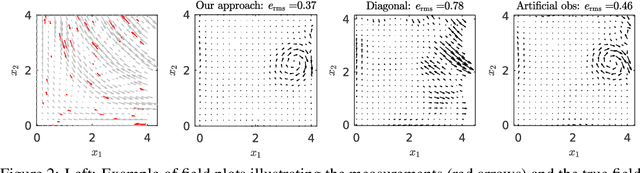
Machine learning models can be improved by adapting them to respect existing background knowledge. In this paper we consider multitask Gaussian processes, with background knowledge in the form of constraints that require a specific sum of the outputs to be constant. This is achieved by conditioning the prior distribution on the constraint fulfillment. The approach allows for both linear and nonlinear constraints. We demonstrate that the constraints are fulfilled with high precision and that the construction can improve the overall prediction accuracy as compared to the standard Gaussian process.

A Probabilistically Motivated Learning Rate Adaptation for Stochastic Optimization

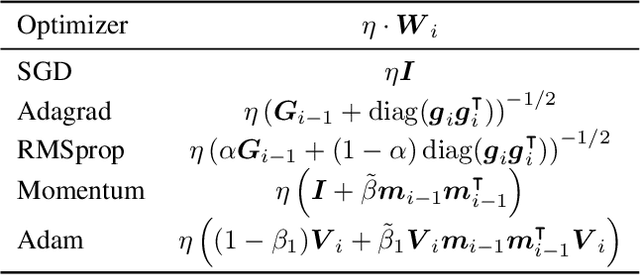
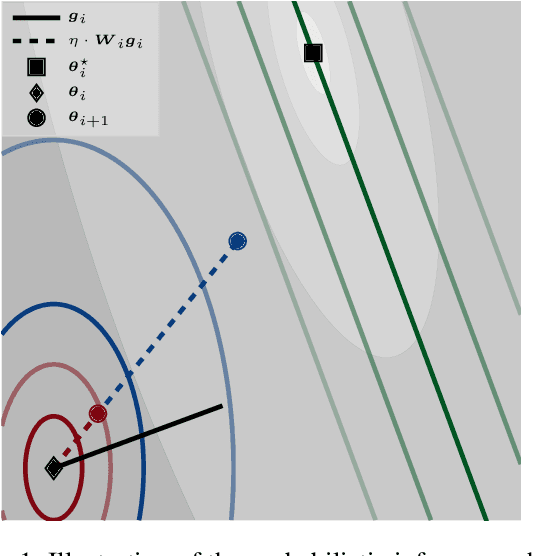
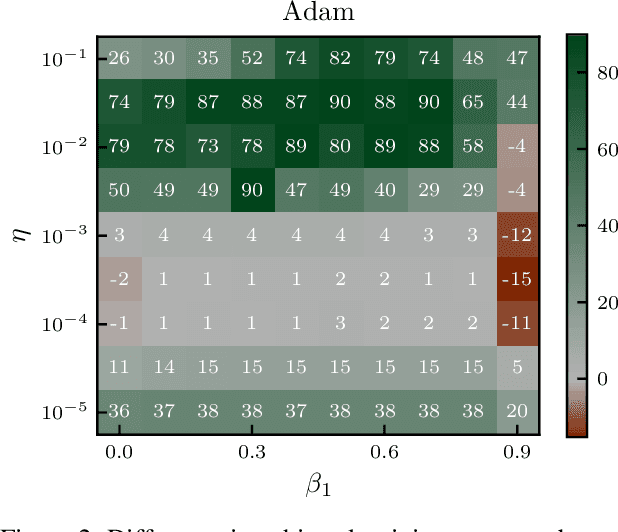
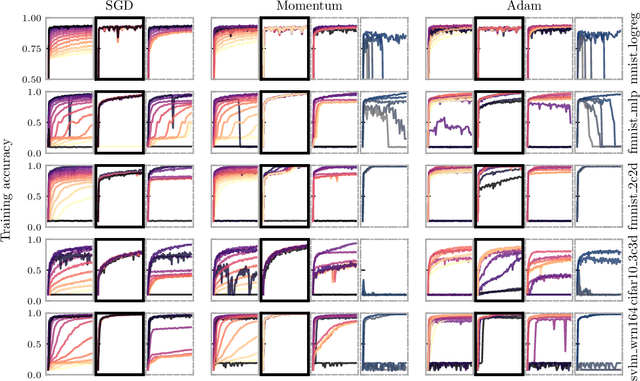
Machine learning practitioners invest significant manual and computational resources in finding suitable learning rates for optimization algorithms. We provide a probabilistic motivation, in terms of Gaussian inference, for popular stochastic first-order methods. As an important special case, it recovers the Polyak step with a general metric. The inference allows us to relate the learning rate to a dimensionless quantity that can be automatically adapted during training by a control algorithm. The resulting meta-algorithm is shown to adapt learning rates in a robust manner across a large range of initial values when applied to deep learning benchmark problems.

Linearly Constrained Neural Networks

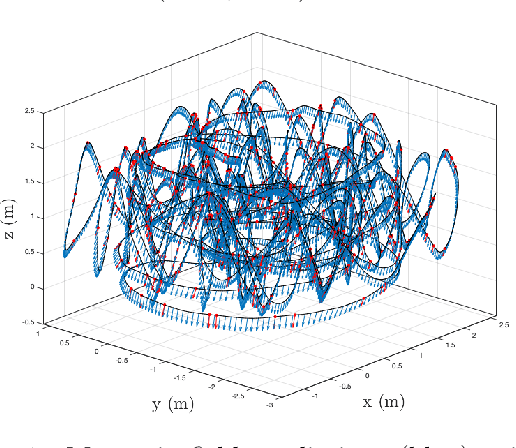
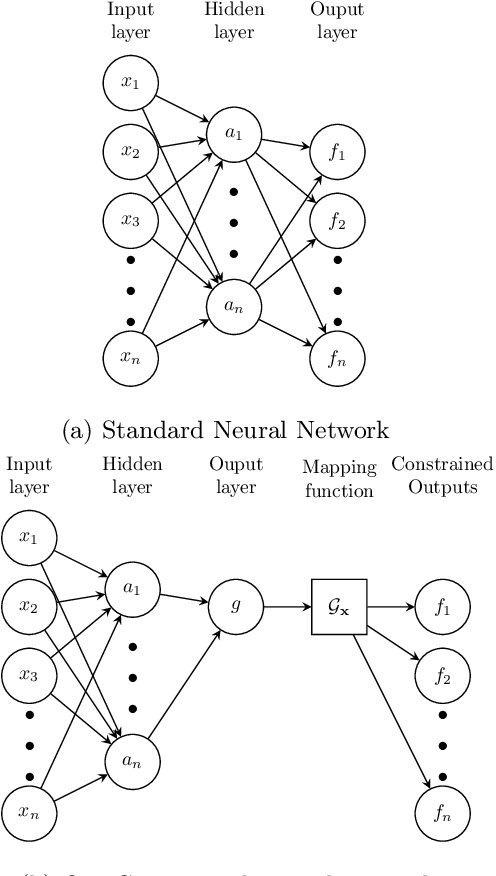
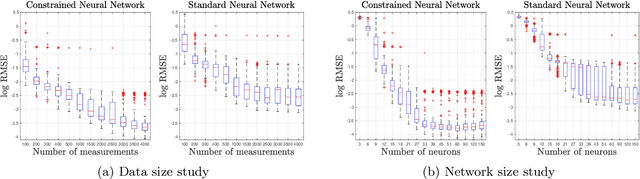
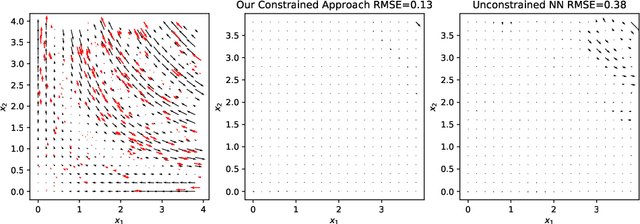
We present an approach to designing neural network based models that will explicitly satisfy known linear constraints. To achieve this, the target function is modelled as a linear transformation of an underlying function. This transformation is chosen such that any prediction of the target function is guaranteed to satisfy the constraints and can be determined from known physics or, more generally, by following a constructive procedure that was previously presented for Gaussian processes. The approach is demonstrated on simulated and real-data examples.

Deep kernel learning for integral measurements

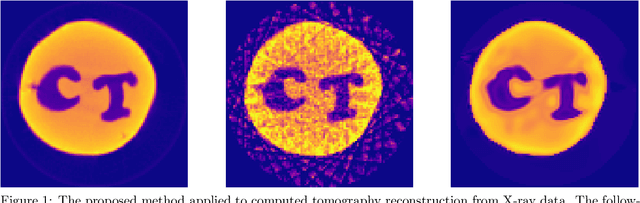
Deep kernel learning refers to a Gaussian process that incorporates neural networks to improve the modelling of complex functions. We present a method that makes this approach feasible for problems where the data consists of line integral measurements of the target function. The performance is illustrated on computed tomography reconstruction examples.

A fast quasi-Newton-type method for large-scale stochastic optimisation

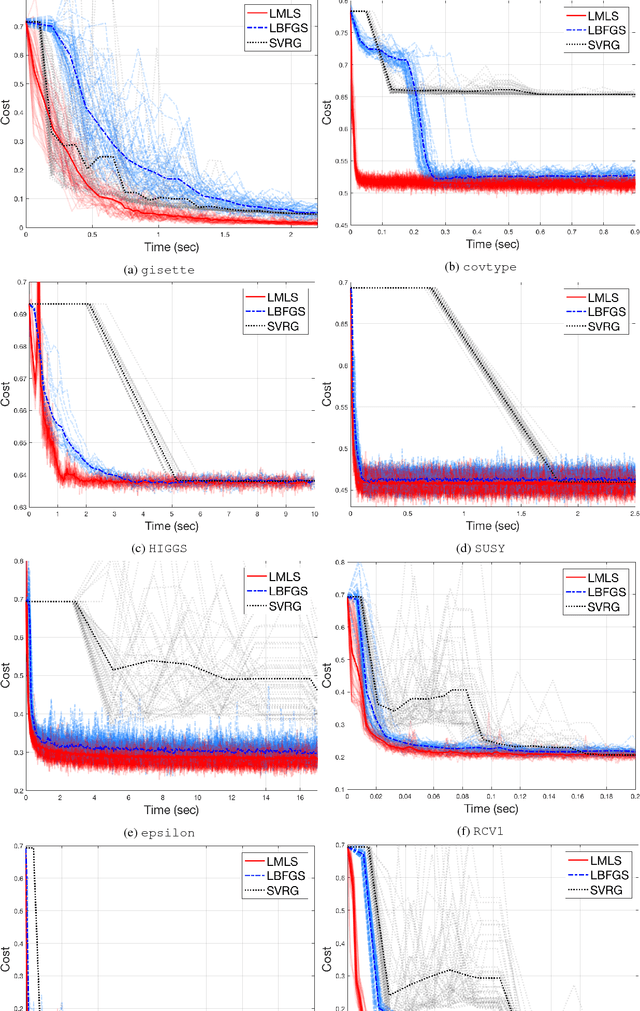
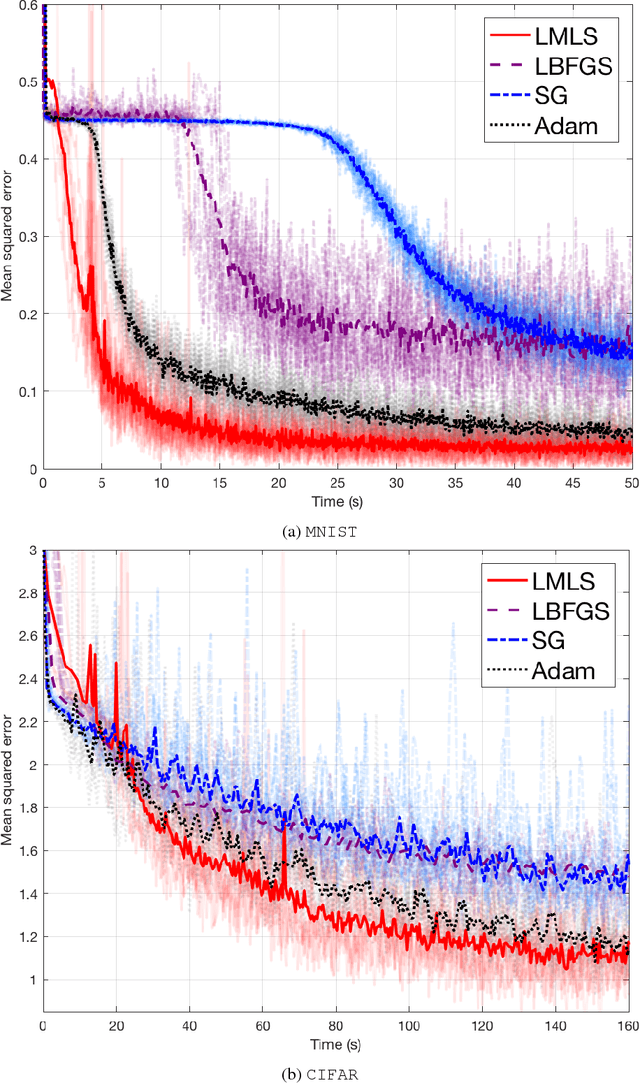
During recent years there has been an increased interest in stochastic adaptations of limited memory quasi-Newton methods, which compared to pure gradient-based routines can improve the convergence by incorporating second order information. In this work we propose a direct least-squares approach conceptually similar to the limited memory quasi-Newton methods, but that computes the search direction in a slightly different way. This is achieved in a fast and numerically robust manner by maintaining a Cholesky factor of low dimension. This is combined with a stochastic line search relying upon fulfilment of the Wolfe condition in a backtracking manner, where the step length is adaptively modified with respect to the optimisation progress. We support our new algorithm by providing several theoretical results guaranteeing its performance. The performance is demonstrated on real-world benchmark problems which shows improved results in comparison with already established methods.

Probabilistic approach to limited-data computed tomography reconstruction

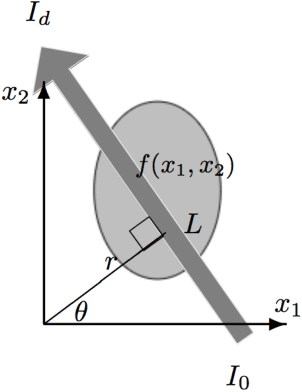
We consider the problem of reconstructing the internal structure of an object from limited x-ray projections. In this work, we use a Gaussian process to model the target function. In contrast to other established methods, this comes with the advantage of not requiring any manual parameter tuning, which usually arises in classical regularization strategies. The Gaussian process is well-known in a heavy computation for the inversion of a covariance matrix, and in this work, by employing an approximative spectral-based technique, we reduce the computational complexity and avoid the need of numerical integration. Results from simulated and real data indicate that this approach is less sensitive to streak artifacts as compared to the commonly used method of filteredback projection, an analytic reconstruction algorithm using Radon inversion formula.

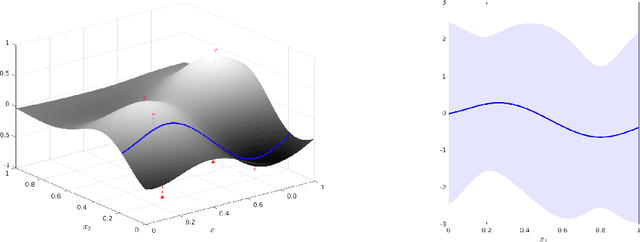
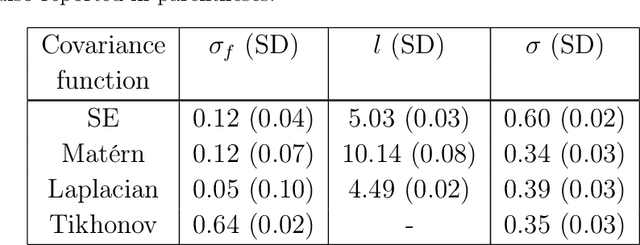
Linearly constrained Gaussian processes

We consider a modification of the covariance function in Gaussian processes to correctly account for known linear constraints. By modelling the target function as a transformation of an underlying function, the constraints are explicitly incorporated in the model such that they are guaranteed to be fulfilled by any sample drawn or prediction made. We also propose a constructive procedure for designing the transformation operator and illustrate the result on both simulated and real-data examples.