Niklas Wahlström
Learning Dynamics from Input-Output Data with Hamiltonian Gaussian Processes
Nov 07, 2025Abstract:Embedding non-restrictive prior knowledge, such as energy conservation laws, in learning-based approaches is a key motive to construct physically consistent models from limited data, relevant for, e.g., model-based control. Recent work incorporates Hamiltonian dynamics into Gaussian Process (GP) regression to obtain uncertainty-quantifying models that adhere to the underlying physical principles. However, these works rely on velocity or momentum data, which is rarely available in practice. In this paper, we consider dynamics learning with non-conservative Hamiltonian GPs, and address the more realistic problem setting of learning from input-output data. We provide a fully Bayesian scheme for estimating probability densities of unknown hidden states, of GP hyperparameters, as well as of structural hyperparameters, such as damping coefficients. Considering the computational complexity of GPs, we take advantage of a reduced-rank GP approximation and leverage its properties for computationally efficient prediction and training. The proposed method is evaluated in a nonlinear simulation case study and compared to a state-of-the-art approach that relies on momentum measurements.
Repulsive Ensembles for Bayesian Inference in Physics-informed Neural Networks
May 22, 2025Abstract:Physics-informed neural networks (PINNs) have proven an effective tool for solving differential equations, in particular when considering non-standard or ill-posed settings. When inferring solutions and parameters of the differential equation from data, uncertainty estimates are preferable to point estimates, as they give an idea about the accuracy of the solution. In this work, we consider the inverse problem and employ repulsive ensembles of PINNs (RE-PINN) for obtaining such estimates. The repulsion is implemented by adding a particular repulsive term to the loss function, which has the property that the ensemble predictions correspond to the true Bayesian posterior in the limit of infinite ensemble members. Where possible, we compare the ensemble predictions to Monte Carlo baselines. Whereas the standard ensemble tends to collapse to maximum-a-posteriori solutions, the repulsive ensemble produces significantly more accurate uncertainty estimates and exhibits higher sample diversity.
Probabilistic matching of real and generated data statistics in generative adversarial networks
Jun 19, 2023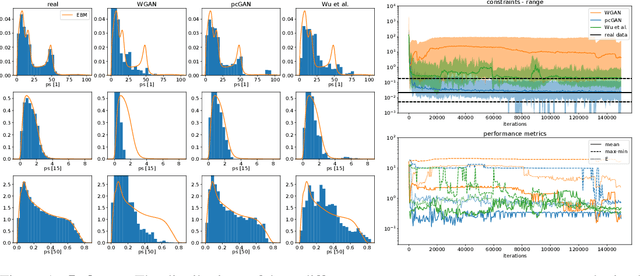
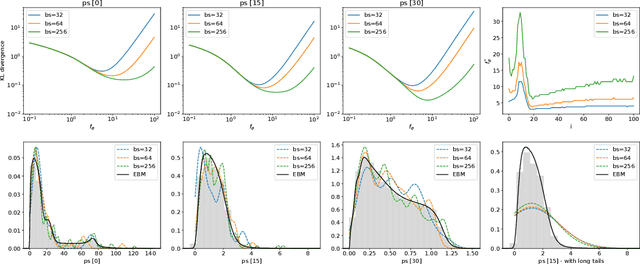

Abstract:Generative adversarial networks constitute a powerful approach to generative modeling. While generated samples often are indistinguishable from real data, there is no guarantee that they will follow the true data distribution. In this work, we propose a method to ensure that the distributions of certain generated data statistics coincide with the respective distributions of the real data. In order to achieve this, we add a Kullback-Leibler term to the generator loss function: the KL divergence is taken between the true distributions as represented by a conditional energy-based model, and the corresponding generated distributions obtained from minibatch values at each iteration. We evaluate the method on a synthetic dataset and two real-world datasets and demonstrate improved performance of our method.
Invertible Kernel PCA with Random Fourier Features
Mar 09, 2023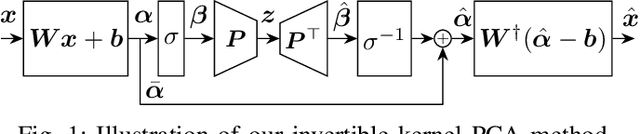
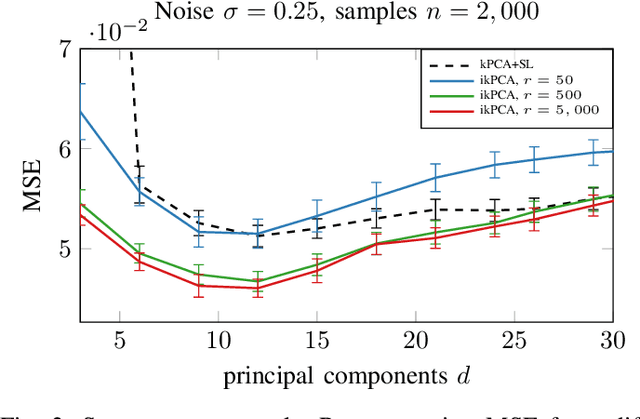
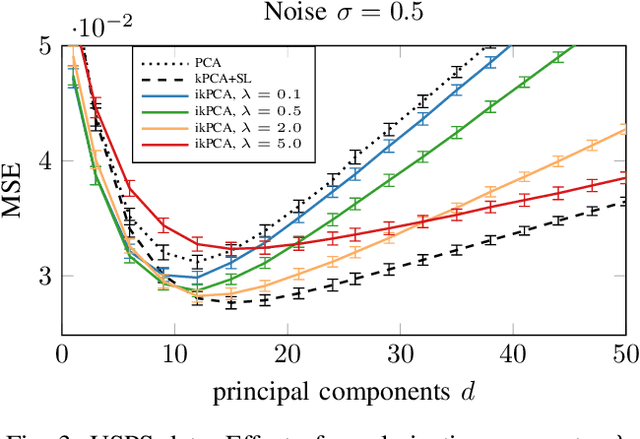
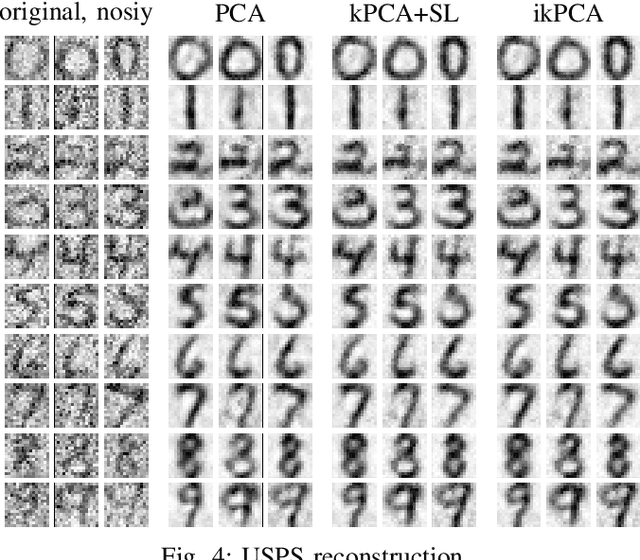
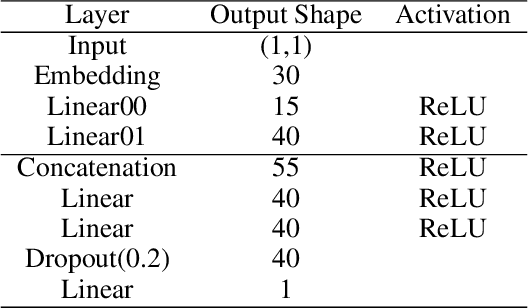
Abstract:Kernel principal component analysis (kPCA) is a widely studied method to construct a low-dimensional data representation after a nonlinear transformation. The prevailing method to reconstruct the original input signal from kPCA -- an important task for denoising -- requires us to solve a supervised learning problem. In this paper, we present an alternative method where the reconstruction follows naturally from the compression step. We first approximate the kernel with random Fourier features. Then, we exploit the fact that the nonlinear transformation is invertible in a certain subdomain. Hence, the name \emph{invertible kernel PCA (ikPCA)}. We experiment with different data modalities and show that ikPCA performs similarly to kPCA with supervised reconstruction on denoising tasks, making it a strong alternative.
Physics-informed neural networks with unknown measurement noise
Nov 28, 2022Abstract:Physics-informed neural networks (PINNs) constitute a flexible approach to both finding solutions and identifying parameters of partial differential equations. Most works on the topic assume noiseless data, or data contaminated by weak Gaussian noise. We show that the standard PINN framework breaks down in case of non-Gaussian noise. We give a way of resolving this fundamental issue and we propose to jointly train an energy-based model (EBM) to learn the correct noise distribution. We illustrate the improved performance of our approach using multiple examples.
Incorporating Sum Constraints into Multitask Gaussian Processes
Feb 03, 2022
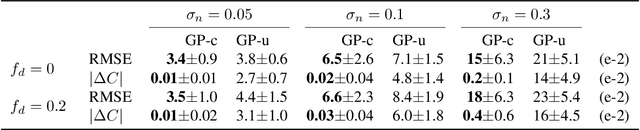
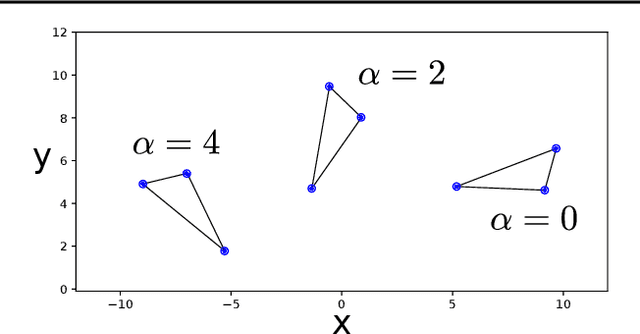
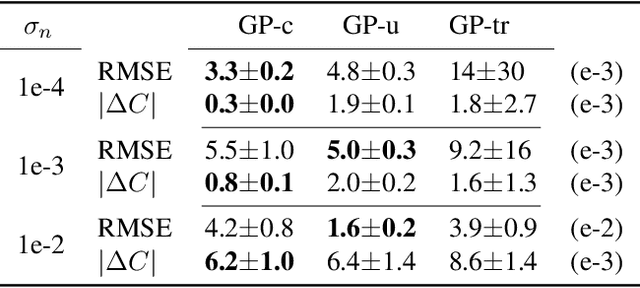
Abstract:Machine learning models can be improved by adapting them to respect existing background knowledge. In this paper we consider multitask Gaussian processes, with background knowledge in the form of constraints that require a specific sum of the outputs to be constant. This is achieved by conditioning the prior distribution on the constraint fulfillment. The approach allows for both linear and nonlinear constraints. We demonstrate that the constraints are fulfilled with high precision and that the construction can improve the overall prediction accuracy as compared to the standard Gaussian process.
Learning deep autoregressive models for hierarchical data
May 06, 2021
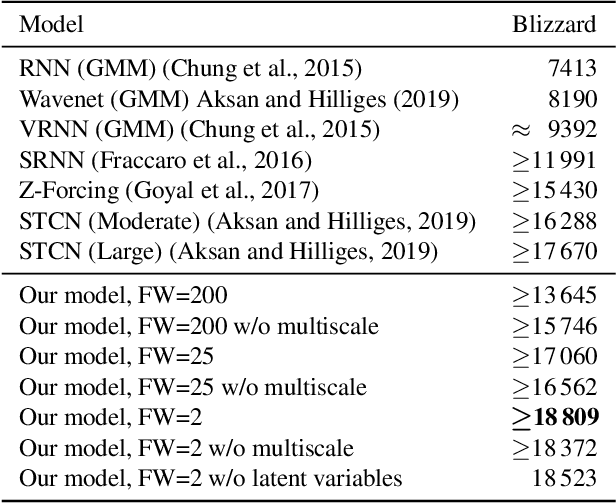
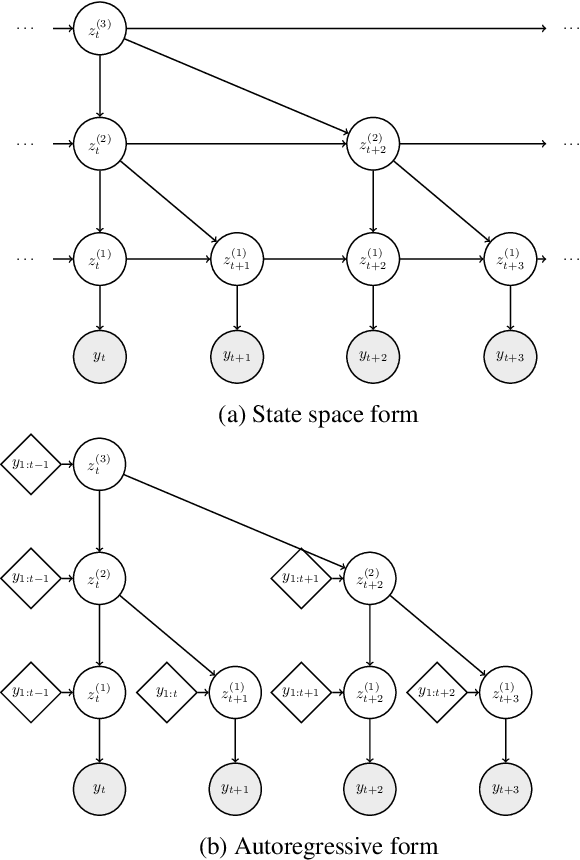
Abstract:We propose a model for hierarchical structured data as an extension to the stochastic temporal convolutional network. The proposed model combines an autoregressive model with a hierarchical variational autoencoder and downsampling to achieve superior computational complexity. We evaluate the proposed model on two different types of sequential data: speech and handwritten text. The results are promising with the proposed model achieving state-of-the-art performance.
Deep State Space Models for Nonlinear System Identification
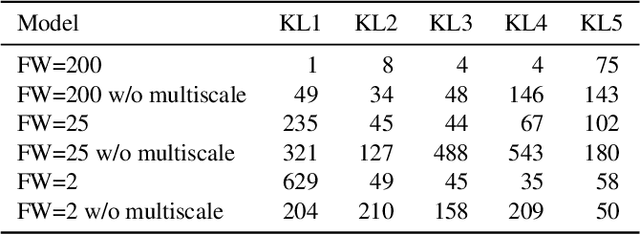
Mar 31, 2020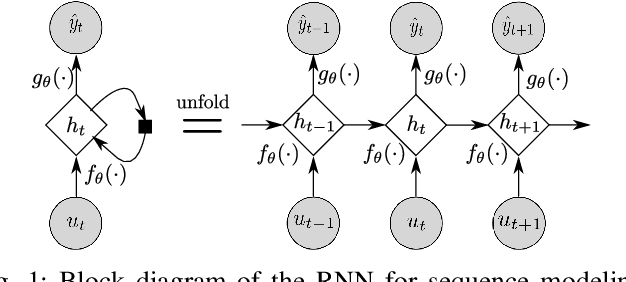
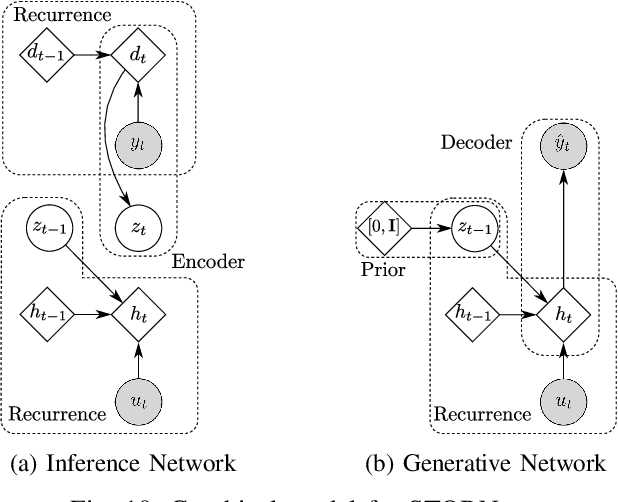
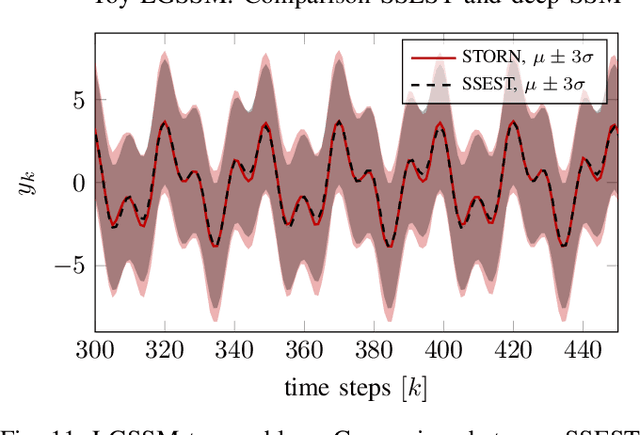
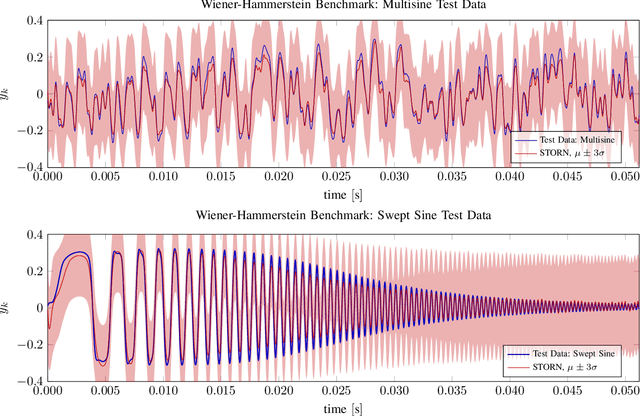
Abstract:An actively evolving model class for generative temporal models developed in the deep learning community are deep state space models (SSMs) which have a close connection to classic SSMs. In this work six new deep SSMs are implemented and evaluated for the identification of established nonlinear dynamic system benchmarks. The models and their parameter learning algorithms are elaborated rigorously. The usage of deep SSMs as a black-box identification model can describe a wide range of dynamics due to the flexibility of deep neural networks. Additionally, the uncertainty of the system is modelled and therefore one obtains a much richer representation and a whole class of systems to describe the underlying dynamics.
Deep Convolutional Networks in System Identification
Sep 04, 2019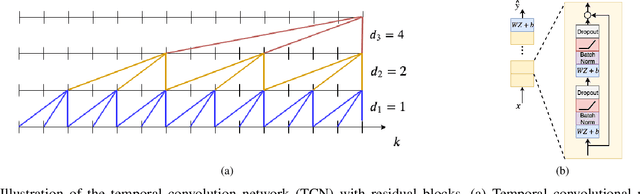
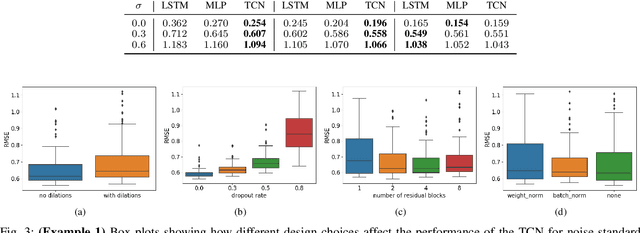
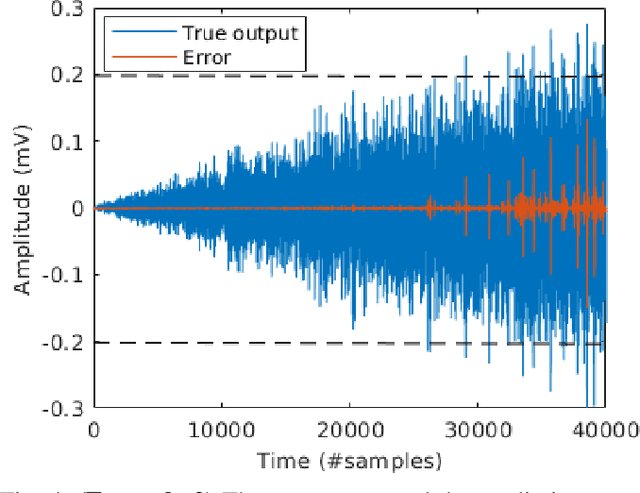
Abstract:Recent developments within deep learning are relevant for nonlinear system identification problems. In this paper, we establish connections between the deep learning and the system identification communities. It has recently been shown that convolutional architectures are at least as capable as recurrent architectures when it comes to sequence modeling tasks. Inspired by these results we explore the explicit relationships between the recently proposed temporal convolutional network (TCN) and two classic system identification model structures; Volterra series and block-oriented models. We end the paper with an experimental study where we provide results on two real-world problems, the well-known Silverbox dataset and a newer dataset originating from ground vibration experiments on an F-16 fighter aircraft.
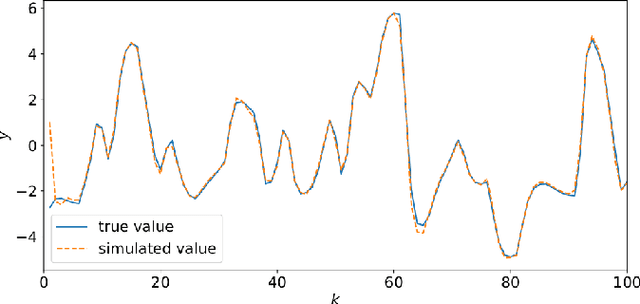
Data-Driven Impulse Response Regularization via Deep Learning
Oct 11, 2018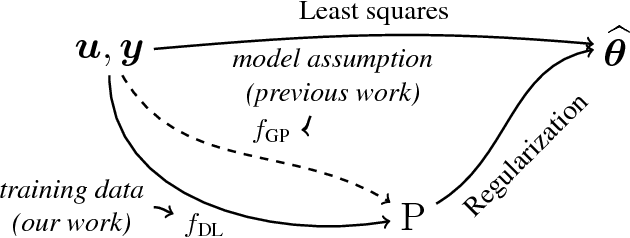
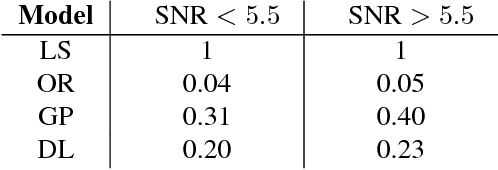
Abstract:We consider the problem of impulse response estimation of stable linear single-input single-output systems. It is a well-studied problem where flexible non-parametric models recently offered a leap in performance compared to the classical finite-dimensional model structures. Inspired by this development and the success of deep learning we propose a new flexible data-driven model. Our experiments indicate that the new model is capable of exploiting even more of the hidden patterns that are present in the input-output data as compared to the non-parametric models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge