Probabilistic approach to limited-data computed tomography reconstruction
Paper and Code
Sep 11, 2018

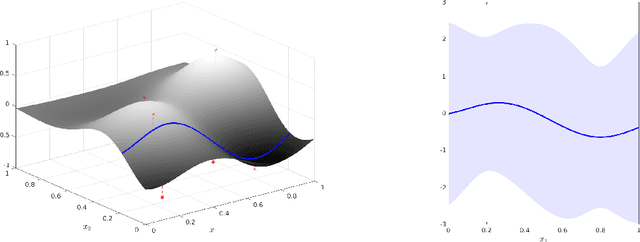
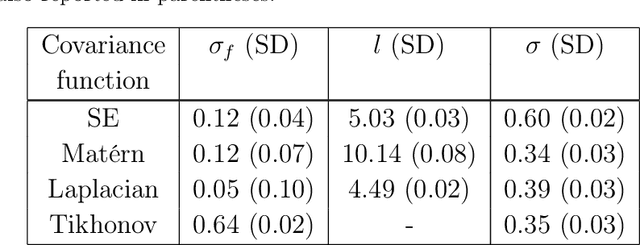
We consider the problem of reconstructing the internal structure of an object from limited x-ray projections. In this work, we use a Gaussian process to model the target function. In contrast to other established methods, this comes with the advantage of not requiring any manual parameter tuning, which usually arises in classical regularization strategies. The Gaussian process is well-known in a heavy computation for the inversion of a covariance matrix, and in this work, by employing an approximative spectral-based technique, we reduce the computational complexity and avoid the need of numerical integration. Results from simulated and real data indicate that this approach is less sensitive to streak artifacts as compared to the commonly used method of filteredback projection, an analytic reconstruction algorithm using Radon inversion formula.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge