Repulsive Ensembles for Bayesian Inference in Physics-informed Neural Networks

Physics-informed neural networks (PINNs) have proven an effective tool for solving differential equations, in particular when considering non-standard or ill-posed settings. When inferring solutions and parameters of the differential equation from data, uncertainty estimates are preferable to point estimates, as they give an idea about the accuracy of the solution. In this work, we consider the inverse problem and employ repulsive ensembles of PINNs (RE-PINN) for obtaining such estimates. The repulsion is implemented by adding a particular repulsive term to the loss function, which has the property that the ensemble predictions correspond to the true Bayesian posterior in the limit of infinite ensemble members. Where possible, we compare the ensemble predictions to Monte Carlo baselines. Whereas the standard ensemble tends to collapse to maximum-a-posteriori solutions, the repulsive ensemble produces significantly more accurate uncertainty estimates and exhibits higher sample diversity.

Probabilistic matching of real and generated data statistics in generative adversarial networks

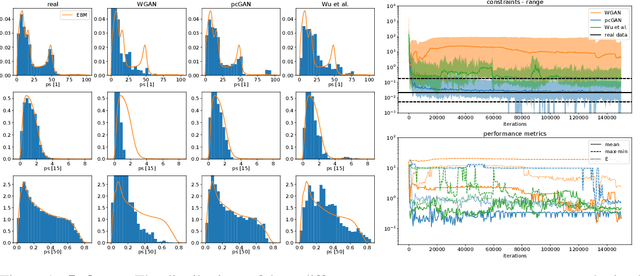
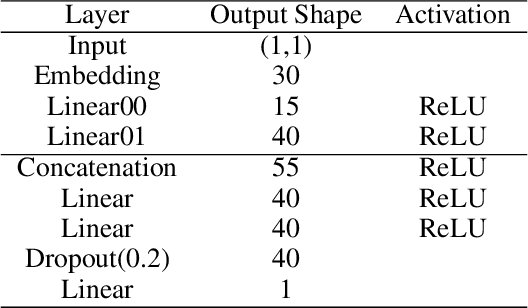
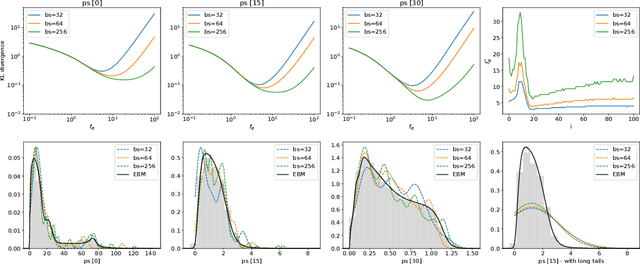
Generative adversarial networks constitute a powerful approach to generative modeling. While generated samples often are indistinguishable from real data, there is no guarantee that they will follow the true data distribution. In this work, we propose a method to ensure that the distributions of certain generated data statistics coincide with the respective distributions of the real data. In order to achieve this, we add a Kullback-Leibler term to the generator loss function: the KL divergence is taken between the true distributions as represented by a conditional energy-based model, and the corresponding generated distributions obtained from minibatch values at each iteration. We evaluate the method on a synthetic dataset and two real-world datasets and demonstrate improved performance of our method.

Physics-informed neural networks with unknown measurement noise

Physics-informed neural networks (PINNs) constitute a flexible approach to both finding solutions and identifying parameters of partial differential equations. Most works on the topic assume noiseless data, or data contaminated by weak Gaussian noise. We show that the standard PINN framework breaks down in case of non-Gaussian noise. We give a way of resolving this fundamental issue and we propose to jointly train an energy-based model (EBM) to learn the correct noise distribution. We illustrate the improved performance of our approach using multiple examples.

Incorporating Sum Constraints into Multitask Gaussian Processes

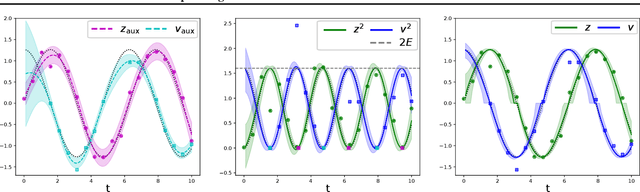
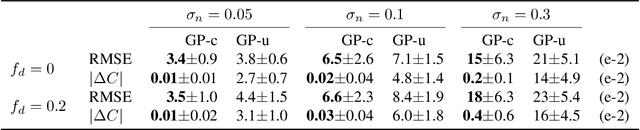
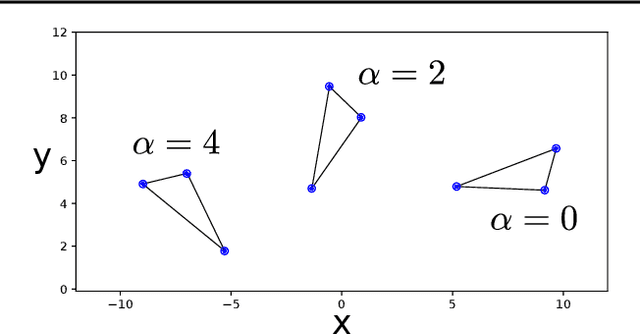
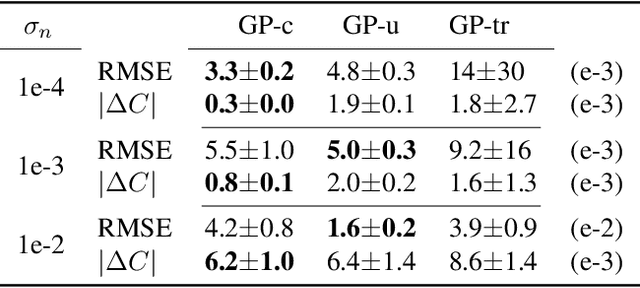
Machine learning models can be improved by adapting them to respect existing background knowledge. In this paper we consider multitask Gaussian processes, with background knowledge in the form of constraints that require a specific sum of the outputs to be constant. This is achieved by conditioning the prior distribution on the constraint fulfillment. The approach allows for both linear and nonlinear constraints. We demonstrate that the constraints are fulfilled with high precision and that the construction can improve the overall prediction accuracy as compared to the standard Gaussian process.