Variational State and Parameter Estimation

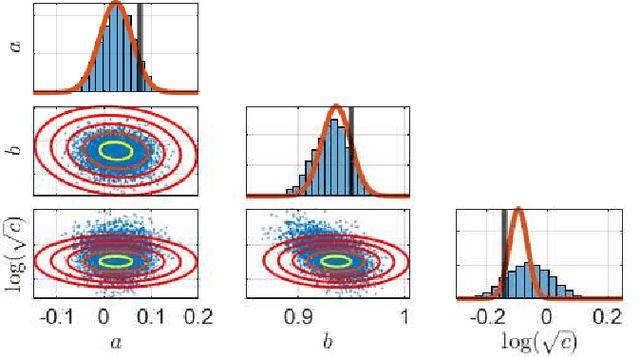
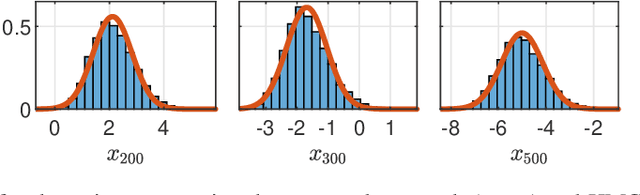
This paper considers the problem of computing Bayesian estimates of both states and model parameters for nonlinear state-space models. Generally, this problem does not have a tractable solution and approximations must be utilised. In this work, a variational approach is used to provide an assumed density which approximates the desired, intractable, distribution. The approach is deterministic and results in an optimisation problem of a standard form. Due to the parametrisation of the assumed density selected first- and second-order derivatives are readily available which allows for efficient solutions. The proposed method is compared against state-of-the-art Hamiltonian Monte Carlo in two numerical examples.

Linearly Constrained Neural Networks

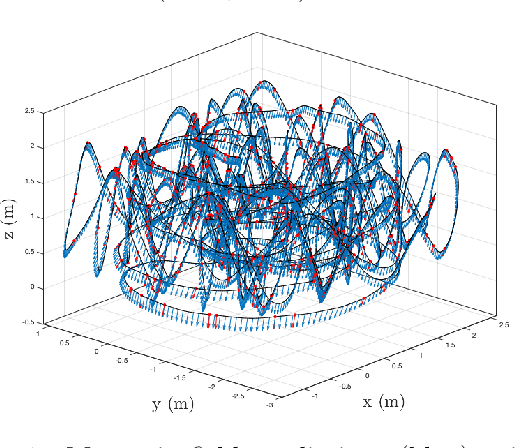
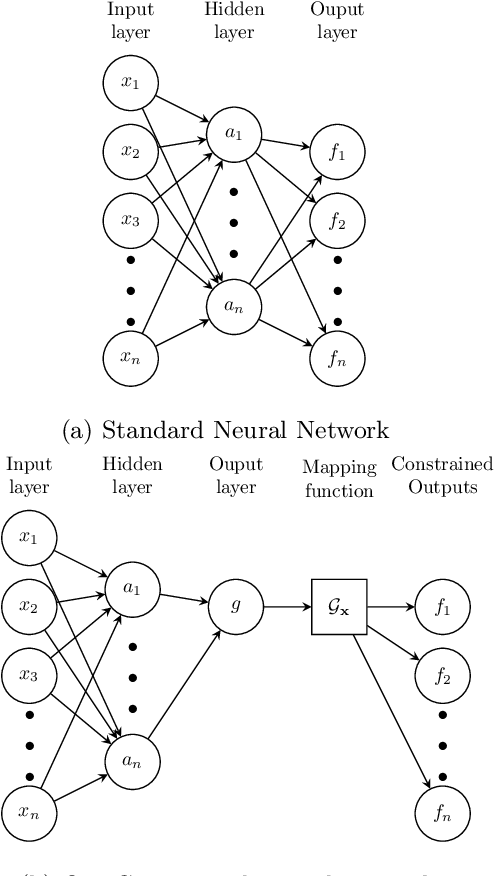
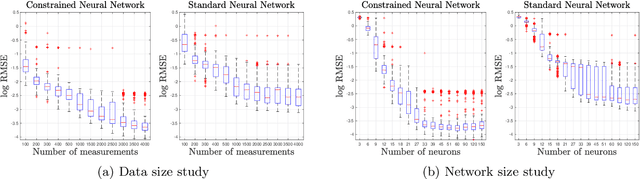
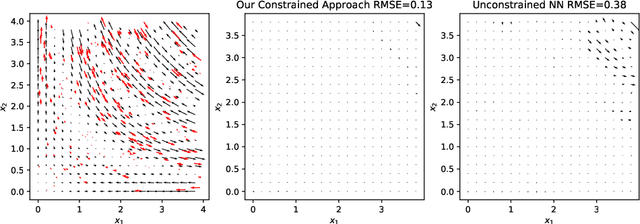
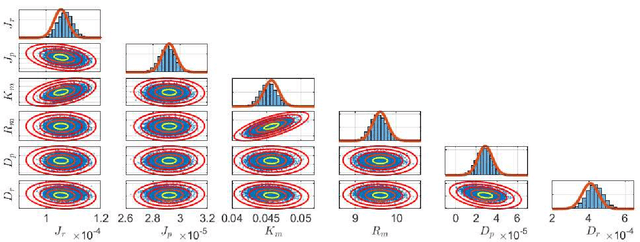
We present an approach to designing neural network based models that will explicitly satisfy known linear constraints. To achieve this, the target function is modelled as a linear transformation of an underlying function. This transformation is chosen such that any prediction of the target function is guaranteed to satisfy the constraints and can be determined from known physics or, more generally, by following a constructive procedure that was previously presented for Gaussian processes. The approach is demonstrated on simulated and real-data examples.

Deep kernel learning for integral measurements

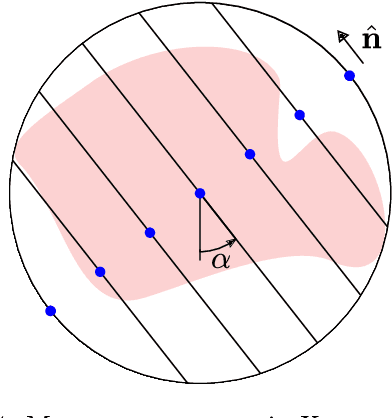
Deep kernel learning refers to a Gaussian process that incorporates neural networks to improve the modelling of complex functions. We present a method that makes this approach feasible for problems where the data consists of line integral measurements of the target function. The performance is illustrated on computed tomography reconstruction examples.

A Bayesian Filtering Algorithm for Gaussian Mixture Models

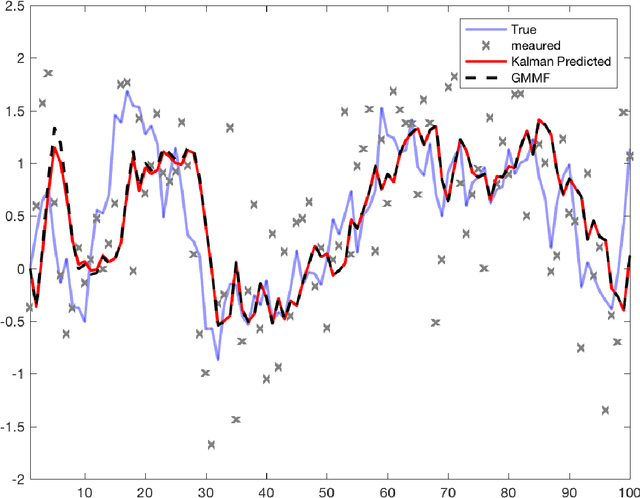
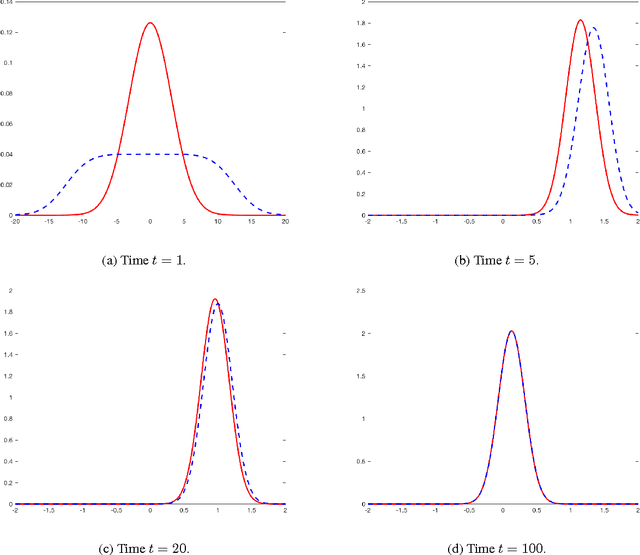
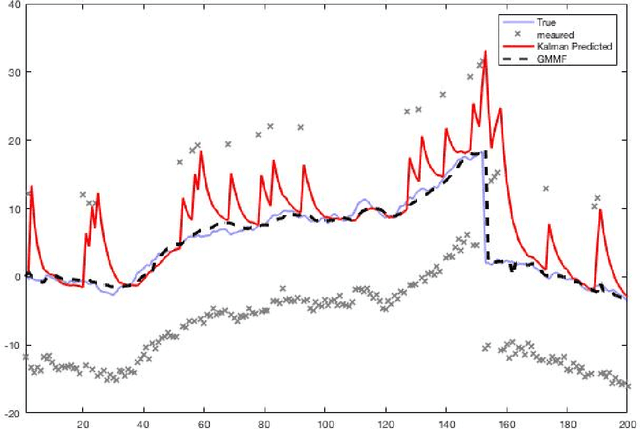
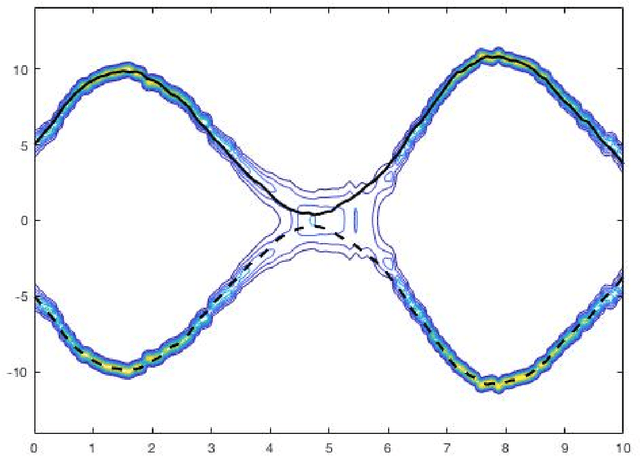
A Bayesian filtering algorithm is developed for a class of state-space systems that can be modelled via Gaussian mixtures. In general, the exact solution to this filtering problem involves an exponential growth in the number of mixture terms and this is handled here by utilising a Gaussian mixture reduction step after both the time and measurement updates. In addition, a square-root implementation of the unified algorithm is presented and this algorithm is profiled on several simulated systems. This includes the state estimation for two non-linear systems that are strictly outside the class considered in this paper.