RJHMC-Tree for Exploration of the Bayesian Decision Tree Posterior

Decision trees have found widespread application within the machine learning community due to their flexibility and interpretability. This paper is directed towards learning decision trees from data using a Bayesian approach, which is challenging due to the potentially enormous parameter space required to span all tree models. Several approaches have been proposed to combat this challenge, with one of the more successful being Markov chain Monte Carlo (MCMC) methods. The efficacy and efficiency of MCMC methods fundamentally rely on the quality of the so-called proposals, which is the focus of this paper. In particular, this paper investigates using a Hamiltonian Monte Carlo (HMC) approach to explore the posterior of Bayesian decision trees more efficiently by exploiting the geometry of the likelihood within a global update scheme. Two implementations of the novel algorithm are developed and compared to existing methods by testing against standard datasets in the machine learning and Bayesian decision tree literature. HMC-based methods are shown to perform favourably with respect to predictive test accuracy, acceptance rate, and tree complexity.

An Improved Random Matrix Prediction Model for Manoeuvring Extended Targets

This paper proposes an improved prediction update for extended target tracking with the random matrix model. A key innovation is to employ a generalised non-central inverse Wishart distribution to model the state transition density of the target extent; resulting in a prediction update that accounts for kinematic state dependent transformations. Moreover, the proposed prediction update offers an additional tuning parameter c.f. previous works, requires only a single Kullback-Leibler divergence minimisation, and improves overall target tracking performance when compared to state-of-the-art alternatives.

Beyond Occam's Razor in System Identification: Double-Descent when Modeling Dynamics

System identification aims to build models of dynamical systems from data. Traditionally, choosing the model requires the designer to balance between two goals of conflicting nature; the model must be rich enough to capture the system dynamics, but not so flexible that it learns spurious random effects from the dataset. It is typically observed that model validation performance follows a U-shaped curve as the model complexity increases. Recent developments in machine learning and statistics, however, have observed situations where a "double-descent" curve subsumes this U-shaped model-performance curve. With a second decrease in performance occurring beyond the point where the model has reached the capacity of interpolating - i.e., (near) perfectly fitting - the training data. To the best of our knowledge, however, such phenomena have not been studied within the context of the identification of dynamic systems. The present paper aims to answer the question: "Can such a phenomenon also be observed when estimating parameters of dynamic systems?" We show the answer is yes, verifying such behavior experimentally both for artificially generated and real-world datasets.

Deep Energy-Based NARX Models

This paper is directed towards the problem of learning nonlinear ARX models based on system input--output data. In particular, our interest is in learning a conditional distribution of the current output based on a finite window of past inputs and outputs. To achieve this, we consider the use of so-called energy-based models, which have been developed in allied fields for learning unknown distributions based on data. This energy-based model relies on a general function to describe the distribution, and here we consider a deep neural network for this purpose. The primary benefit of this approach is that it is capable of learning both simple and highly complex noise models, which we demonstrate on simulated and experimental data.

A Bayesian Filtering Algorithm for Gaussian Mixture Models

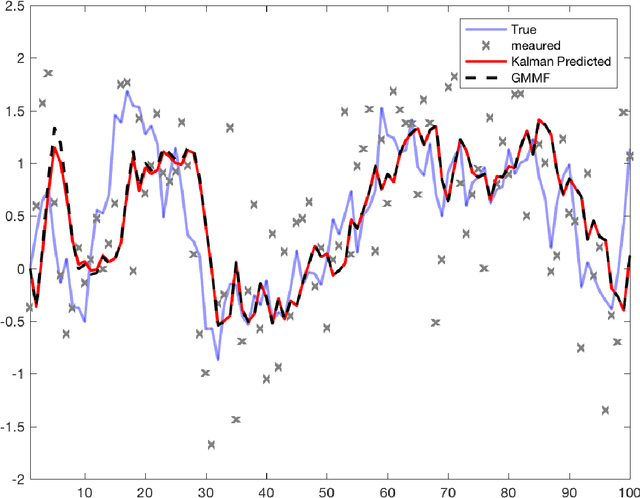
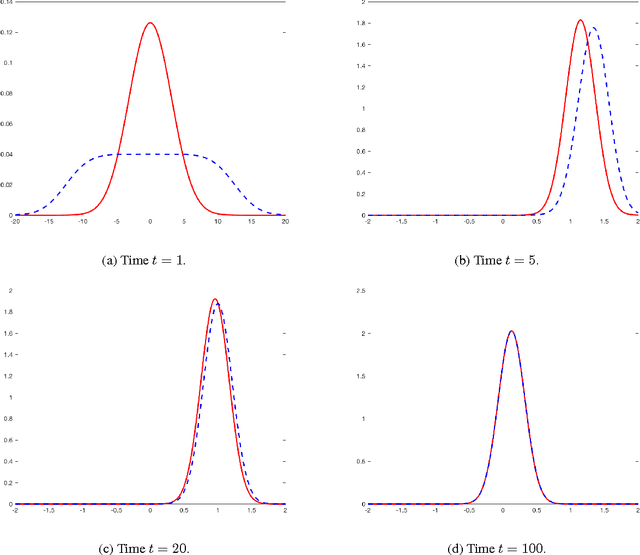
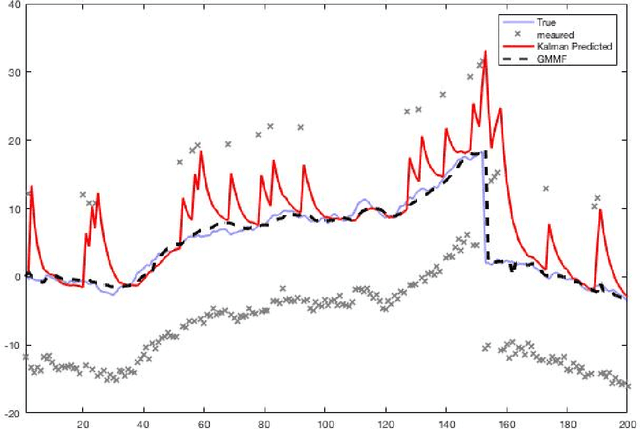
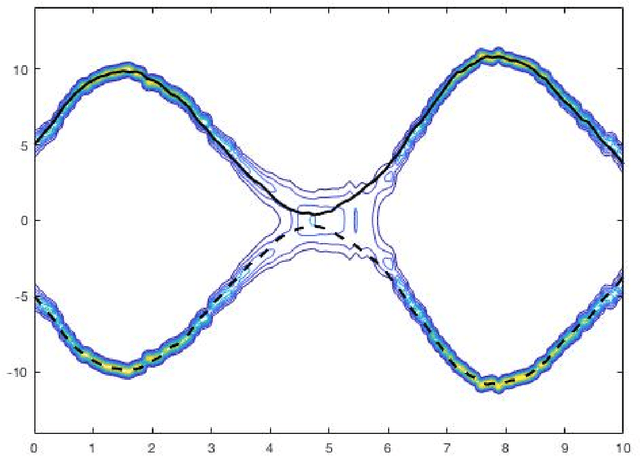
A Bayesian filtering algorithm is developed for a class of state-space systems that can be modelled via Gaussian mixtures. In general, the exact solution to this filtering problem involves an exponential growth in the number of mixture terms and this is handled here by utilising a Gaussian mixture reduction step after both the time and measurement updates. In addition, a square-root implementation of the unified algorithm is presented and this algorithm is profiled on several simulated systems. This includes the state estimation for two non-linear systems that are strictly outside the class considered in this paper.

On the construction of probabilistic Newton-type algorithms

It has recently been shown that many of the existing quasi-Newton algorithms can be formulated as learning algorithms, capable of learning local models of the cost functions. Importantly, this understanding allows us to safely start assembling probabilistic Newton-type algorithms, applicable in situations where we only have access to noisy observations of the cost function and its derivatives. This is where our interest lies. We make contributions to the use of the non-parametric and probabilistic Gaussian process models in solving these stochastic optimisation problems. Specifically, we present a new algorithm that unites these approximations together with recent probabilistic line search routines to deliver a probabilistic quasi-Newton approach. We also show that the probabilistic optimisation algorithms deliver promising results on challenging nonlinear system identification problems where the very nature of the problem is such that we can only access the cost function and its derivative via noisy observations, since there are no closed-form expressions available.