Jodie A. Cochrane
Divide, Conquer, Combine Bayesian Decision Tree Sampling
Mar 26, 2024

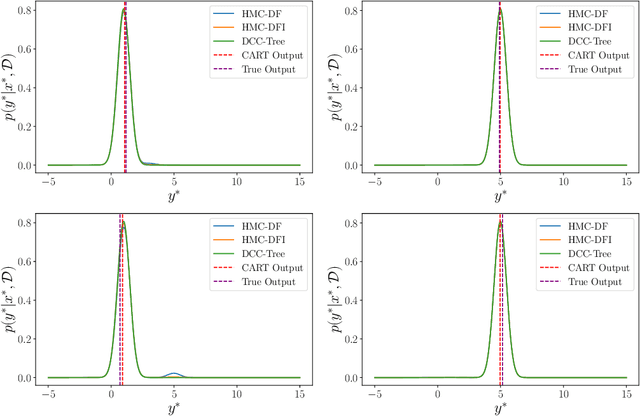

Abstract:Decision trees are commonly used predictive models due to their flexibility and interpretability. This paper is directed at quantifying the uncertainty of decision tree predictions by employing a Bayesian inference approach. This is challenging because these approaches need to explore both the tree structure space and the space of decision parameters associated with each tree structure. This has been handled by using Markov Chain Monte Carlo (MCMC) methods, where a Markov Chain is constructed to provide samples from the desired Bayesian estimate. Importantly, the structure and the decision parameters are tightly coupled; small changes in the tree structure can demand vastly different decision parameters to provide accurate predictions. A challenge for existing MCMC approaches is proposing joint changes in both the tree structure and the decision parameters that result in efficient sampling. This paper takes a different approach, where each distinct tree structure is associated with a unique set of decision parameters. The proposed approach, entitled DCC-Tree, is inspired by the work in Zhou et al. [23] for probabilistic programs and Cochrane et al. [4] for Hamiltonian Monte Carlo (HMC) based sampling for decision trees. Results show that DCC-Tree performs comparably to other HMC-based methods and better than existing Bayesian tree methods while improving on consistency and reducing the per-proposal complexity.
RJHMC-Tree for Exploration of the Bayesian Decision Tree Posterior
Dec 04, 2023Abstract:Decision trees have found widespread application within the machine learning community due to their flexibility and interpretability. This paper is directed towards learning decision trees from data using a Bayesian approach, which is challenging due to the potentially enormous parameter space required to span all tree models. Several approaches have been proposed to combat this challenge, with one of the more successful being Markov chain Monte Carlo (MCMC) methods. The efficacy and efficiency of MCMC methods fundamentally rely on the quality of the so-called proposals, which is the focus of this paper. In particular, this paper investigates using a Hamiltonian Monte Carlo (HMC) approach to explore the posterior of Bayesian decision trees more efficiently by exploiting the geometry of the likelihood within a global update scheme. Two implementations of the novel algorithm are developed and compared to existing methods by testing against standard datasets in the machine learning and Bayesian decision tree literature. HMC-based methods are shown to perform favourably with respect to predictive test accuracy, acceptance rate, and tree complexity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge