Variational State and Parameter Estimation

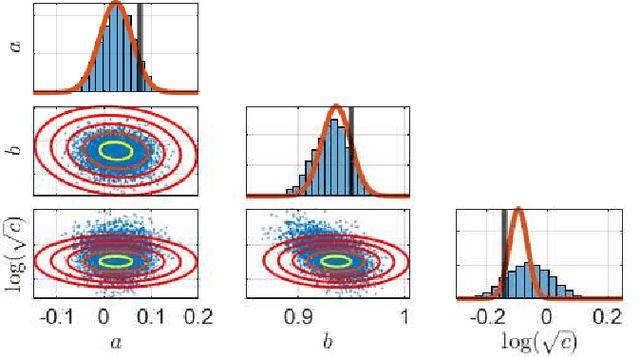
This paper considers the problem of computing Bayesian estimates of both states and model parameters for nonlinear state-space models. Generally, this problem does not have a tractable solution and approximations must be utilised. In this work, a variational approach is used to provide an assumed density which approximates the desired, intractable, distribution. The approach is deterministic and results in an optimisation problem of a standard form. Due to the parametrisation of the assumed density selected first- and second-order derivatives are readily available which allows for efficient solutions. The proposed method is compared against state-of-the-art Hamiltonian Monte Carlo in two numerical examples.

Variational Nonlinear System Identification

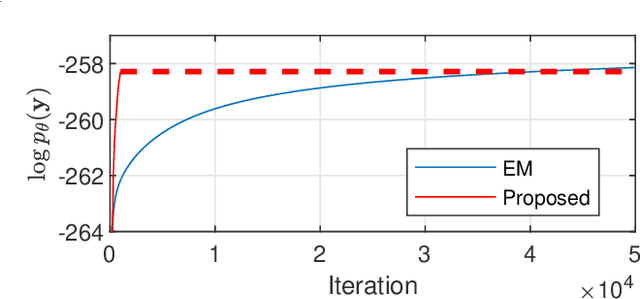
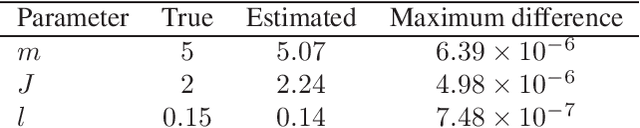
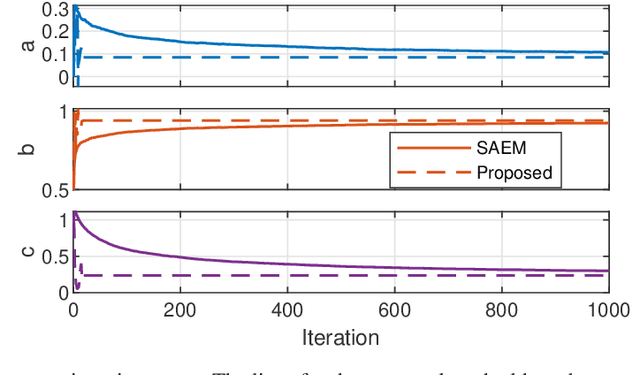
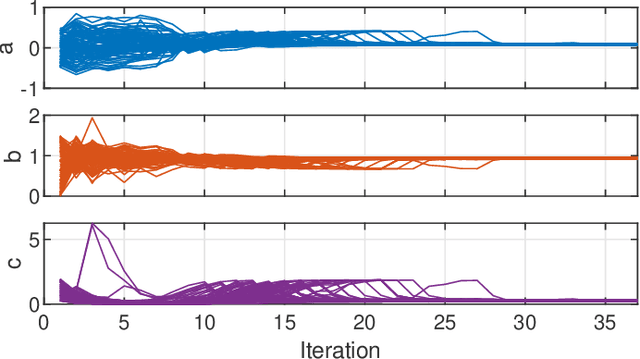
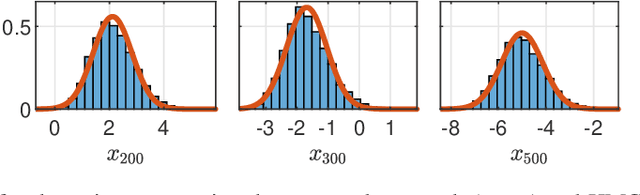
This paper considers parameter estimation for nonlinear state-space models, which is an important but challenging problem. We address this challenge by employing a variational inference (VI) approach, which is a principled method that has deep connections to maximum likelihood estimation. This VI approach ultimately provides estimates of the model as solutions to an optimisation problem, which is deterministic, tractable and can be solved using standard optimisation tools. A specialisation of this approach for systems with additive Gaussian noise is also detailed. The proposed method is examined numerically on a range of simulation and real examples with a focus on robustness to parameter initialisations; we additionally perform favourable comparisons against state-of-the-art alternatives.

Constructing a variational family for nonlinear state-space models

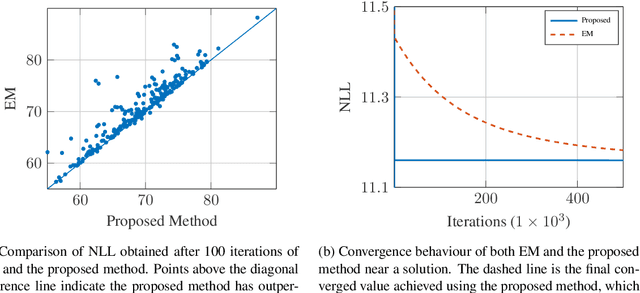
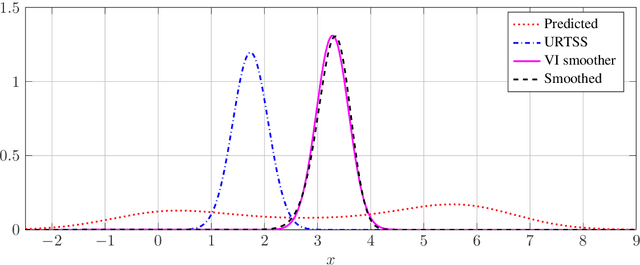
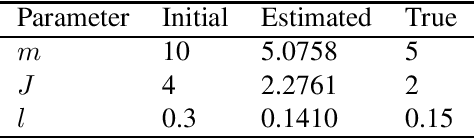
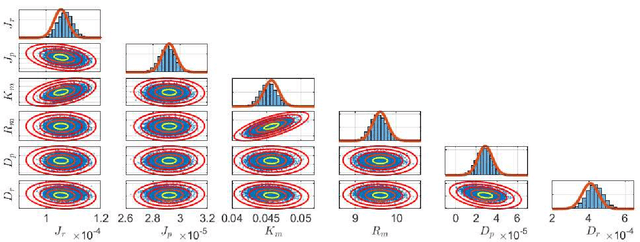
We consider the problem of maximum likelihood parameter estimation for nonlinear state-space models. This is an important, but challenging problem. This challenge stems from the intractable multidimensional integrals that must be solved in order to compute, and maximise, the likelihood. Here we present a new variational family where variational inference is used in combination with tractable approximations of these integrals resulting in a deterministic optimisation problem. Our developments also include a novel means for approximating the smoothed state distributions. We demonstrate our construction on several examples and show that they perform well compared to state of the art methods on real data-sets.