A Probabilistically Motivated Learning Rate Adaptation for Stochastic Optimization
Paper and Code
Feb 22, 2021
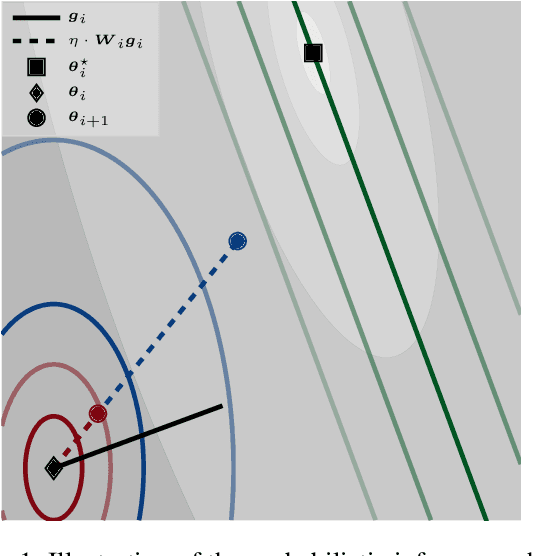
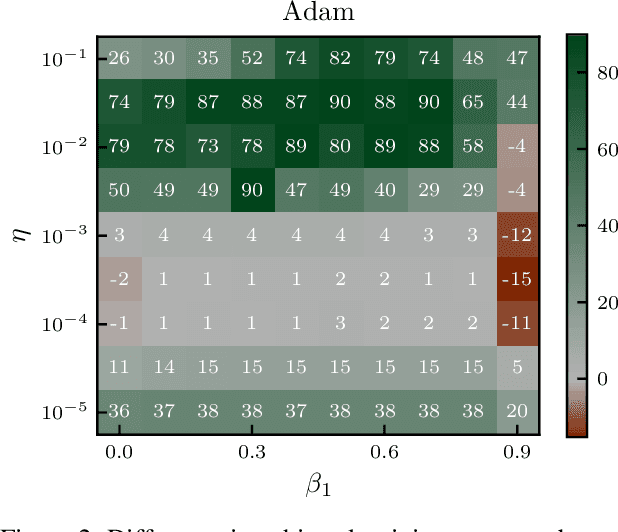
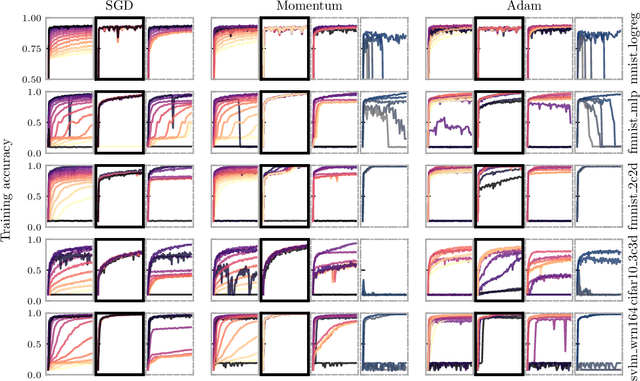
Machine learning practitioners invest significant manual and computational resources in finding suitable learning rates for optimization algorithms. We provide a probabilistic motivation, in terms of Gaussian inference, for popular stochastic first-order methods. As an important special case, it recovers the Polyak step with a general metric. The inference allows us to relate the learning rate to a dimensionless quantity that can be automatically adapted during training by a control algorithm. The resulting meta-algorithm is shown to adapt learning rates in a robust manner across a large range of initial values when applied to deep learning benchmark problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge