Variational Elliptical Processes

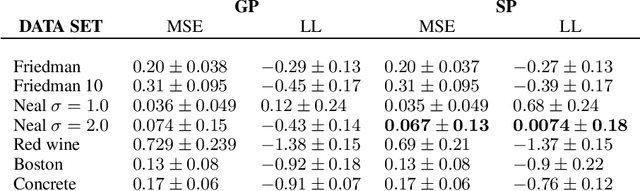
We present elliptical processes, a family of non-parametric probabilistic models that subsume Gaussian processes and Student's t processes. This generalization includes a range of new heavy-tailed behaviors while retaining computational tractability. Elliptical processes are based on a representation of elliptical distributions as a continuous mixture of Gaussian distributions. We parameterize this mixture distribution as a spline normalizing flow, which we train using variational inference. The proposed form of the variational posterior enables a sparse variational elliptical process applicable to large-scale problems. We highlight advantages compared to Gaussian processes through regression and classification experiments. Elliptical processes can supersede Gaussian processes in several settings, including cases where the likelihood is non-Gaussian or when accurate tail modeling is essential.

The Elliptical Processes: a New Family of Flexible Stochastic Processes

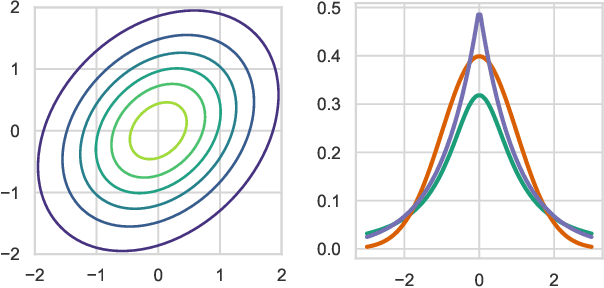
We present the elliptical processes-a new family of stochastic processes that subsumes the Gaussian process and the Student-t process. This generalization retains computational tractability while substantially increasing the range of tail behaviors that can be modeled. We base the elliptical processes on a representation of elliptical distributions as mixtures of Gaussian distributions and derive closed-form expressions for the marginal and conditional distributions. We perform an in-depth study of a particular elliptical process, where the mixture distribution is piecewise constant, and show some of its advantages over the Gaussian process through a number of experiments on robust regression. Looking forward, we believe there are several settings, e.g. when the likelihood is not Gaussian or when accurate tail modeling is critical, where the elliptical processes could become the stochastic processes of choice.

The NIGENS General Sound Events Database

Computational auditory scene analysis is gaining interest in the last years. Trailing behind the more mature field of speech recognition, it is particularly general sound event detection that is attracting increasing attention. Crucial for training and testing reasonable models is having available enough suitable data -- until recently, general sound event databases were hardly found. We release and present a database with 714 wav files containing isolated high quality sound events of 14 different types, plus 303 `general' wav files of anything else but these 14 types. All sound events are strongly labeled with perceptual on- and offset times, paying attention to omitting in-between silences. The amount of isolated sound events, the quality of annotations, and the particular general sound class distinguish NIGENS from other databases.

On the Convergence of Extended Variational Inference for Non-Gaussian Statistical Models

Variational inference (VI) is a widely used framework in Bayesian estimation. For most of the non-Gaussian statistical models, it is infeasible to find an analytically tractable solution to estimate the posterior distributions of the parameters. Recently, an improved framework, namely the extended variational inference (EVI), has been introduced and applied to derive analytically tractable solution by employing lower-bound approximation to the variational objective function. Two conditions required for EVI implementation, namely the weak condition and the strong condition, are discussed and compared in this paper. In practical implementation, the convergence of the EVI depends on the selection of the lower-bound approximation, no matter with the weak condition or the strong condition. In general, two approximation strategies, the single lower-bound (SLB) approximation and the multiple lower-bounds (MLB) approximation, can be applied to carry out the lower-bound approximation. To clarify the differences between the SLB and the MLB, we will also discuss the convergence properties of the aforementioned two approximations. Extensive comparisons are made based on some existing EVI-based non-Gaussian statistical models. Theoretical analysis are conducted to demonstrate the differences between the weak and the strong conditions. Qualitative and quantitative experimental results are presented to show the advantages of the SLB approximation.

Constructing the Matrix Multilayer Perceptron and its Application to the VAE

Like most learning algorithms, the multilayer perceptrons (MLP) is designed to learn a vector of parameters from data. However, in certain scenarios we are interested in learning structured parameters (predictions) in the form of symmetric positive definite matrices. Here, we introduce a variant of the MLP, referred to as the matrix MLP, that is specialized at learning symmetric positive definite matrices. We also present an application of the model within the context of the variational autoencoder (VAE). Our formulation of the VAE extends the vanilla formulation to the cases where the recognition and the generative networks can be from the parametric family of distributions with dense covariance matrices. Two specific examples are discussed in more detail: the dense covariance Gaussian and its generalization, the power exponential distribution. Our new developments are illustrated using both synthetic and real data.

Conditionally Independent Multiresolution Gaussian Processes

We propose a multiresolution Gaussian process (GP) model which assumes conditional independence among GPs across resolutions. The model is built on the hierarchical application of predictive processes using a particular representation of the GP via the Karhunen-Loeve expansion with a Bingham prior model, where each basis vector of the expansion consists of an axis and a scale factor, referred to as the basis axis and the basis-axis scale. The basis axes have unique characteristics: They are zero-mean by construction and live on the unit sphere. These properties allow us to further assume that the axes are shared across all resolutions while their scales remain resolution specific. The properties of the Bingham distribution makes it the natural choice when it comes to modeling the axes. We drive a fully Bayesian inference for the model using a structured variational inference with a partially factorized mean-field approximation which learns a joint Gaussian-Bingham posterior distribution over the basis-axis scales and the basis axes. Relaxing the full independence assumption enables the construction of models which are robust to overfitting in the sense of sensitivity to the chosen resolution and predictions that are smooth at the boundaries. Our new model and inference algorithm are compared against current state of the art on 2 synthetic and 9 real-world datasets.