Applying Deep Reinforcement Learning to the HP Model for Protein Structure Prediction

A central problem in computational biophysics is protein structure prediction, i.e., finding the optimal folding of a given amino acid sequence. This problem has been studied in a classical abstract model, the HP model, where the protein is modeled as a sequence of H (hydrophobic) and P (polar) amino acids on a lattice. The objective is to find conformations maximizing H-H contacts. It is known that even in this reduced setting, the problem is intractable (NP-hard). In this work, we apply deep reinforcement learning (DRL) to the two-dimensional HP model. We can obtain the conformations of best known energies for benchmark HP sequences with lengths from 20 to 50. Our DRL is based on a deep Q-network (DQN). We find that a DQN based on long short-term memory (LSTM) architecture greatly enhances the RL learning ability and significantly improves the search process. DRL can sample the state space efficiently, without the need of manual heuristics. Experimentally we show that it can find multiple distinct best-known solutions per trial. This study demonstrates the effectiveness of deep reinforcement learning in the HP model for protein folding.

Sequential Monte Carlo Methods for System Identification

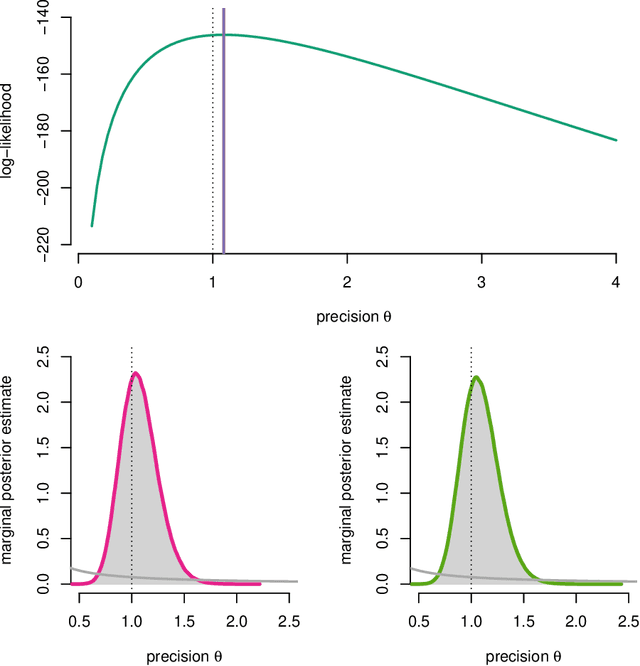
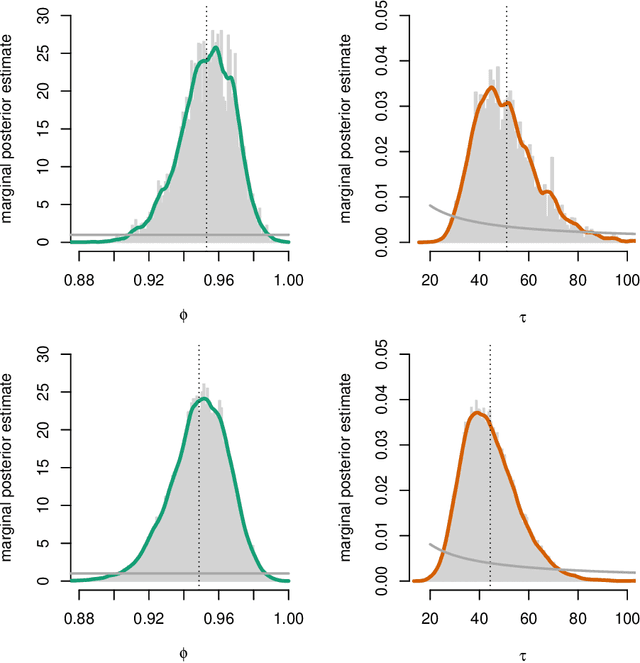
One of the key challenges in identifying nonlinear and possibly non-Gaussian state space models (SSMs) is the intractability of estimating the system state. Sequential Monte Carlo (SMC) methods, such as the particle filter (introduced more than two decades ago), provide numerical solutions to the nonlinear state estimation problems arising in SSMs. When combined with additional identification techniques, these algorithms provide solid solutions to the nonlinear system identification problem. We describe two general strategies for creating such combinations and discuss why SMC is a natural tool for implementing these strategies.

Sparse Estimation From Noisy Observations of an Overdetermined Linear System

This note studies a method for the efficient estimation of a finite number of unknown parameters from linear equations, which are perturbed by Gaussian noise. In case the unknown parameters have only few nonzero entries, the proposed estimator performs more efficiently than a traditional approach. The method consists of three steps: (1) a classical Least Squares Estimate (LSE), (2) the support is recovered through a Linear Programming (LP) optimization problem which can be computed using a soft-thresholding step, (3) a de-biasing step using a LSE on the estimated support set. The main contribution of this note is a formal derivation of an associated ORACLE property of the final estimate. That is, when the number of samples is large enough, the estimate is shown to equal the LSE based on the support of the {\em true} parameters.