Fast Converging Anytime Model Counting

Model counting is a fundamental problem which has been influential in many applications, from artificial intelligence to formal verification. Due to the intrinsic hardness of model counting, approximate techniques have been developed to solve real-world instances of model counting. This paper designs a new anytime approach called PartialKC for approximate model counting. The idea is a form of partial knowledge compilation to provide an unbiased estimate of the model count which can converge to the exact count. Our empirical analysis demonstrates that PartialKC achieves significant scalability and accuracy over prior state-of-the-art approximate counters, including satss and STS. Interestingly, the empirical results show that PartialKC reaches convergence for many instances and therefore provides exact model counting performance comparable to state-of-the-art exact counters.

Applying Deep Reinforcement Learning to the HP Model for Protein Structure Prediction

A central problem in computational biophysics is protein structure prediction, i.e., finding the optimal folding of a given amino acid sequence. This problem has been studied in a classical abstract model, the HP model, where the protein is modeled as a sequence of H (hydrophobic) and P (polar) amino acids on a lattice. The objective is to find conformations maximizing H-H contacts. It is known that even in this reduced setting, the problem is intractable (NP-hard). In this work, we apply deep reinforcement learning (DRL) to the two-dimensional HP model. We can obtain the conformations of best known energies for benchmark HP sequences with lengths from 20 to 50. Our DRL is based on a deep Q-network (DQN). We find that a DQN based on long short-term memory (LSTM) architecture greatly enhances the RL learning ability and significantly improves the search process. DRL can sample the state space efficiently, without the need of manual heuristics. Experimentally we show that it can find multiple distinct best-known solutions per trial. This study demonstrates the effectiveness of deep reinforcement learning in the HP model for protein folding.

CCDD: A Tractable Representation for Model Counting and Uniform Sampling

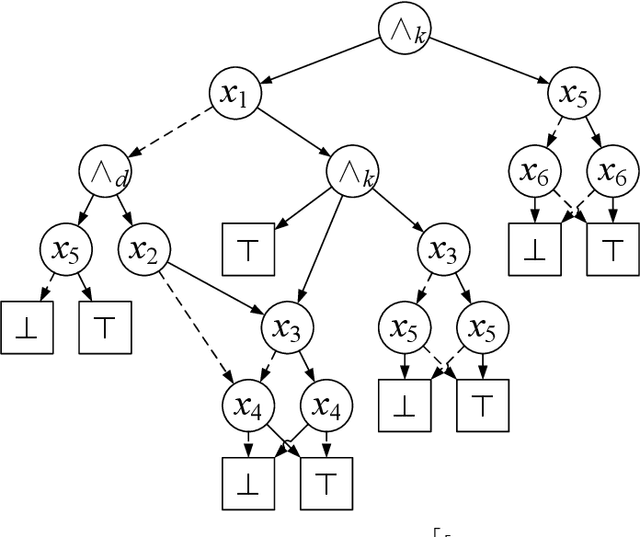
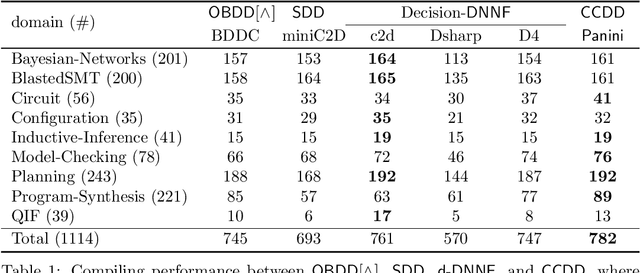
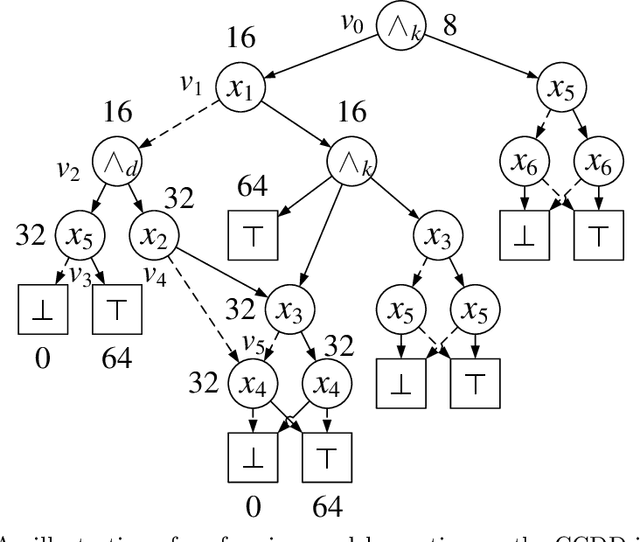
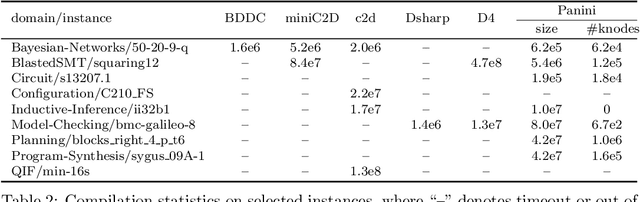
Knowledge compilation concerns with the compilation of representation languages to target languages supporting a wide range of tractable operations arising from diverse areas of computer science. Tractable target compilation languages are usually achieved by restrictions on the internal nodes of the NNF. In this paper, we propose a new representation language CCDD, which introduces new restrictions on conjunction nodes to capture equivalent literals. We show that CCDD supports two key queries, model counting and uniform samping, in polytime. We present algorithms and a compiler to compile propositional formulas expressed in CNF into CCDD. Experiments over a large set of benchmarks show that our compilation times are better with smaller representation than state-of-art Decision-DNNF, SDD and OBDD[AND] compilers. We apply our techniques to model counting and uniform sampling, and develop model counter and uniform sampler on CNF. Our empirical evaluation demonstrates the following significant improvements: our model counter can solve 885 instances while the prior state of the art solved only 843 instances, representing an improvement of 43 instances; and our uniform sampler can solve 780 instances while the prior state of the art solved only 648 instances, representing an improvement of 132 instances.

Benchmarking Symbolic Execution Using Constraint Problems -- Initial Results

Symbolic execution is a powerful technique for bug finding and program testing. It is successful in finding bugs in real-world code. The core reasoning techniques use constraint solving, path exploration, and search, which are also the same techniques used in solving combinatorial problems, e.g., finite-domain constraint satisfaction problems (CSPs). We propose CSP instances as more challenging benchmarks to evaluate the effectiveness of the core techniques in symbolic execution. We transform CSP benchmarks into C programs suitable for testing the reasoning capabilities of symbolic execution tools. From a single CSP P, we transform P depending on transformation choice into different C programs. Preliminary testing with the KLEE, Tracer-X, and LLBMC tools show substantial runtime differences from transformation and solver choice. Our C benchmarks are effective in showing the limitations of existing symbolic execution tools. The motivation for this work is we believe that benchmarks of this form can spur the development and engineering of improved core reasoning in symbolic execution engines.

Correlation Heuristics for Constraint Programming

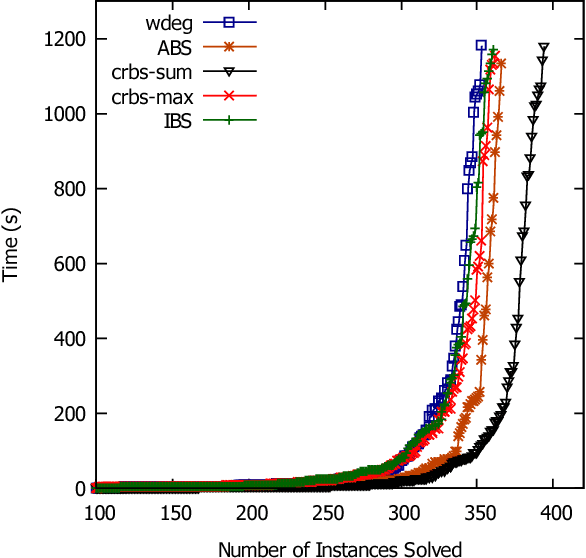
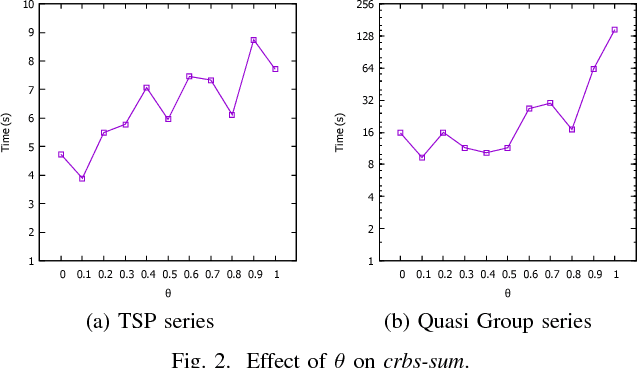
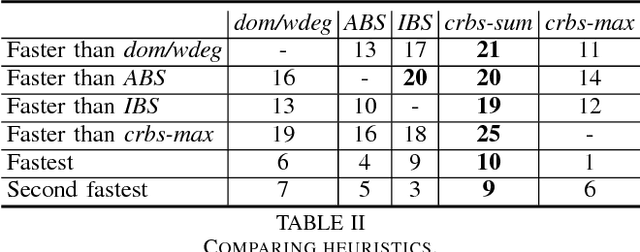
Effective general-purpose search strategies are an important component in Constraint Programming. We introduce a new idea, namely, using correlations between variables to guide search. Variable correlations are measured and maintained by using domain changes during constraint propagation. We propose two variable heuristics based on the correlation matrix, crbs-sum and crbs-max. We evaluate our correlation heuristics with well known heuristics, namely, dom/wdeg, impact-based search and activity-based search. Experiments on a large set of benchmarks show that our correlation heuristics are competitive with the other heuristics, and can be the fastest on many series.

Learning Robust Search Strategies Using a Bandit-Based Approach

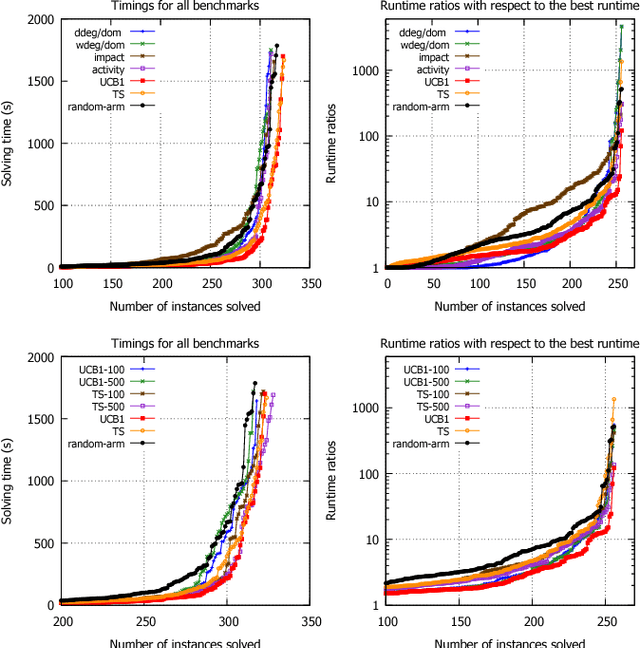
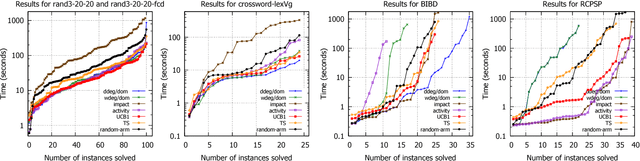
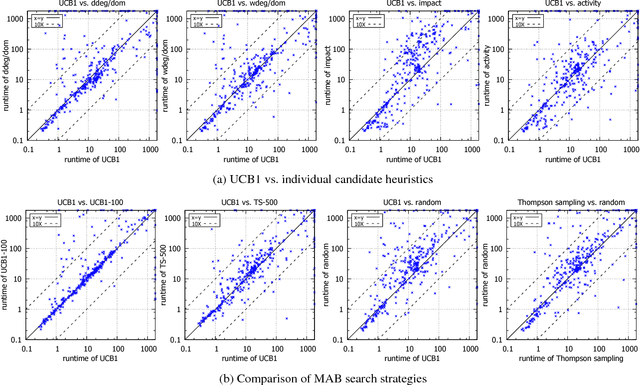
Effective solving of constraint problems often requires choosing good or specific search heuristics. However, choosing or designing a good search heuristic is non-trivial and is often a manual process. In this paper, rather than manually choosing/designing search heuristics, we propose the use of bandit-based learning techniques to automatically select search heuristics. Our approach is online where the solver learns and selects from a set of heuristics during search. The goal is to obtain automatic search heuristics which give robust performance. Preliminary experiments show that our adaptive technique is more robust than the original search heuristics. It can also outperform the original heuristics.

Solving Functional Constraints by Variable Substitution

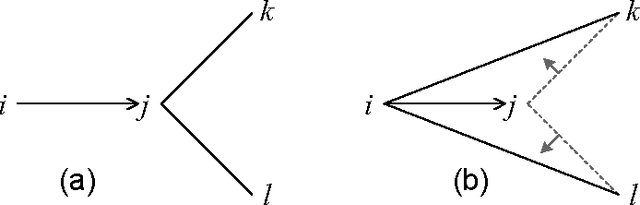
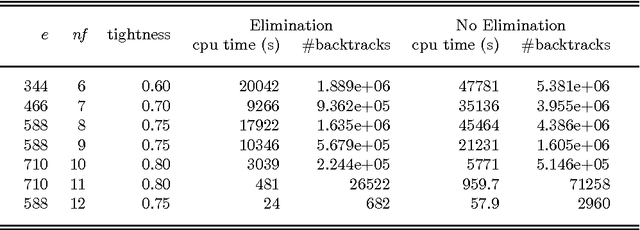
Functional constraints and bi-functional constraints are an important constraint class in Constraint Programming (CP) systems, in particular for Constraint Logic Programming (CLP) systems. CP systems with finite domain constraints usually employ CSP-based solvers which use local consistency, for example, arc consistency. We introduce a new approach which is based instead on variable substitution. We obtain efficient algorithms for reducing systems involving functional and bi-functional constraints together with other non-functional constraints. It also solves globally any CSP where there exists a variable such that any other variable is reachable from it through a sequence of functional constraints. Our experiments on random problems show that variable elimination can significantly improve the efficiency of solving problems with functional constraints.

Towards "Propagation = Logic + Control"

Constraint propagation algorithms implement logical inference. For efficiency, it is essential to control whether and in what order basic inference steps are taken. We provide a high-level framework that clearly differentiates between information needed for controlling propagation versus that needed for the logical semantics of complex constraints composed from primitive ones. We argue for the appropriateness of our controlled propagation framework by showing that it captures the underlying principles of manually designed propagation algorithms, such as literal watching for unit clause propagation and the lexicographic ordering constraint. We provide an implementation and benchmark results that demonstrate the practicality and efficiency of our framework.