Solving Functional Constraints by Variable Substitution
Paper and Code
Jun 16, 2010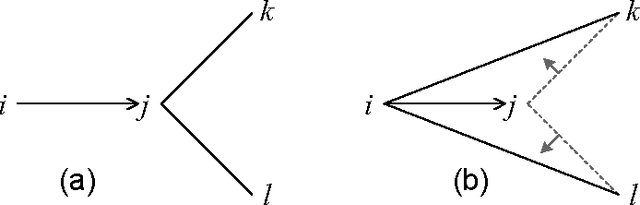


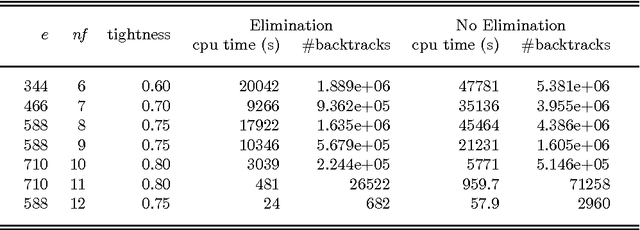
Functional constraints and bi-functional constraints are an important constraint class in Constraint Programming (CP) systems, in particular for Constraint Logic Programming (CLP) systems. CP systems with finite domain constraints usually employ CSP-based solvers which use local consistency, for example, arc consistency. We introduce a new approach which is based instead on variable substitution. We obtain efficient algorithms for reducing systems involving functional and bi-functional constraints together with other non-functional constraints. It also solves globally any CSP where there exists a variable such that any other variable is reachable from it through a sequence of functional constraints. Our experiments on random problems show that variable elimination can significantly improve the efficiency of solving problems with functional constraints.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge