Relation Variables in Qualitative Spatial Reasoning

We study an alternative to the prevailing approach to modelling qualitative spatial reasoning (QSR) problems as constraint satisfaction problems. In the standard approach, a relation between objects is a constraint whereas in the alternative approach it is a variable. The relation-variable approach greatly simplifies integration and implementation of QSR. To substantiate this point, we discuss several QSR algorithms from the literature which in the relation-variable approach reduce to the customary constraint propagation algorithm enforcing generalised arc-consistency.

Infinite Qualitative Simulations by Means of Constraint Programming

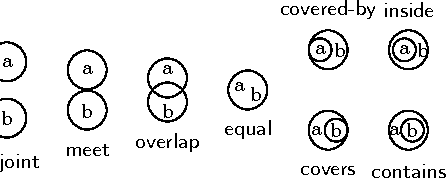
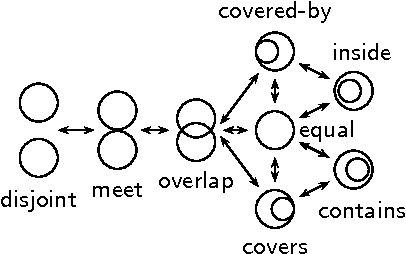
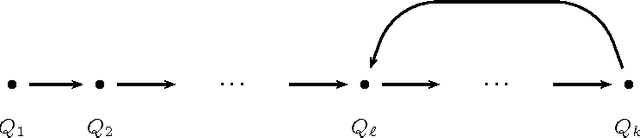
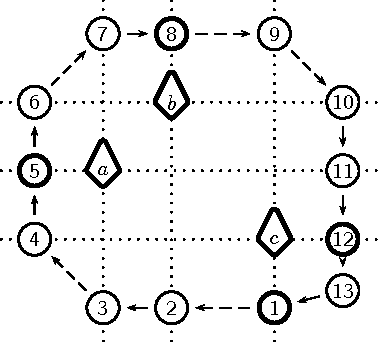
We introduce a constraint-based framework for studying infinite qualitative simulations concerned with contingencies such as time, space, shape, size, abstracted into a finite set of qualitative relations. To define the simulations, we combine constraints that formalize the background knowledge concerned with qualitative reasoning with appropriate inter-state constraints that are formulated using linear temporal logic. We implemented this approach in a constraint programming system by drawing on ideas from bounded model checking. The resulting system allows us to test and modify the problem specifications in a straightforward way and to combine various knowledge aspects.

Towards "Propagation = Logic + Control"

Constraint propagation algorithms implement logical inference. For efficiency, it is essential to control whether and in what order basic inference steps are taken. We provide a high-level framework that clearly differentiates between information needed for controlling propagation versus that needed for the logical semantics of complex constraints composed from primitive ones. We argue for the appropriateness of our controlled propagation framework by showing that it captures the underlying principles of manually designed propagation algorithms, such as literal watching for unit clause propagation and the lexicographic ordering constraint. We provide an implementation and benchmark results that demonstrate the practicality and efficiency of our framework.

Constraint-Based Qualitative Simulation

We consider qualitative simulation involving a finite set of qualitative relations in presence of complete knowledge about their interrelationship. We show how it can be naturally captured by means of constraints expressed in temporal logic and constraint satisfaction problems. The constraints relate at each stage the 'past' of a simulation with its 'future'. The benefit of this approach is that it readily leads to an implementation based on constraint technology that can be used to generate simulations and to answer queries about them.