Open Problems in a Logic of Gossips

Gossip protocols are programs used in a setting in which each agent holds a secret and the aim is to reach a situation in which all agents know all secrets. Such protocols rely on a point-to-point or group communication. Distributed epistemic gossip protocols use epistemic formulas in the component programs for the agents. The advantage of the use of epistemic logic is that the resulting protocols are very concise and amenable for a simple verification. Recently, we introduced a natural modal logic that allows one to express distributed epistemic gossip protocols and to reason about their correctness. We proved that the resulting protocols are implementable and that all aspects of their correctness, including termination, are decidable. To establish these results we showed that both the definition of semantics and of truth of the underlying logic are decidable. We also showed that the analogous results hold for an extension of this logic with the 'common knowledge' operator. However, several, often deceptively simple, questions about this logic and the corresponding gossip protocols remain open. The purpose of this paper is to list and elucidate these questions and provide for them an appropriate background information in the form of partial of related results.

Common Knowledge in a Logic of Gossips

Gossip protocols aim at arriving, by means of point-to-point or group communications, at a situation in which all the agents know each other secrets. Recently a number of authors studied distributed epistemic gossip protocols. These protocols use as guards formulas from a simple epistemic logic, which makes their analysis and verification substantially easier. We study here common knowledge in the context of such a logic. First, we analyze when it can be reduced to iterated knowledge. Then we show that the semantics and truth for formulas without nested common knowledge operator are decidable. This implies that implementability, partial correctness and termination of distributed epistemic gossip protocols that use non-nested common knowledge operator is decidable, as well. Given that common knowledge is equivalent to an infinite conjunction of nested knowledge, these results are non-trivial generalizations of the corresponding decidability results for the original epistemic logic, established in (Apt & Wojtczak, 2016). K. R. Apt & D. Wojtczak (2016): On Decidability of a Logic of Gossips. In Proc. of JELIA 2016, pp. 18-33, doi:10.1007/ 978-3-319-48758-8_2.

Epistemic Protocols for Distributed Gossiping

Gossip protocols aim at arriving, by means of point-to-point or group communications, at a situation in which all the agents know each other's secrets. We consider distributed gossip protocols which are expressed by means of epistemic logic. We provide an operational semantics of such protocols and set up an appropriate framework to argue about their correctness. Then we analyze specific protocols for complete graphs and for directed rings.

A comparison of the notions of optimality in soft constraints and graphical games

The notion of optimality naturally arises in many areas of applied mathematics and computer science concerned with decision making. Here we consider this notion in the context of two formalisms used for different purposes and in different research areas: graphical games and soft constraints. We relate the notion of optimality used in the area of soft constraint satisfaction problems (SCSPs) to that used in graphical games, showing that for a large class of SCSPs that includes weighted constraints every optimal solution corresponds to a Nash equilibrium that is also a Pareto efficient joint strategy.

Comparing the notions of optimality in CP-nets, strategic games and soft constraints

The notion of optimality naturally arises in many areas of applied mathematics and computer science concerned with decision making. Here we consider this notion in the context of three formalisms used for different purposes in reasoning about multi-agent systems: strategic games, CP-nets, and soft constraints. To relate the notions of optimality in these formalisms we introduce a natural qualitative modification of the notion of a strategic game. We show then that the optimal outcomes of a CP-net are exactly the Nash equilibria of such games. This allows us to use the techniques of game theory to search for optimal outcomes of CP-nets and vice-versa, to use techniques developed for CP-nets to search for Nash equilibria of the considered games. Then, we relate the notion of optimality used in the area of soft constraints to that used in a generalization of strategic games, called graphical games. In particular we prove that for a natural class of soft constraints that includes weighted constraints every optimal solution is both a Nash equilibrium and Pareto efficient joint strategy. For a natural mapping in the other direction we show that Pareto efficient joint strategies coincide with the optimal solutions of soft constraints.

Epistemic Analysis of Strategic Games with Arbitrary Strategy Sets

We provide here an epistemic analysis of arbitrary strategic games based on the possibility correspondences. Such an analysis calls for the use of transfinite iterations of the corresponding operators. Our approach is based on Tarski's Fixpoint Theorem and applies both to the notions of rationalizability and the iterated elimination of strictly dominated strategies.

An Analysis of Arithmetic Constraints on Integer Intervals

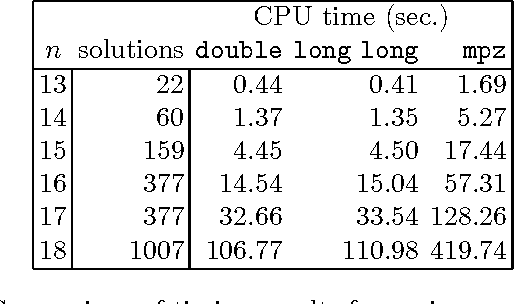
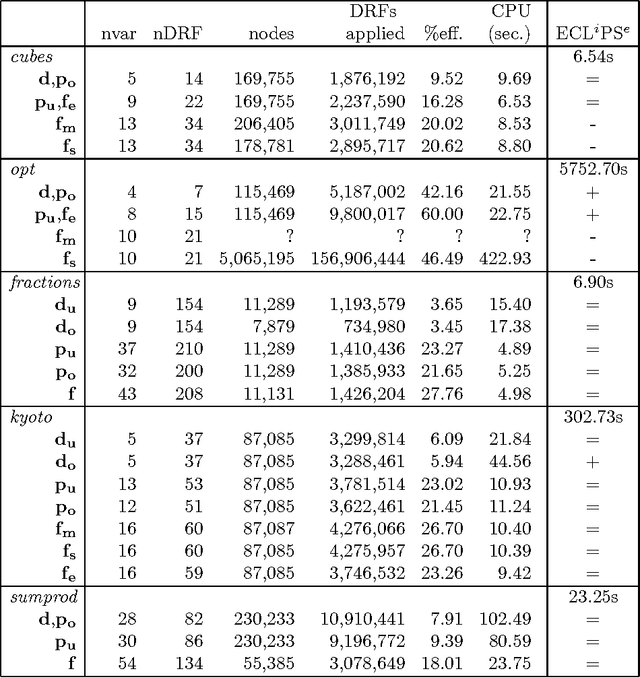
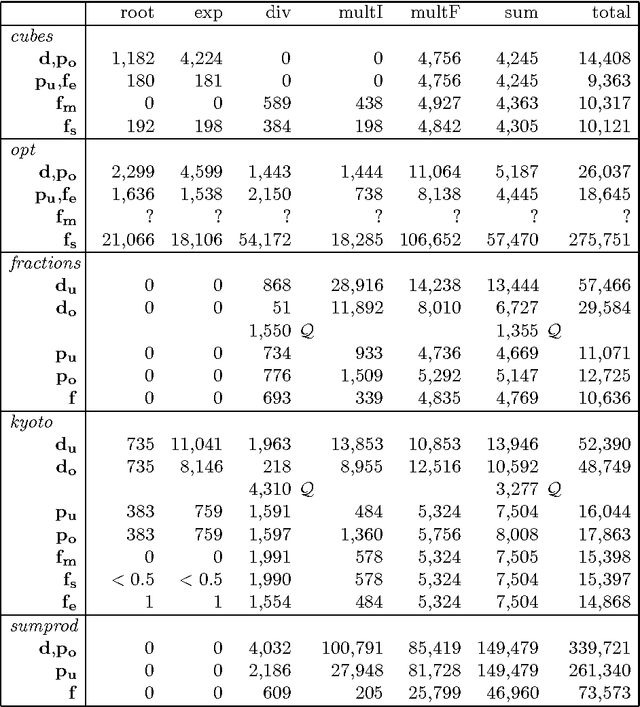
Arithmetic constraints on integer intervals are supported in many constraint programming systems. We study here a number of approaches to implement constraint propagation for these constraints. To describe them we introduce integer interval arithmetic. Each approach is explained using appropriate proof rules that reduce the variable domains. We compare these approaches using a set of benchmarks. For the most promising approach we provide results that characterize the effect of constraint propagation. This is a full version of our earlier paper, cs.PL/0403016.

Infinite Qualitative Simulations by Means of Constraint Programming

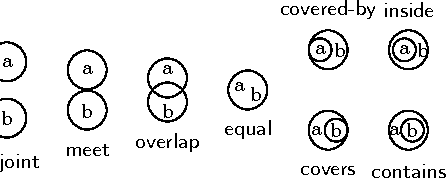
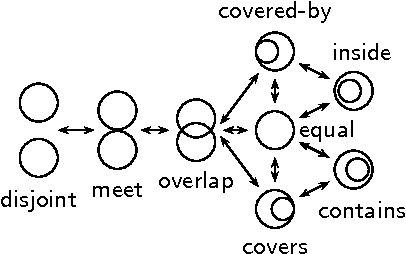
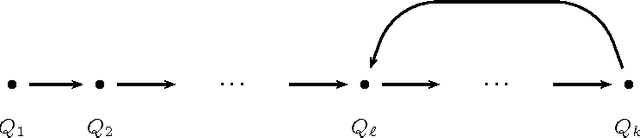
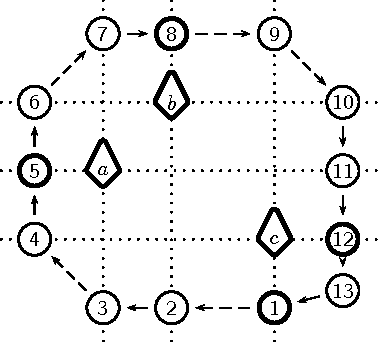
We introduce a constraint-based framework for studying infinite qualitative simulations concerned with contingencies such as time, space, shape, size, abstracted into a finite set of qualitative relations. To define the simulations, we combine constraints that formalize the background knowledge concerned with qualitative reasoning with appropriate inter-state constraints that are formulated using linear temporal logic. We implemented this approach in a constraint programming system by drawing on ideas from bounded model checking. The resulting system allows us to test and modify the problem specifications in a straightforward way and to combine various knowledge aspects.

Explaining Constraint Programming

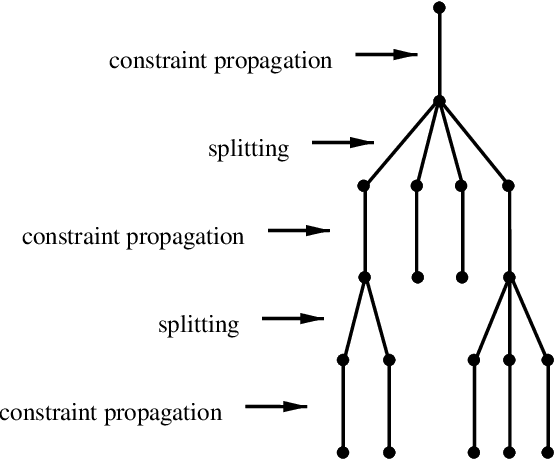
We discuss here constraint programming (CP) by using a proof-theoretic perspective. To this end we identify three levels of abstraction. Each level sheds light on the essence of CP. In particular, the highest level allows us to bring CP closer to the computation as deduction paradigm. At the middle level we can explain various constraint propagation algorithms. Finally, at the lowest level we can address the issue of automatic generation and optimization of the constraint propagation algorithms.

CP-nets and Nash equilibria

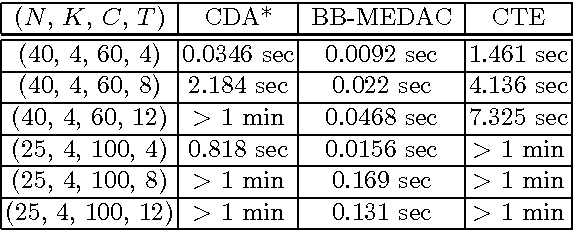
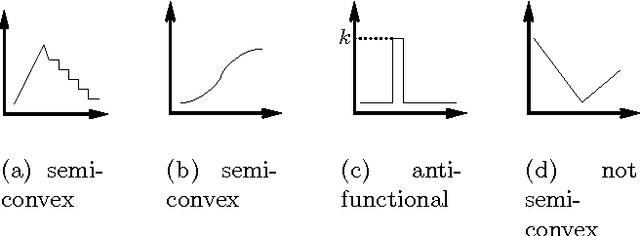
We relate here two formalisms that are used for different purposes in reasoning about multi-agent systems. One of them are strategic games that are used to capture the idea that agents interact with each other while pursuing their own interest. The other are CP-nets that were introduced to express qualitative and conditional preferences of the users and which aim at facilitating the process of preference elicitation. To relate these two formalisms we introduce a natural, qualitative, extension of the notion of a strategic game. We show then that the optimal outcomes of a CP-net are exactly the Nash equilibria of an appropriately defined strategic game in the above sense. This allows us to use the techniques of game theory to search for optimal outcomes of CP-nets and vice-versa, to use techniques developed for CP-nets to search for Nash equilibria of the considered games.