A Note on Nesting in Dyadic Deontic Logic

The paper reports on some results concerning Aqvist's dyadic logic known as system G, which is one of the most influential logics for reasoning with dyadic obligations ("it ought to be the case that ... if it is the case that ..."). Although this logic has been known in the literature for a while, many of its properties still await in-depth consideration. In this short paper we show: that any formula in system G including nested modal operators is equivalent to some formula with no nesting; that the universal modality introduced by Aqvist in the first presentation of the system is definable in terms of the deontic modality.

A Logic for Global and Local Announcements

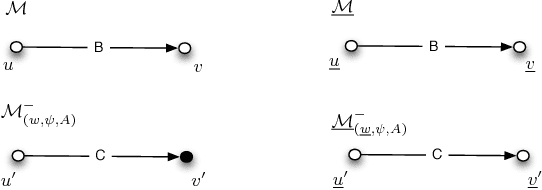
In this paper we introduce {\em global and local announcement logic} (GLAL), a dynamic epistemic logic with two distinct announcement operators -- $[\phi]^+_A$ and $[\phi]^-_A$ indexed to a subset $A$ of the set $Ag$ of all agents -- for global and local announcements respectively. The boundary case $[\phi]^+_{Ag}$ corresponds to the public announcement of $\phi$, as known from the literature. Unlike standard public announcements, which are {\em model transformers}, the global and local announcements are {\em pointed model transformers}. In particular, the update induced by the announcement may be different in different states of the model. Therefore, the resulting computations are trees of models, rather than the typical sequences. A consequence of our semantics is that modally bisimilar states may be distinguished in our logic. Then, we provide a stronger notion of bisimilarity and we show that it preserves modal equivalence in GLAL. Additionally, we show that GLAL is strictly more expressive than public announcement logic with common knowledge. We prove a wide range of validities for GLAL involving the interaction between dynamics and knowledge, and show that the satisfiability problem for GLAL is decidable. We illustrate the formal machinery by means of detailed epistemic scenarios.

Epistemic Protocols for Distributed Gossiping

Gossip protocols aim at arriving, by means of point-to-point or group communications, at a situation in which all the agents know each other's secrets. We consider distributed gossip protocols which are expressed by means of epistemic logic. We provide an operational semantics of such protocols and set up an appropriate framework to argue about their correctness. Then we analyze specific protocols for complete graphs and for directed rings.

An Introduction to Logics of Knowledge and Belief

This chapter provides an introduction to some basic concepts of epistemic logic, basic formal languages, their semantics, and proof systems. It also contains an overview of the handbook, and a brief history of epistemic logic and pointers to the literature.

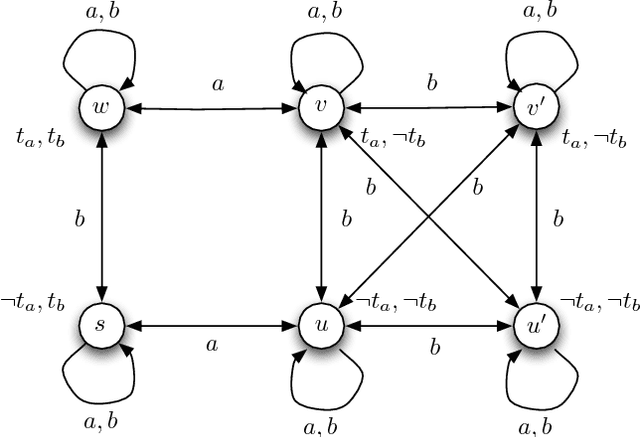
Reasoning About the Transfer of Control

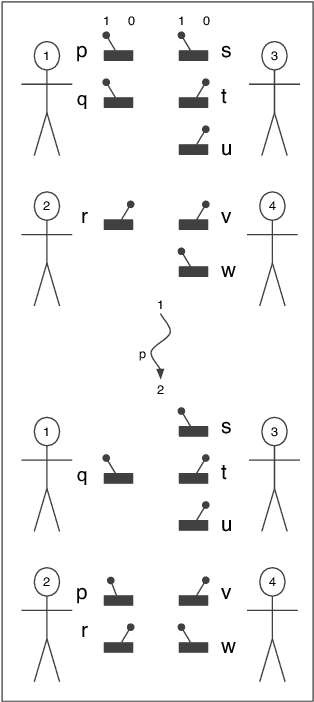
We present DCL-PC: a logic for reasoning about how the abilities of agents and coalitions of agents are altered by transferring control from one agent to another. The logical foundation of DCL-PC is CL-PC, a logic for reasoning about cooperation in which the abilities of agents and coalitions of agents stem from a distribution of atomic Boolean variables to individual agents -- the choices available to a coalition correspond to assignments to the variables the coalition controls. The basic modal constructs of DCL-PC are of the form coalition C can cooperate to bring about phi. DCL-PC extends CL-PC with dynamic logic modalities in which atomic programs are of the form agent i gives control of variable p to agent j; as usual in dynamic logic, these atomic programs may be combined using sequence, iteration, choice, and test operators to form complex programs. By combining such dynamic transfer programs with cooperation modalities, it becomes possible to reason about how the power of agents and coalitions is affected by the transfer of control. We give two alternative semantics for the logic: a direct semantics, in which we capture the distributions of Boolean variables to agents; and a more conventional Kripke semantics. We prove that these semantics are equivalent, and then present an axiomatization for the logic. We investigate the computational complexity of model checking and satisfiability for DCL-PC, and show that both problems are PSPACE-complete (and hence no worse than the underlying logic CL-PC). Finally, we investigate the characterisation of control in DCL-PC. We distinguish between first-order control -- the ability of an agent or coalition to control some state of affairs through the assignment of values to the variables under the control of the agent or coalition -- and second-order control -- the ability of an agent to exert control over the control that other agents have by transferring variables to other agents. We give a logical characterisation of second-order control.