Detecting Suspicious Events in Fast Information Flows

We describe a computational feather-light and intuitive, yet provably efficient algorithm, named HALFADO. HALFADO is designed for detecting suspicious events in a high-frequency stream of complex entries, based on a relatively small number of examples of human judgement. Operating a sufficiently accurate detection system is vital for {\em assisting} teams of human experts in many different areas of the modern digital society. These systems have intrinsically a far-reaching normative effect, and public knowledge of the workings of such technology should be a human right. On a conceptual level, the present approach extends one of the most classical learning algorithms for classification, inheriting its theoretical properties. It however works in a semi-supervised way integrating human and computational intelligence. On a practical level, this algorithm transcends existing approaches (expert systems) by managing and boosting their performance into a single global detector. We illustrate HALFADO's efficacy on two challenging applications: (1) for detecting {\em hate speech} messages in a flow of text messages gathered from a social media platform, and (2) for a Transaction Monitoring System (TMS) in FinTech detecting fraudulent transactions in a stream of financial transactions. This algorithm illustrates that - contrary to popular belief - advanced methods of machine learning need not require neither advanced levels of computation power nor expensive annotation efforts.

Longitudinal Support Vector Machines for High Dimensional Time Series

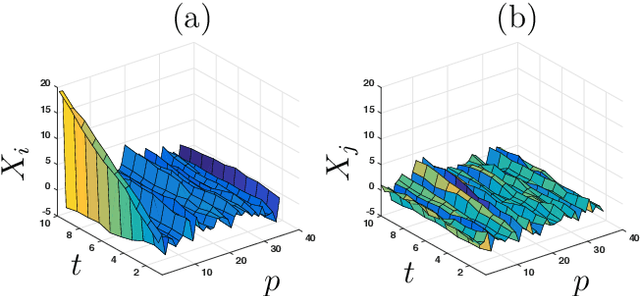
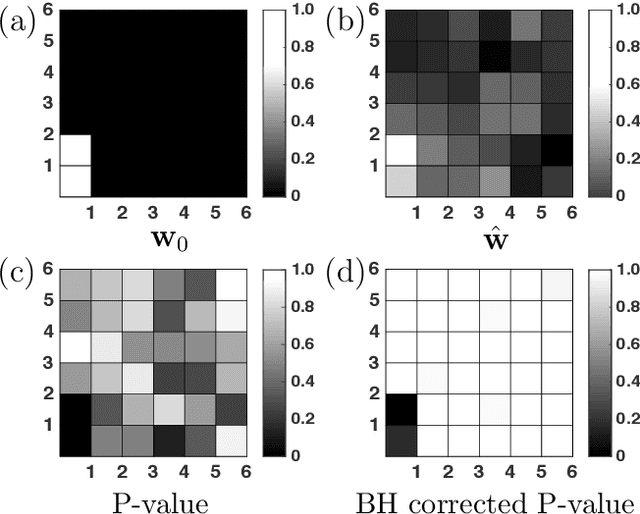
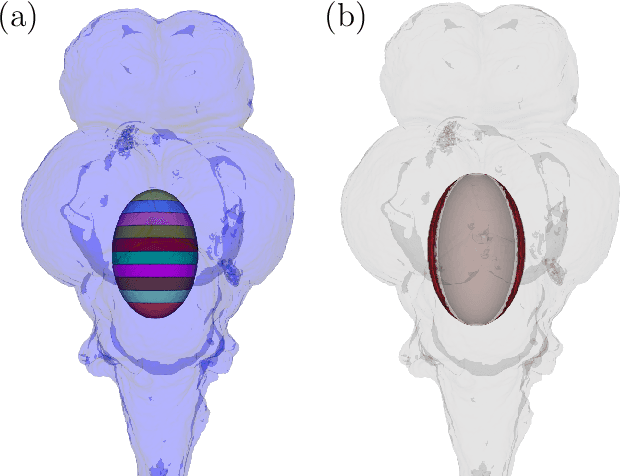
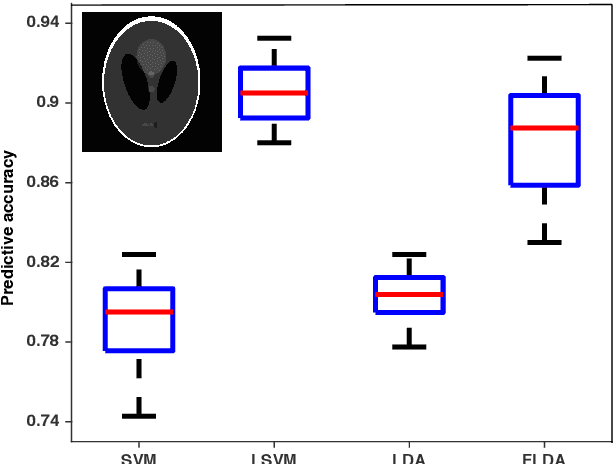
We consider the problem of learning a classifier from observed functional data. Here, each data-point takes the form of a single time-series and contains numerous features. Assuming that each such series comes with a binary label, the problem of learning to predict the label of a new coming time-series is considered. Hereto, the notion of {\em margin} underlying the classical support vector machine is extended to the continuous version for such data. The longitudinal support vector machine is also a convex optimization problem and its dual form is derived as well. Empirical results for specified cases with significance tests indicate the efficacy of this innovative algorithm for analyzing such long-term multivariate data.

APTER: Aggregated Prognosis Through Exponential Reweighting

This paper considers the task of learning how to make a prognosis of a patient based on his/her micro-array expression levels. The method is an application of the aggregation method as recently proposed in the literature on theoretical machine learning, and excels in its computational convenience and capability to deal with high-dimensional data. A formal analysis of the method is given, yielding rates of convergence similar to what traditional techniques obtain, while it is shown to cope well with an exponentially large set of features. Those results are supported by numerical simulations on a range of publicly available survival-micro-array datasets. It is empirically found that the proposed technique combined with a recently proposed preprocessing technique gives excellent performances.

FADO: A Deterministic Detection/Learning Algorithm

This paper proposes and studies a detection technique for adversarial scenarios (dubbed deterministic detection). This technique provides an alternative detection methodology in case the usual stochastic methods are not applicable: this can be because the studied phenomenon does not follow a stochastic sampling scheme, samples are high-dimensional and subsequent multiple-testing corrections render results overly conservative, sample sizes are too low for asymptotic results (as e.g. the central limit theorem) to kick in, or one cannot allow for the small probability of failure inherent to stochastic approaches. This paper instead designs a method based on insights from machine learning and online learning theory: this detection algorithm - named Online FAult Detection (FADO) - comes with theoretical guarantees of its detection capabilities. A version of the margin is found to regulate the detection performance of FADO. A precise expression is derived for bounding the performance, and experimental results are presented assessing the influence of involved quantities. A case study of scene detection is used to illustrate the approach. The technology is closely related to the linear perceptron rule, inherits its computational attractiveness and flexibility towards various extensions.

Sparse Estimation From Noisy Observations of an Overdetermined Linear System

This note studies a method for the efficient estimation of a finite number of unknown parameters from linear equations, which are perturbed by Gaussian noise. In case the unknown parameters have only few nonzero entries, the proposed estimator performs more efficiently than a traditional approach. The method consists of three steps: (1) a classical Least Squares Estimate (LSE), (2) the support is recovered through a Linear Programming (LP) optimization problem which can be computed using a soft-thresholding step, (3) a de-biasing step using a LSE on the estimated support set. The main contribution of this note is a formal derivation of an associated ORACLE property of the final estimate. That is, when the number of samples is large enough, the estimate is shown to equal the LSE based on the support of the {\em true} parameters.

MINLIP for the Identification of Monotone Wiener Systems

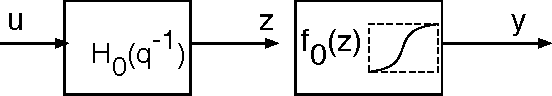
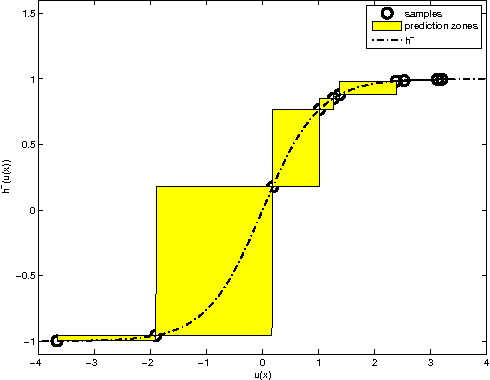
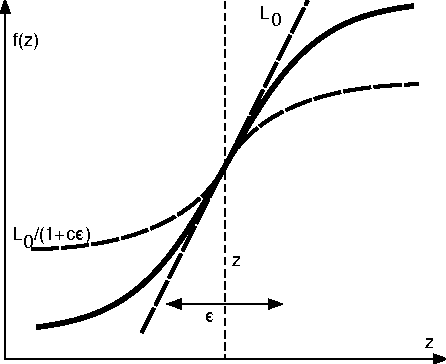
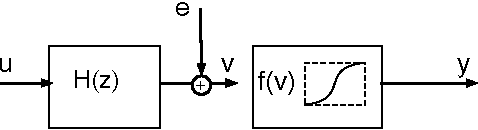
This paper studies the MINLIP estimator for the identification of Wiener systems consisting of a sequence of a linear FIR dynamical model, and a monotonically increasing (or decreasing) static function. Given $T$ observations, this algorithm boils down to solving a convex quadratic program with $O(T)$ variables and inequality constraints, implementing an inference technique which is based entirely on model complexity control. The resulting estimates of the linear submodel are found to be almost consistent when no noise is present in the data, under a condition of smoothness of the true nonlinearity and local Persistency of Excitation (local PE) of the data. This result is novel as it does not rely on classical tools as a 'linearization' using a Taylor decomposition, nor exploits stochastic properties of the data. It is indicated how to extend the method to cope with noisy data, and empirical evidence contrasts performance of the estimator against other recently proposed techniques.

Support and Quantile Tubes

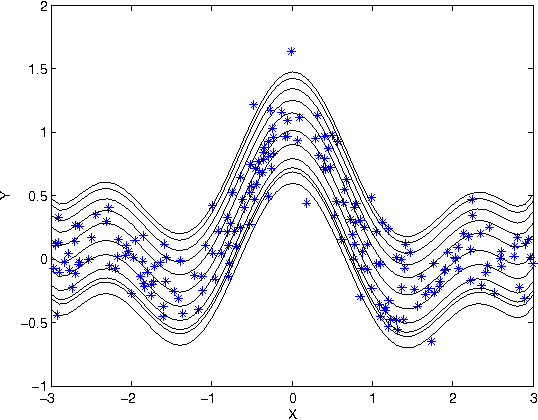
This correspondence studies an estimator of the conditional support of a distribution underlying a set of i.i.d. observations. The relation with mutual information is shown via an extension of Fano's theorem in combination with a generalization bound based on a compression argument. Extensions to estimating the conditional quantile interval, and statistical guarantees on the minimal convex hull are given.

Componentwise Least Squares Support Vector Machines

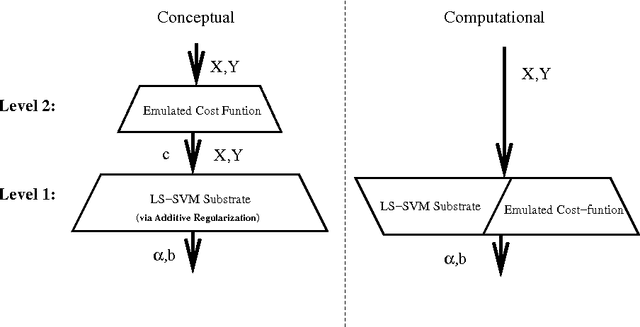
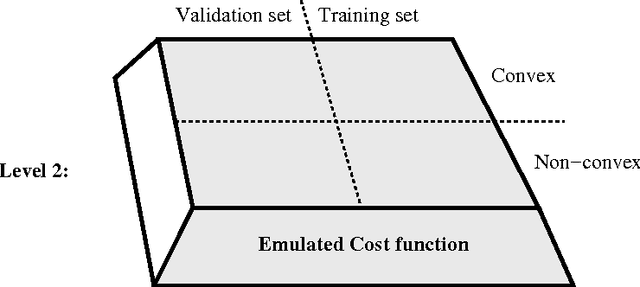
This chapter describes componentwise Least Squares Support Vector Machines (LS-SVMs) for the estimation of additive models consisting of a sum of nonlinear components. The primal-dual derivations characterizing LS-SVMs for the estimation of the additive model result in a single set of linear equations with size growing in the number of data-points. The derivation is elaborated for the classification as well as the regression case. Furthermore, different techniques are proposed to discover structure in the data by looking for sparse components in the model based on dedicated regularization schemes on the one hand and fusion of the componentwise LS-SVMs training with a validation criterion on the other hand. (keywords: LS-SVMs, additive models, regularization, structure detection)