MINLIP for the Identification of Monotone Wiener Systems
Paper and Code
Jun 24, 2010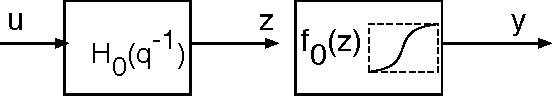
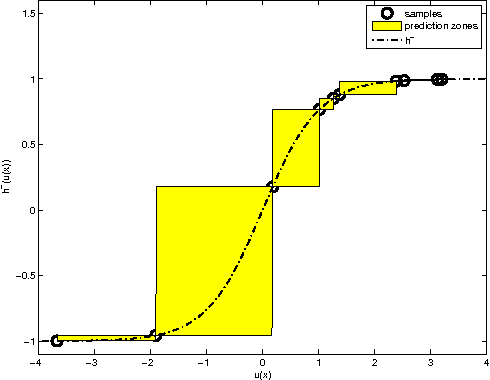
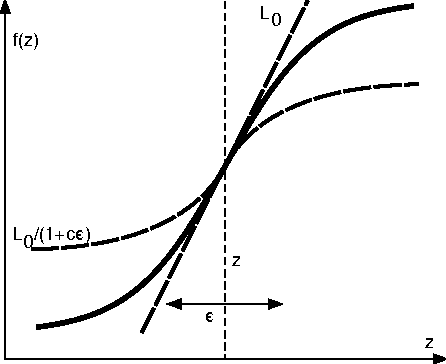
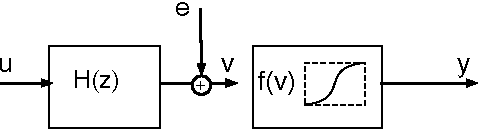
This paper studies the MINLIP estimator for the identification of Wiener systems consisting of a sequence of a linear FIR dynamical model, and a monotonically increasing (or decreasing) static function. Given $T$ observations, this algorithm boils down to solving a convex quadratic program with $O(T)$ variables and inequality constraints, implementing an inference technique which is based entirely on model complexity control. The resulting estimates of the linear submodel are found to be almost consistent when no noise is present in the data, under a condition of smoothness of the true nonlinearity and local Persistency of Excitation (local PE) of the data. This result is novel as it does not rely on classical tools as a 'linearization' using a Taylor decomposition, nor exploits stochastic properties of the data. It is indicated how to extend the method to cope with noisy data, and empirical evidence contrasts performance of the estimator against other recently proposed techniques.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge