Jos De Brabanter
Support and Quantile Tubes
Mar 12, 2007
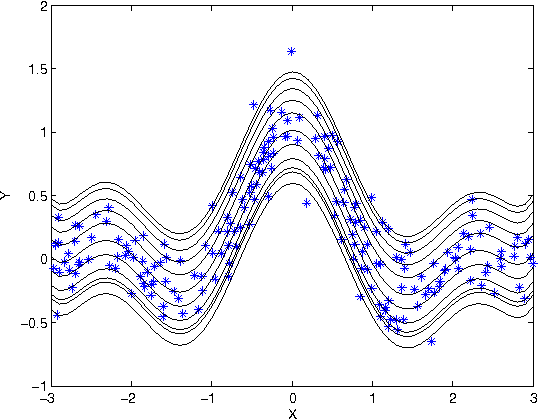
Abstract:This correspondence studies an estimator of the conditional support of a distribution underlying a set of i.i.d. observations. The relation with mutual information is shown via an extension of Fano's theorem in combination with a generalization bound based on a compression argument. Extensions to estimating the conditional quantile interval, and statistical guarantees on the minimal convex hull are given.
Componentwise Least Squares Support Vector Machines
Apr 19, 2005

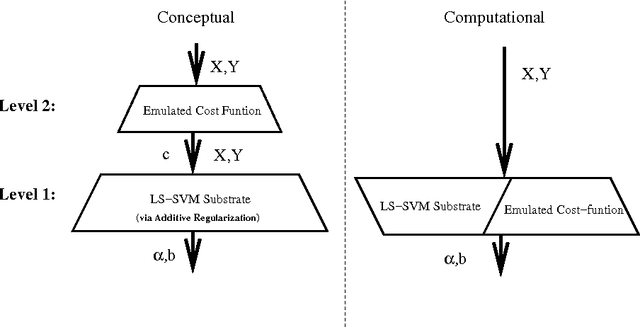
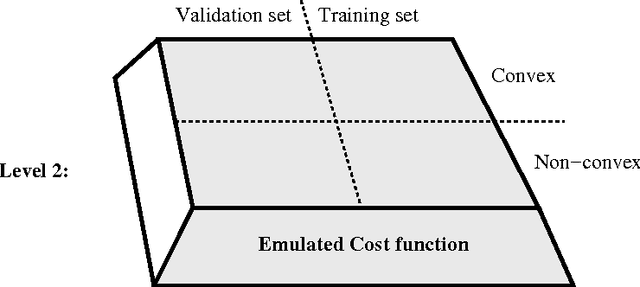
Abstract:This chapter describes componentwise Least Squares Support Vector Machines (LS-SVMs) for the estimation of additive models consisting of a sum of nonlinear components. The primal-dual derivations characterizing LS-SVMs for the estimation of the additive model result in a single set of linear equations with size growing in the number of data-points. The derivation is elaborated for the classification as well as the regression case. Furthermore, different techniques are proposed to discover structure in the data by looking for sparse components in the model based on dedicated regularization schemes on the one hand and fusion of the componentwise LS-SVMs training with a validation criterion on the other hand. (keywords: LS-SVMs, additive models, regularization, structure detection)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge