Optimal-State Dynamics Estimation for Physics-based Human Motion Capture from Videos

Human motion capture from monocular videos has made significant progress in recent years. However, modern approaches often produce temporal artifacts, e.g. in form of jittery motion and struggle to achieve smooth and physically plausible motions. Explicitly integrating physics, in form of internal forces and exterior torques, helps alleviating these artifacts. Current state-of-the-art approaches make use of an automatic PD controller to predict torques and reaction forces in order to re-simulate the input kinematics, i.e. the joint angles of a predefined skeleton. However, due to imperfect physical models, these methods often require simplifying assumptions and extensive preprocessing of the input kinematics to achieve good performance. To this end, we propose a novel method to selectively incorporate the physics models with the kinematics observations in an online setting, inspired by a neural Kalman-filtering approach. We develop a control loop as a meta-PD controller to predict internal joint torques and external reaction forces, followed by a physics-based motion simulation. A recurrent neural network is introduced to realize a Kalman filter that attentively balances the kinematics input and simulated motion, resulting in an optimal-state dynamics prediction. We show that this filtering step is crucial to provide an online supervision that helps balancing the shortcoming of the respective input motions, thus being important for not only capturing accurate global motion trajectories but also producing physically plausible human poses. The proposed approach excels in the physics-based human pose estimation task and demonstrates the physical plausibility of the predictive dynamics, compared to state of the art. The code is available on https://github.com/cuongle1206/OSDCap

Tensor network square root Kalman filter for online Gaussian process regression

The state-of-the-art tensor network Kalman filter lifts the curse of dimensionality for high-dimensional recursive estimation problems. However, the required rounding operation can cause filter divergence due to the loss of positive definiteness of covariance matrices. We solve this issue by developing, for the first time, a tensor network square root Kalman filter, and apply it to high-dimensional online Gaussian process regression. In our experiments, we demonstrate that our method is equivalent to the conventional Kalman filter when choosing a full-rank tensor network. Furthermore, we apply our method to a real-life system identification problem where we estimate $4^{14}$ parameters on a standard laptop. The estimated model outperforms the state-of-the-art tensor network Kalman filter in terms of prediction accuracy and uncertainty quantification.

Online One-Dimensional Magnetic Field SLAM with Loop-Closure Detection

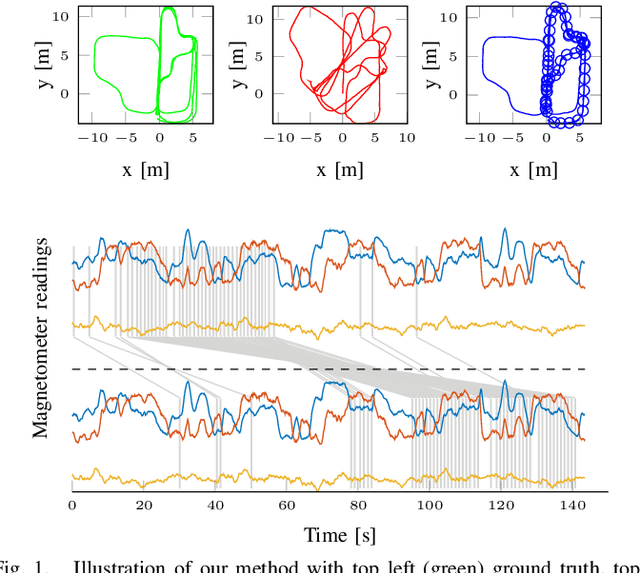
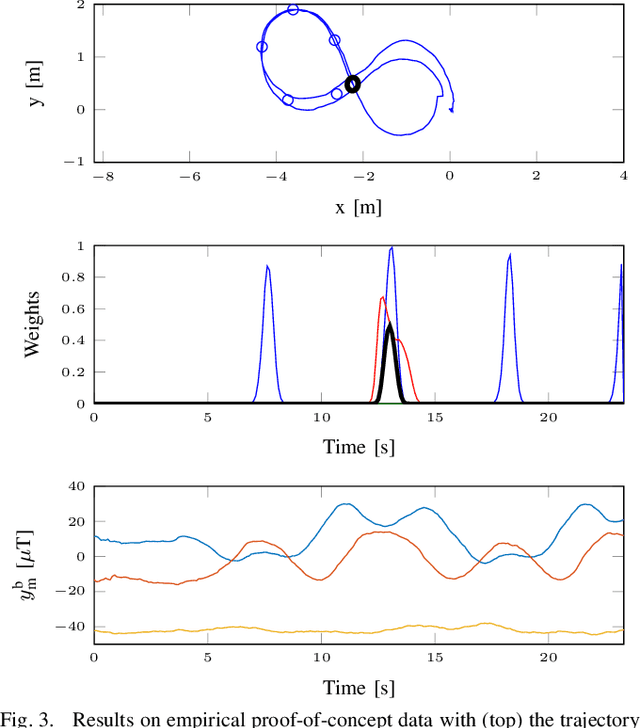
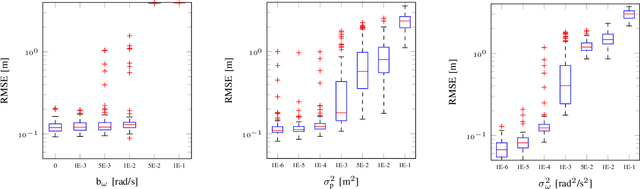
We present a lightweight magnetic field simultaneous localisation and mapping (SLAM) approach for drift correction in odometry paths, where the interest is purely in the odometry and not in map building. We represent the past magnetic field readings as a one-dimensional trajectory against which the current magnetic field observations are matched. This approach boils down to sequential loop-closure detection and decision-making, based on the current pose state estimate and the magnetic field. We combine this setup with a path estimation framework using an extended Kalman smoother which fuses the odometry increments with the detected loop-closure timings. We demonstrate the practical applicability of the model with several different real-world examples from a handheld iPad moving in indoor scenes.

Projecting basis functions with tensor networks for Gaussian process regression

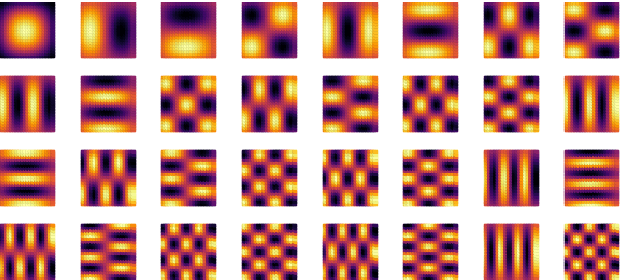
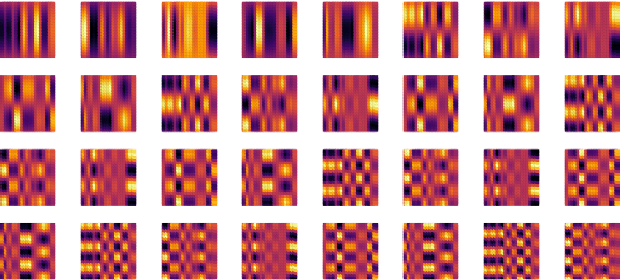
This paper presents a method for approximate Gaussian process (GP) regression with tensor networks (TNs). A parametric approximation of a GP uses a linear combination of basis functions, where the accuracy of the approximation depends on the total number of basis functions $M$. We develop an approach that allows us to use an exponential amount of basis functions without the corresponding exponential computational complexity. The key idea to enable this is using low-rank TNs. We first find a suitable low-dimensional subspace from the data, described by a low-rank TN. In this low-dimensional subspace, we then infer the weights of our model by solving a Bayesian inference problem. Finally, we project the resulting weights back to the original space to make GP predictions. The benefit of our approach comes from the projection to a smaller subspace: It modifies the shape of the basis functions in a way that it sees fit based on the given data, and it allows for efficient computations in the smaller subspace. In an experiment with an 18-dimensional benchmark data set, we show the applicability of our method to an inverse dynamics problem.

Distributed multi-agent magnetic field norm SLAM with Gaussian processes

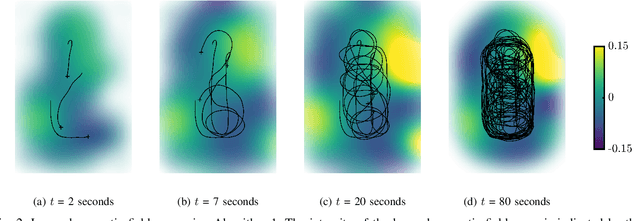
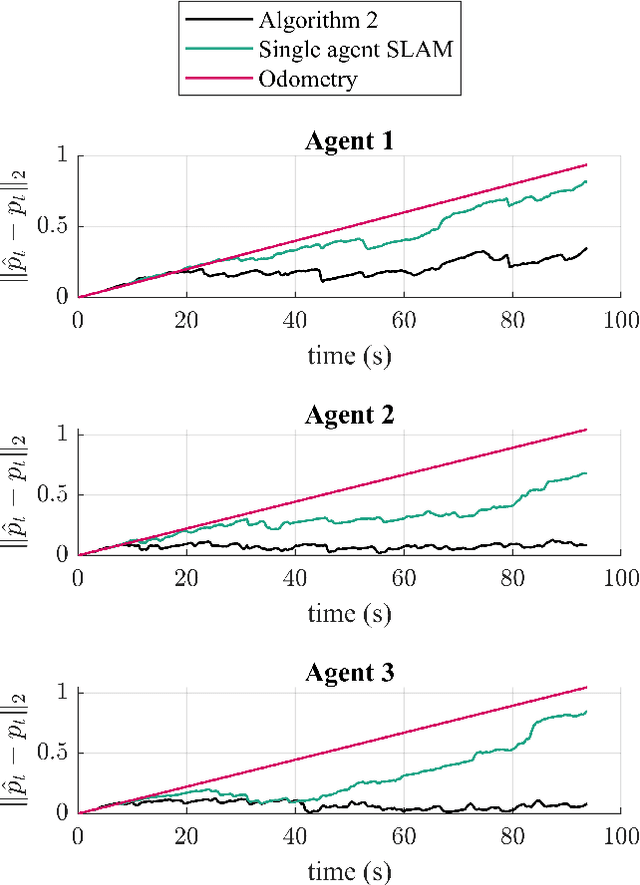
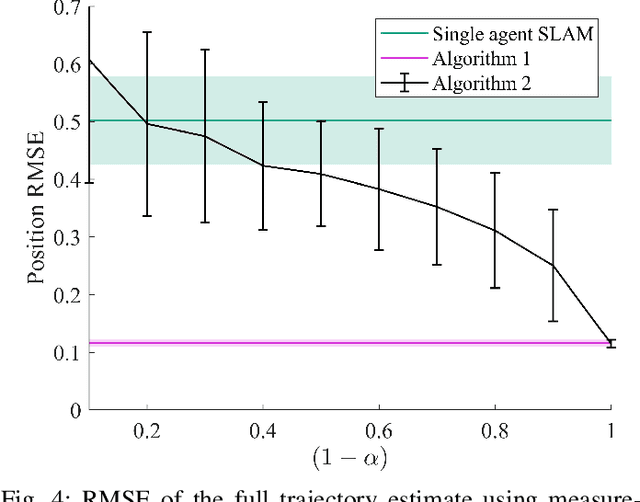
Accurately estimating the positions of multi-agent systems in indoor environments is challenging due to the lack of Global Navigation Satelite System (GNSS) signals. Noisy measurements of position and orientation can cause the integrated position estimate to drift without bound. Previous research has proposed using magnetic field simultaneous localization and mapping (SLAM) to compensate for position drift in a single agent. Here, we propose two novel algorithms that allow multiple agents to apply magnetic field SLAM using their own and other agents measurements. Our first algorithm is a centralized approach that uses all measurements collected by all agents in a single extended Kalman filter. This algorithm simultaneously estimates the agents position and orientation and the magnetic field norm in a central unit that can communicate with all agents at all times. In cases where a central unit is not available, and there are communication drop-outs between agents, our second algorithm is a distributed approach that can be employed. We tested both algorithms by estimating the position of magnetometers carried by three people in an optical motion capture lab with simulated odometry and simulated communication dropouts between agents. We show that both algorithms are able to compensate for drift in a case where single-agent SLAM is not. We also discuss the conditions for the estimate from our distributed algorithm to converge to the estimate from the centralized algorithm, both theoretically and experimentally. Our experiments show that, for a communication drop-out rate of 80 percent, our proposed distributed algorithm, on average, provides a more accurate position estimate than single-agent SLAM. Finally, we demonstrate the drift-compensating abilities of our centralized algorithm on a real-life pedestrian localization problem with multiple agents moving inside a building.

Large-scale magnetic field maps using structured kernel interpolation for Gaussian process regression

We present a mapping algorithm to compute large-scale magnetic field maps in indoor environments with approximate Gaussian process (GP) regression. Mapping the spatial variations in the ambient magnetic field can be used for localization algorithms in indoor areas. To compute such a map, GP regression is a suitable tool because it provides predictions of the magnetic field at new locations along with uncertainty quantification. Because full GP regression has a complexity that grows cubically with the number of data points, approximations for GPs have been extensively studied. In this paper, we build on the structured kernel interpolation (SKI) framework, speeding up inference by exploiting efficient Krylov subspace methods. More specifically, we incorporate SKI with derivatives (D-SKI) into the scalar potential model for magnetic field modeling and compute both predictive mean and covariance with a complexity that is linear in the data points. In our simulations, we show that our method achieves better accuracy than current state-of-the-art methods on magnetic field maps with a growing mapping area. In our large-scale experiments, we construct magnetic field maps from up to 40000 three-dimensional magnetic field measurements in less than two minutes on a standard laptop.

Mapping the magnetic field using a magnetometer array with noisy input Gaussian process regression

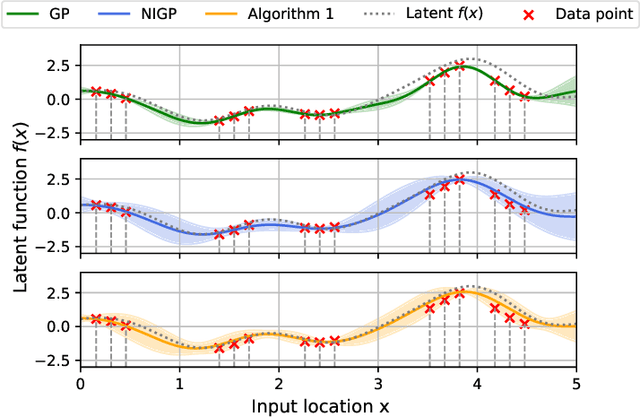
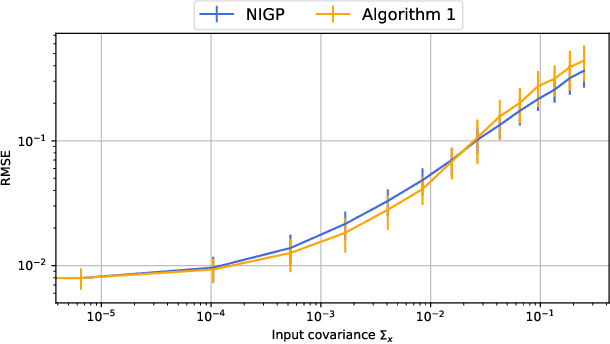
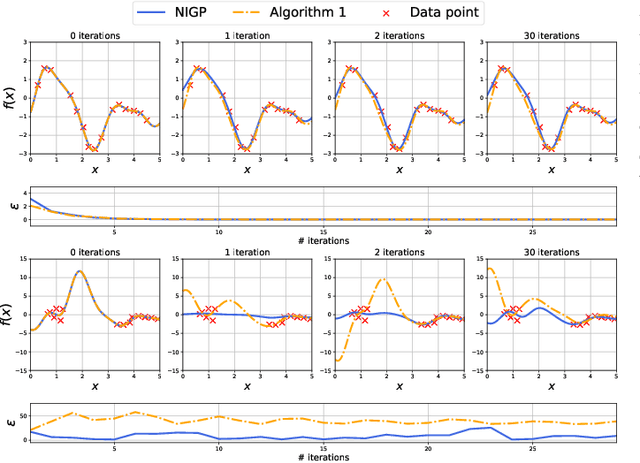
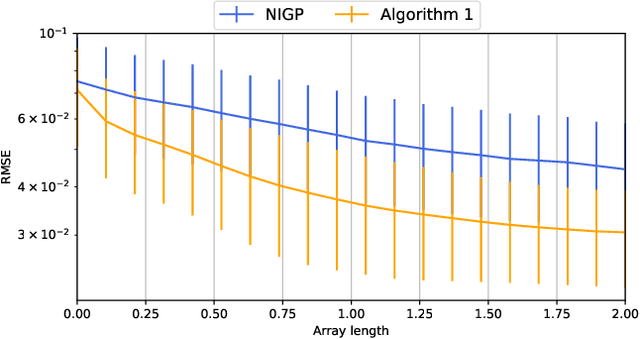
Ferromagnetic materials in indoor environments give rise to disturbances in the ambient magnetic field. Maps of these magnetic disturbances can be used for indoor localisation. A Gaussian process can be used to learn the spatially varying magnitude of the magnetic field using magnetometer measurements and information about the position of the magnetometer. The position of the magnetometer, however, is frequently only approximately known. This negatively affects the quality of the magnetic field map. In this paper, we investigate how an array of magnetometers can be used to improve the quality of the magnetic field map. The position of the array is approximately known, but the relative locations of the magnetometers on the array are known. We include this information in a novel method to make a map of the ambient magnetic field. We study the properties of our method in simulation and show that our method improves the map quality. We also demonstrate the efficacy of our method with experimental data for the mapping of the magnetic field using an array of 30 magnetometers.

Rao-Blackwellized Particle Smoothing for Simultaneous Localization and Mapping

Simultaneous localization and mapping (SLAM) is the task of building a map representation of an unknown environment while it at the same time is used for positioning. A probabilistic interpretation of the SLAM task allows for incorporating prior knowledge and for operation under uncertainty. Contrary to the common practice of computing point estimates of the system states, we capture the full posterior density through approximate Bayesian inference. This dynamic learning task falls under state estimation, where the state-of-the-art is in sequential Monte Carlo methods that tackle the forward filtering problem. In this paper, we introduce a framework for probabilistic SLAM using particle smoothing that does not only incorporate observed data in current state estimates, but it also back-tracks the updated knowledge to correct for past drift and ambiguities in both the map and in the states. Our solution can efficiently handle both dense and sparse map representations by Rao-Blackwellization of conditionally linear and conditionally linearized models. We show through simulations and real-world experiments how the principles apply to radio (BLE/Wi-Fi), magnetic field, and visual SLAM. The proposed solution is general, efficient, and works well under confounding noise.

Tightly Integrated Motion Classification and State Estimation in Foot-Mounted Navigation Systems

A framework for tightly integrated motion mode classification and state estimation in motion-constrained inertial navigation systems is presented. The framework uses a jump Markov model to describe the navigation system's motion mode and navigation state dynamics with a single model. A bank of Kalman filters is then used for joint inference of the navigation state and the motion mode. A method for learning unknown parameters in the jump Markov model, such as the motion mode transition probabilities, is also presented. The application of the proposed framework is illustrated via two examples. The first example is a foot-mounted navigation system that adapts its behavior to different gait speeds. The second example is a foot-mounted navigation system that detects when the user walks on flat ground and locks the vertical position estimate accordingly. Both examples show that the proposed framework provides significantly better position accuracy than a standard zero-velocity aided inertial navigation system. More importantly, the examples show that the proposed framework provides a theoretically well-grounded approach for developing new motion-constrained inertial navigation systems that can learn different motion patterns.

Fast Gaussian Process Predictions on Large Geospatial Fields with Prediction-Point Dependent Basis Functions

In order to perform GP predictions fast in large geospatial fields with small-scale variations, a computational complexity that is independent of the number of measurements $N$ and the size of the field is crucial. In this setting, GP approximations using $m$ basis functions requires $\mathcal{O}(Nm^2+m^3)$ computations. Using finite-support basis functions reduces the required number of computations to perform a single prediction to $\mathcal{O}(m^3)$, after a one-time training cost of $O(N)$. The prediction cost increases with increasing field size, as the number of required basis functions $m$ grows with the size of the field relative to the size of the spatial variations. To prevent the prediction speed from depending on field size, we propose leveraging the property that a subset of the trained system is a trained subset of the system to use only a local subset of $m'\ll m$ finite-support basis functions centered around each prediction point to perform predictions. Our proposed approximation requires $\mathcal{O}(m'^3)$ operations to perform each prediction after a one-time training cost of $\mathcal{O}(N)$. We show on real-life spatial data that our approach matches the prediction error of state-of-the-art methods and that it performs faster predictions, also compared to state-of-the-art approximations that lower the prediction cost of $\mathcal{O}(m^3)$ to $\mathcal{O}(m\log(m))$ using a conjugate gradient solver. Finally, we demonstrate that our approach can perform fast predictions on a global bathymetry dataset using millions of basis functions and tens of millions of measurements on a laptop computer.