Projecting basis functions with tensor networks for Gaussian process regression

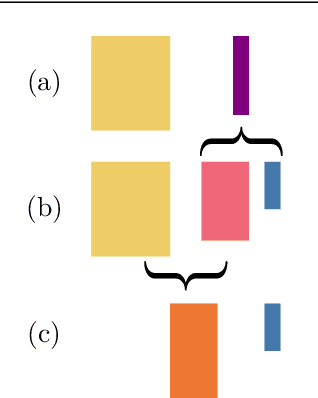
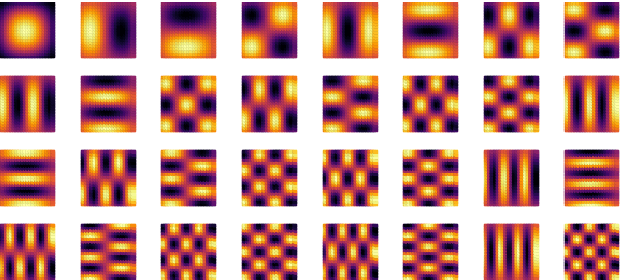
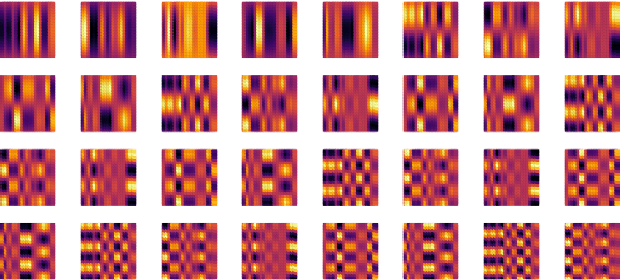
This paper presents a method for approximate Gaussian process (GP) regression with tensor networks (TNs). A parametric approximation of a GP uses a linear combination of basis functions, where the accuracy of the approximation depends on the total number of basis functions $M$. We develop an approach that allows us to use an exponential amount of basis functions without the corresponding exponential computational complexity. The key idea to enable this is using low-rank TNs. We first find a suitable low-dimensional subspace from the data, described by a low-rank TN. In this low-dimensional subspace, we then infer the weights of our model by solving a Bayesian inference problem. Finally, we project the resulting weights back to the original space to make GP predictions. The benefit of our approach comes from the projection to a smaller subspace: It modifies the shape of the basis functions in a way that it sees fit based on the given data, and it allows for efficient computations in the smaller subspace. In an experiment with an 18-dimensional benchmark data set, we show the applicability of our method to an inverse dynamics problem.

Towards Green AI with tensor networks -- Sustainability and innovation enabled by efficient algorithms

The current standard to compare the performance of AI algorithms is mainly based on one criterion: the model's accuracy. In this context, algorithms with a higher accuracy (or similar measures) are considered as better. To achieve new state-of-the-art results, algorithmic development is accompanied by an exponentially increasing amount of compute. While this has enabled AI research to achieve remarkable results, AI progress comes at a cost: it is unsustainable. In this paper, we present a promising tool for sustainable and thus Green AI: tensor networks (TNs). Being an established tool from multilinear algebra, TNs have the capability to improve efficiency without compromising accuracy. Since they can reduce compute significantly, we would like to highlight their potential for Green AI. We elaborate in both a kernel machine and deep learning setting how efficiency gains can be achieved with TNs. Furthermore, we argue that better algorithms should be evaluated in terms of both accuracy and efficiency. To that end, we discuss different efficiency criteria and analyze efficiency in an exemplifying experimental setting for kernel ridge regression. With this paper, we want to raise awareness about Green AI and showcase its positive impact on sustainability and AI research. Our key contribution is to demonstrate that TNs enable efficient algorithms and therefore contribute towards Green AI. In this sense, TNs pave the way for better algorithms in AI.