Tensor network square root Kalman filter for online Gaussian process regression

The state-of-the-art tensor network Kalman filter lifts the curse of dimensionality for high-dimensional recursive estimation problems. However, the required rounding operation can cause filter divergence due to the loss of positive definiteness of covariance matrices. We solve this issue by developing, for the first time, a tensor network square root Kalman filter, and apply it to high-dimensional online Gaussian process regression. In our experiments, we demonstrate that our method is equivalent to the conventional Kalman filter when choosing a full-rank tensor network. Furthermore, we apply our method to a real-life system identification problem where we estimate $4^{14}$ parameters on a standard laptop. The estimated model outperforms the state-of-the-art tensor network Kalman filter in terms of prediction accuracy and uncertainty quantification.

Projecting basis functions with tensor networks for Gaussian process regression

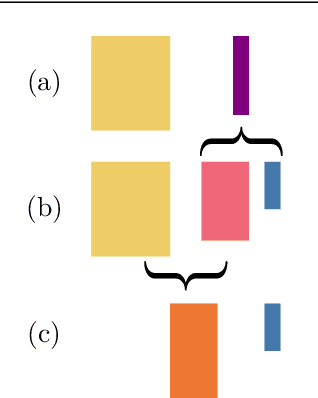
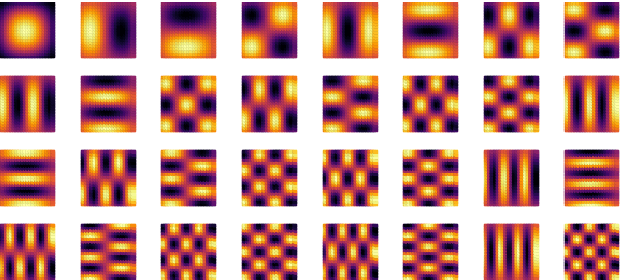
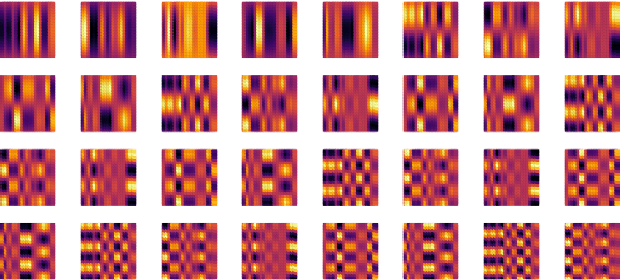
This paper presents a method for approximate Gaussian process (GP) regression with tensor networks (TNs). A parametric approximation of a GP uses a linear combination of basis functions, where the accuracy of the approximation depends on the total number of basis functions $M$. We develop an approach that allows us to use an exponential amount of basis functions without the corresponding exponential computational complexity. The key idea to enable this is using low-rank TNs. We first find a suitable low-dimensional subspace from the data, described by a low-rank TN. In this low-dimensional subspace, we then infer the weights of our model by solving a Bayesian inference problem. Finally, we project the resulting weights back to the original space to make GP predictions. The benefit of our approach comes from the projection to a smaller subspace: It modifies the shape of the basis functions in a way that it sees fit based on the given data, and it allows for efficient computations in the smaller subspace. In an experiment with an 18-dimensional benchmark data set, we show the applicability of our method to an inverse dynamics problem.

Large-scale magnetic field maps using structured kernel interpolation for Gaussian process regression

We present a mapping algorithm to compute large-scale magnetic field maps in indoor environments with approximate Gaussian process (GP) regression. Mapping the spatial variations in the ambient magnetic field can be used for localization algorithms in indoor areas. To compute such a map, GP regression is a suitable tool because it provides predictions of the magnetic field at new locations along with uncertainty quantification. Because full GP regression has a complexity that grows cubically with the number of data points, approximations for GPs have been extensively studied. In this paper, we build on the structured kernel interpolation (SKI) framework, speeding up inference by exploiting efficient Krylov subspace methods. More specifically, we incorporate SKI with derivatives (D-SKI) into the scalar potential model for magnetic field modeling and compute both predictive mean and covariance with a complexity that is linear in the data points. In our simulations, we show that our method achieves better accuracy than current state-of-the-art methods on magnetic field maps with a growing mapping area. In our large-scale experiments, we construct magnetic field maps from up to 40000 three-dimensional magnetic field measurements in less than two minutes on a standard laptop.

Towards Green AI with tensor networks -- Sustainability and innovation enabled by efficient algorithms

The current standard to compare the performance of AI algorithms is mainly based on one criterion: the model's accuracy. In this context, algorithms with a higher accuracy (or similar measures) are considered as better. To achieve new state-of-the-art results, algorithmic development is accompanied by an exponentially increasing amount of compute. While this has enabled AI research to achieve remarkable results, AI progress comes at a cost: it is unsustainable. In this paper, we present a promising tool for sustainable and thus Green AI: tensor networks (TNs). Being an established tool from multilinear algebra, TNs have the capability to improve efficiency without compromising accuracy. Since they can reduce compute significantly, we would like to highlight their potential for Green AI. We elaborate in both a kernel machine and deep learning setting how efficiency gains can be achieved with TNs. Furthermore, we argue that better algorithms should be evaluated in terms of both accuracy and efficiency. To that end, we discuss different efficiency criteria and analyze efficiency in an exemplifying experimental setting for kernel ridge regression. With this paper, we want to raise awareness about Green AI and showcase its positive impact on sustainability and AI research. Our key contribution is to demonstrate that TNs enable efficient algorithms and therefore contribute towards Green AI. In this sense, TNs pave the way for better algorithms in AI.

Alternating linear scheme in a Bayesian framework for low-rank tensor approximation

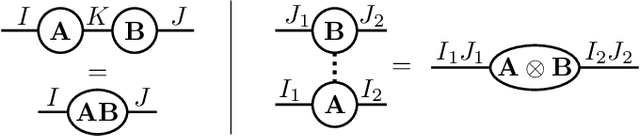
Multiway data often naturally occurs in a tensorial format which can be approximately represented by a low-rank tensor decomposition. This is useful because complexity can be significantly reduced and the treatment of large-scale data sets can be facilitated. In this paper, we find a low-rank representation for a given tensor by solving a Bayesian inference problem. This is achieved by dividing the overall inference problem into sub-problems where we sequentially infer the posterior distribution of one tensor decomposition component at a time. This leads to a probabilistic interpretation of the well-known iterative algorithm alternating linear scheme (ALS). In this way, the consideration of measurement noise is enabled, as well as the incorporation of application-specific prior knowledge and the uncertainty quantification of the low-rank tensor estimate. To compute the low-rank tensor estimate from the posterior distributions of the tensor decomposition components, we present an algorithm that performs the unscented transform in tensor train format.