A Kernelizable Primal-Dual Formulation of the Multilinear Singular Value Decomposition

The ability to express a learning task in terms of a primal and a dual optimization problem lies at the core of a plethora of machine learning methods. For example, Support Vector Machine (SVM), Least-Squares Support Vector Machine (LS-SVM), Ridge Regression (RR), Lasso Regression (LR), Principal Component Analysis (PCA), and more recently Singular Value Decomposition (SVD) have all been defined either in terms of primal weights or in terms of dual Lagrange multipliers. The primal formulation is computationally advantageous in the case of large sample size while the dual is preferred for high-dimensional data. Crucially, said learning problems can be made nonlinear through the introduction of a feature map in the primal problem, which corresponds to applying the kernel trick in the dual. In this paper we derive a primal-dual formulation of the Multilinear Singular Value Decomposition (MLSVD), which recovers as special cases both PCA and SVD. Besides enabling computational gains through the derived primal formulation, we propose a nonlinear extension of the MLSVD using feature maps, which results in a dual problem where a kernel tensor arises. We discuss potential applications in the context of signal analysis and deep learning.

Exploiting Hankel-Toeplitz Structures for Fast Computation of Kernel Precision Matrices

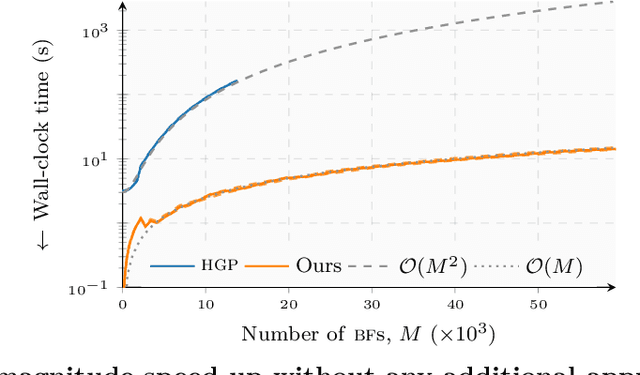
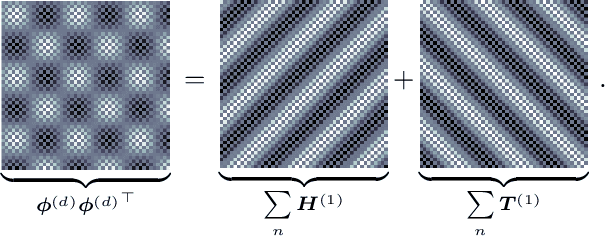
The Hilbert-space Gaussian Process (HGP) approach offers a hyperparameter-independent basis function approximation for speeding up Gaussian Process (GP) inference by projecting the GP onto M basis functions. These properties result in a favorable data-independent $\mathcal{O}(M^3)$ computational complexity during hyperparameter optimization but require a dominating one-time precomputation of the precision matrix costing $\mathcal{O}(NM^2)$ operations. In this paper, we lower this dominating computational complexity to $\mathcal{O}(NM)$ with no additional approximations. We can do this because we realize that the precision matrix can be split into a sum of Hankel-Toeplitz matrices, each having $\mathcal{O}(M)$ unique entries. Based on this realization we propose computing only these unique entries at $\mathcal{O}(NM)$ costs. Further, we develop two theorems that prescribe sufficient conditions for the complexity reduction to hold generally for a wide range of other approximate GP models, such as the Variational Fourier Feature (VFF) approach. The two theorems do this with no assumptions on the data and no additional approximations of the GP models themselves. Thus, our contribution provides a pure speed-up of several existing, widely used, GP approximations, without further approximations.

Efficient Patient Fine-Tuned Seizure Detection with a Tensor Kernel Machine

Recent developments in wearable devices have made accurate and efficient seizure detection more important than ever. A challenge in seizure detection is that patient-specific models typically outperform patient-independent models. However, in a wearable device one typically starts with a patient-independent model, until such patient-specific data is available. To avoid having to construct a new classifier with this data, as required in conventional kernel machines, we propose a transfer learning approach with a tensor kernel machine. This method learns the primal weights in a compressed form using the canonical polyadic decomposition, making it possible to efficiently update the weights of the patient-independent model with patient-specific data. The results show that this patient fine-tuned model reaches as high a performance as a patient-specific SVM model with a model size that is twice as small as the patient-specific model and ten times as small as the patient-independent model.

Tensor Network-Constrained Kernel Machines as Gaussian Processes

Tensor Networks (TNs) have recently been used to speed up kernel machines by constraining the model weights, yielding exponential computational and storage savings. In this paper we prove that the outputs of Canonical Polyadic Decomposition (CPD) and Tensor Train (TT)-constrained kernel machines recover a Gaussian Process (GP), which we fully characterize, when placing i.i.d. priors over their parameters. We analyze the convergence of both CPD and TT-constrained models, and show how TT yields models exhibiting more GP behavior compared to CPD, for the same number of model parameters. We empirically observe this behavior in two numerical experiments where we respectively analyze the convergence to the GP and the performance at prediction. We thereby establish a connection between TN-constrained kernel machines and GPs.

Quantized Fourier and Polynomial Features for more Expressive Tensor Network Models

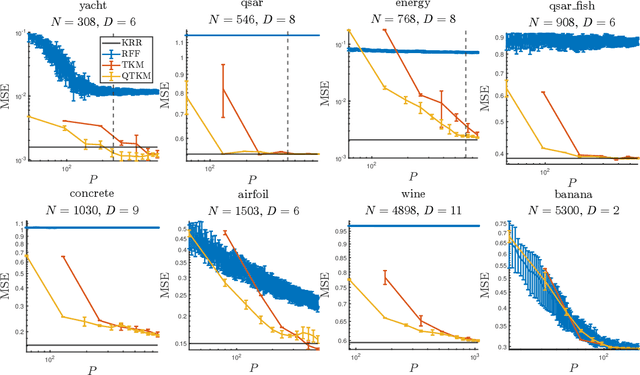
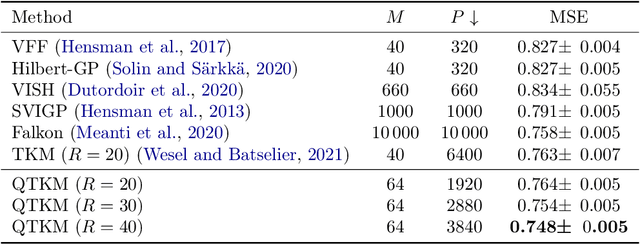
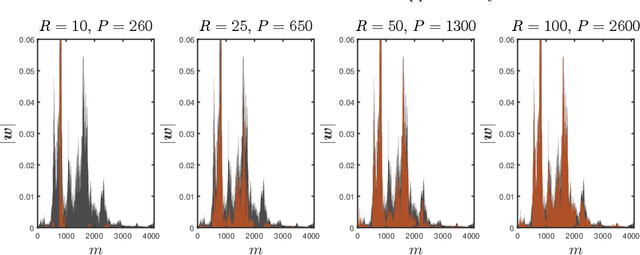
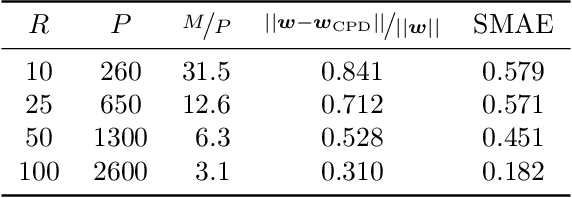
In the context of kernel machines, polynomial and Fourier features are commonly used to provide a nonlinear extension to linear models by mapping the data to a higher-dimensional space. Unless one considers the dual formulation of the learning problem, which renders exact large-scale learning unfeasible, the exponential increase of model parameters in the dimensionality of the data caused by their tensor-product structure prohibits to tackle high-dimensional problems. One of the possible approaches to circumvent this exponential scaling is to exploit the tensor structure present in the features by constraining the model weights to be an underparametrized tensor network. In this paper we quantize, i.e. further tensorize, polynomial and Fourier features. Based on this feature quantization we propose to quantize the associated model weights, yielding quantized models. We show that, for the same number of model parameters, the resulting quantized models have a higher bound on the VC-dimension as opposed to their non-quantized counterparts, at no additional computational cost while learning from identical features. We verify experimentally how this additional tensorization regularizes the learning problem by prioritizing the most salient features in the data and how it provides models with increased generalization capabilities. We finally benchmark our approach on large regression task, achieving state-of-the-art results on a laptop computer.

Towards Green AI with tensor networks -- Sustainability and innovation enabled by efficient algorithms

The current standard to compare the performance of AI algorithms is mainly based on one criterion: the model's accuracy. In this context, algorithms with a higher accuracy (or similar measures) are considered as better. To achieve new state-of-the-art results, algorithmic development is accompanied by an exponentially increasing amount of compute. While this has enabled AI research to achieve remarkable results, AI progress comes at a cost: it is unsustainable. In this paper, we present a promising tool for sustainable and thus Green AI: tensor networks (TNs). Being an established tool from multilinear algebra, TNs have the capability to improve efficiency without compromising accuracy. Since they can reduce compute significantly, we would like to highlight their potential for Green AI. We elaborate in both a kernel machine and deep learning setting how efficiency gains can be achieved with TNs. Furthermore, we argue that better algorithms should be evaluated in terms of both accuracy and efficiency. To that end, we discuss different efficiency criteria and analyze efficiency in an exemplifying experimental setting for kernel ridge regression. With this paper, we want to raise awareness about Green AI and showcase its positive impact on sustainability and AI research. Our key contribution is to demonstrate that TNs enable efficient algorithms and therefore contribute towards Green AI. In this sense, TNs pave the way for better algorithms in AI.

Large-Scale Learning with Fourier Features and Tensor Decompositions

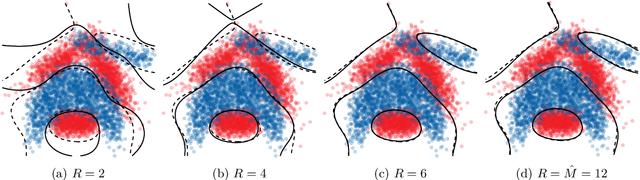
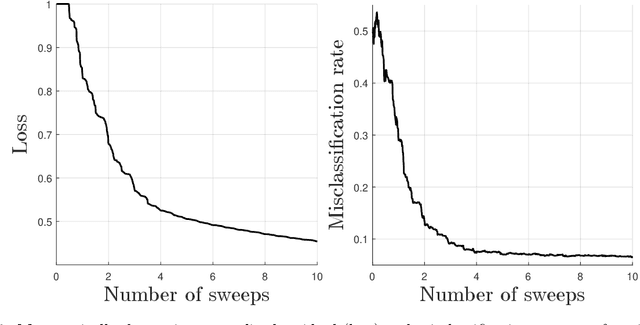
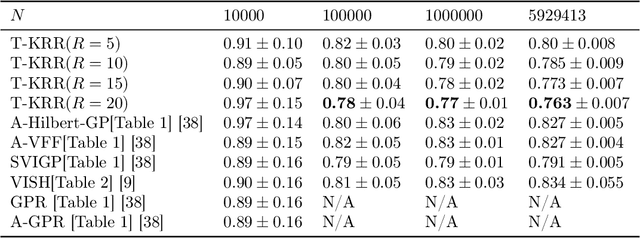
Random Fourier features provide a way to tackle large-scale machine learning problems with kernel methods. Their slow Monte Carlo convergence rate has motivated the research of deterministic Fourier features whose approximation error decreases exponentially with the number of frequencies. However, due to their tensor product structure these methods suffer heavily from the curse of dimensionality, limiting their applicability to two or three-dimensional scenarios. In our approach we overcome said curse of dimensionality by exploiting the tensor product structure of deterministic Fourier features, which enables us to represent the model parameters as a low-rank tensor decomposition. We derive a monotonically converging block coordinate descent algorithm with linear complexity in both the sample size and the dimensionality of the inputs for a regularized squared loss function, allowing to learn a parsimonious model in decomposed form using deterministic Fourier features. We demonstrate by means of numerical experiments how our low-rank tensor approach obtains the same performance of the corresponding nonparametric model, consistently outperforming random Fourier features.