Large-Scale Learning with Fourier Features and Tensor Decompositions
Paper and Code
Sep 03, 2021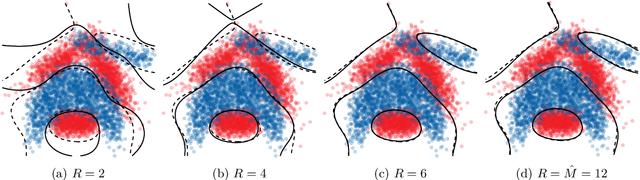

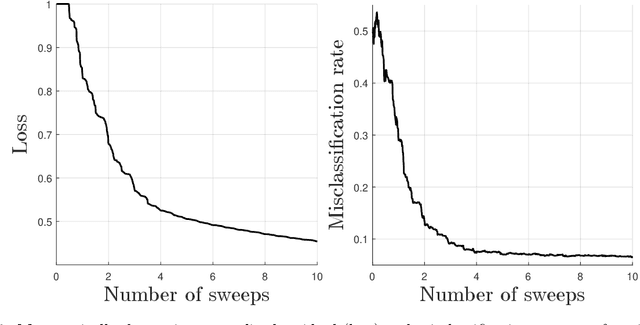
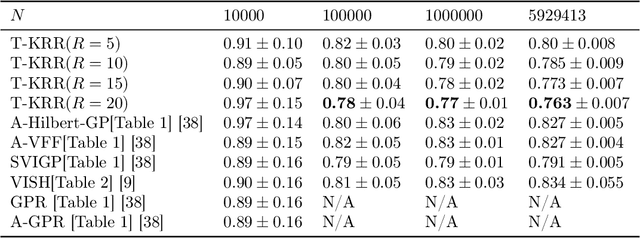
Random Fourier features provide a way to tackle large-scale machine learning problems with kernel methods. Their slow Monte Carlo convergence rate has motivated the research of deterministic Fourier features whose approximation error decreases exponentially with the number of frequencies. However, due to their tensor product structure these methods suffer heavily from the curse of dimensionality, limiting their applicability to two or three-dimensional scenarios. In our approach we overcome said curse of dimensionality by exploiting the tensor product structure of deterministic Fourier features, which enables us to represent the model parameters as a low-rank tensor decomposition. We derive a monotonically converging block coordinate descent algorithm with linear complexity in both the sample size and the dimensionality of the inputs for a regularized squared loss function, allowing to learn a parsimonious model in decomposed form using deterministic Fourier features. We demonstrate by means of numerical experiments how our low-rank tensor approach obtains the same performance of the corresponding nonparametric model, consistently outperforming random Fourier features.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge