A Kernelizable Primal-Dual Formulation of the Multilinear Singular Value Decomposition

The ability to express a learning task in terms of a primal and a dual optimization problem lies at the core of a plethora of machine learning methods. For example, Support Vector Machine (SVM), Least-Squares Support Vector Machine (LS-SVM), Ridge Regression (RR), Lasso Regression (LR), Principal Component Analysis (PCA), and more recently Singular Value Decomposition (SVD) have all been defined either in terms of primal weights or in terms of dual Lagrange multipliers. The primal formulation is computationally advantageous in the case of large sample size while the dual is preferred for high-dimensional data. Crucially, said learning problems can be made nonlinear through the introduction of a feature map in the primal problem, which corresponds to applying the kernel trick in the dual. In this paper we derive a primal-dual formulation of the Multilinear Singular Value Decomposition (MLSVD), which recovers as special cases both PCA and SVD. Besides enabling computational gains through the derived primal formulation, we propose a nonlinear extension of the MLSVD using feature maps, which results in a dual problem where a kernel tensor arises. We discuss potential applications in the context of signal analysis and deep learning.

Tensor network square root Kalman filter for online Gaussian process regression

The state-of-the-art tensor network Kalman filter lifts the curse of dimensionality for high-dimensional recursive estimation problems. However, the required rounding operation can cause filter divergence due to the loss of positive definiteness of covariance matrices. We solve this issue by developing, for the first time, a tensor network square root Kalman filter, and apply it to high-dimensional online Gaussian process regression. In our experiments, we demonstrate that our method is equivalent to the conventional Kalman filter when choosing a full-rank tensor network. Furthermore, we apply our method to a real-life system identification problem where we estimate $4^{14}$ parameters on a standard laptop. The estimated model outperforms the state-of-the-art tensor network Kalman filter in terms of prediction accuracy and uncertainty quantification.

Constructing structured tensor priors for Bayesian inverse problems

Specifying a prior distribution is an essential part of solving Bayesian inverse problems. The prior encodes a belief on the nature of the solution and this regularizes the problem. In this article we completely characterize a Gaussian prior that encodes the belief that the solution is a structured tensor. We first define the notion of (A,b)-constrained tensors and show that they describe a large variety of different structures such as Hankel, circulant, triangular, symmetric, and so on. Then we completely characterize the Gaussian probability distribution of such tensors by specifying its mean vector and covariance matrix. Furthermore, explicit expressions are proved for the covariance matrix of tensors whose entries are invariant under a permutation. These results unlock a whole new class of priors for Bayesian inverse problems. We illustrate how new kernel functions can be designed and efficiently computed and apply our results on two particular Bayesian inverse problems: completing a Hankel matrix from a few noisy measurements and learning an image classifier of handwritten digits. The effectiveness of the proposed priors is demonstrated for both problems. All applications have been implemented as reactive Pluto notebooks in Julia.

Tensor Network-Constrained Kernel Machines as Gaussian Processes

Tensor Networks (TNs) have recently been used to speed up kernel machines by constraining the model weights, yielding exponential computational and storage savings. In this paper we prove that the outputs of Canonical Polyadic Decomposition (CPD) and Tensor Train (TT)-constrained kernel machines recover a Gaussian Process (GP), which we fully characterize, when placing i.i.d. priors over their parameters. We analyze the convergence of both CPD and TT-constrained models, and show how TT yields models exhibiting more GP behavior compared to CPD, for the same number of model parameters. We empirically observe this behavior in two numerical experiments where we respectively analyze the convergence to the GP and the performance at prediction. We thereby establish a connection between TN-constrained kernel machines and GPs.

A divide-and-conquer approach for sparse recovery of high dimensional signals

Compressed sensing (CS) techniques demand significant storage and computational resources, when recovering high-dimensional sparse signals. Block CS (BCS), a special class of CS, addresses both the storage and complexity issues by partitioning the sparse recovery problem into several sub-problems. In this paper, we derive a Welch bound-based guarantee on the reconstruction error with BCS. Our guarantee reveals that the reconstruction quality with BCS monotonically reduces with an increasing number of partitions. To alleviate this performance loss, we propose a sparse recovery technique that exploits correlation across the partitions of the sparse signal. Our method outperforms BCS in the moderate SNR regime, for a modest increase in the storage and computational complexities.

Projecting basis functions with tensor networks for Gaussian process regression

This paper presents a method for approximate Gaussian process (GP) regression with tensor networks (TNs). A parametric approximation of a GP uses a linear combination of basis functions, where the accuracy of the approximation depends on the total number of basis functions $M$. We develop an approach that allows us to use an exponential amount of basis functions without the corresponding exponential computational complexity. The key idea to enable this is using low-rank TNs. We first find a suitable low-dimensional subspace from the data, described by a low-rank TN. In this low-dimensional subspace, we then infer the weights of our model by solving a Bayesian inference problem. Finally, we project the resulting weights back to the original space to make GP predictions. The benefit of our approach comes from the projection to a smaller subspace: It modifies the shape of the basis functions in a way that it sees fit based on the given data, and it allows for efficient computations in the smaller subspace. In an experiment with an 18-dimensional benchmark data set, we show the applicability of our method to an inverse dynamics problem.

Quantized Fourier and Polynomial Features for more Expressive Tensor Network Models

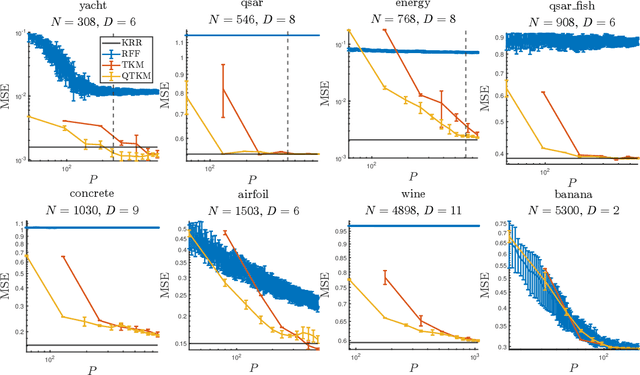
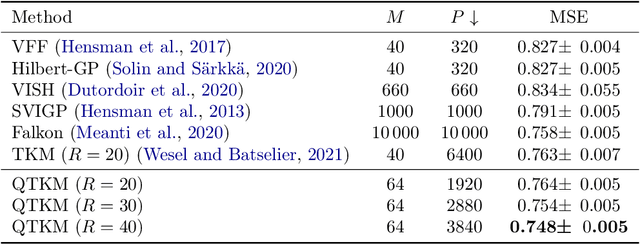
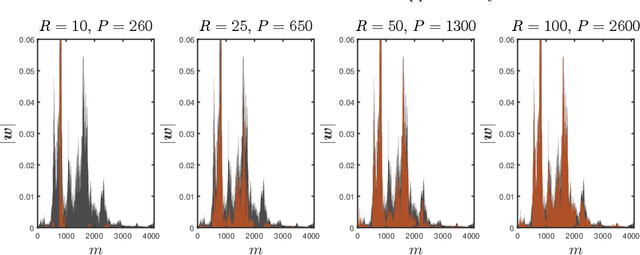
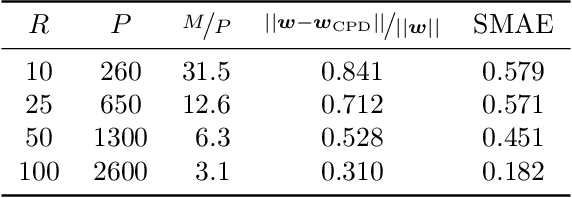
In the context of kernel machines, polynomial and Fourier features are commonly used to provide a nonlinear extension to linear models by mapping the data to a higher-dimensional space. Unless one considers the dual formulation of the learning problem, which renders exact large-scale learning unfeasible, the exponential increase of model parameters in the dimensionality of the data caused by their tensor-product structure prohibits to tackle high-dimensional problems. One of the possible approaches to circumvent this exponential scaling is to exploit the tensor structure present in the features by constraining the model weights to be an underparametrized tensor network. In this paper we quantize, i.e. further tensorize, polynomial and Fourier features. Based on this feature quantization we propose to quantize the associated model weights, yielding quantized models. We show that, for the same number of model parameters, the resulting quantized models have a higher bound on the VC-dimension as opposed to their non-quantized counterparts, at no additional computational cost while learning from identical features. We verify experimentally how this additional tensorization regularizes the learning problem by prioritizing the most salient features in the data and how it provides models with increased generalization capabilities. We finally benchmark our approach on large regression task, achieving state-of-the-art results on a laptop computer.

How Informative is the Approximation Error from Tensor Decomposition for Neural Network Compression?

Tensor decompositions have been successfully applied to compress neural networks. The compression algorithms using tensor decompositions commonly minimize the approximation error on the weights. Recent work assumes the approximation error on the weights is a proxy for the performance of the model to compress multiple layers and fine-tune the compressed model. Surprisingly, little research has systematically evaluated which approximation errors can be used to make choices regarding the layer, tensor decomposition method, and level of compression. To close this gap, we perform an experimental study to test if this assumption holds across different layers and types of decompositions, and what the effect of fine-tuning is. We include the approximation error on the features resulting from a compressed layer in our analysis to test if this provides a better proxy, as it explicitly takes the data into account. We find the approximation error on the weights has a positive correlation with the performance error, before as well as after fine-tuning. Basing the approximation error on the features does not improve the correlation significantly. While scaling the approximation error commonly is used to account for the different sizes of layers, the average correlation across layers is smaller than across all choices (i.e. layers, decompositions, and level of compression) before fine-tuning. When calculating the correlation across the different decompositions, the average rank correlation is larger than across all choices. This means multiple decompositions can be considered for compression and the approximation error can be used to choose between them.

Towards Green AI with tensor networks -- Sustainability and innovation enabled by efficient algorithms

The current standard to compare the performance of AI algorithms is mainly based on one criterion: the model's accuracy. In this context, algorithms with a higher accuracy (or similar measures) are considered as better. To achieve new state-of-the-art results, algorithmic development is accompanied by an exponentially increasing amount of compute. While this has enabled AI research to achieve remarkable results, AI progress comes at a cost: it is unsustainable. In this paper, we present a promising tool for sustainable and thus Green AI: tensor networks (TNs). Being an established tool from multilinear algebra, TNs have the capability to improve efficiency without compromising accuracy. Since they can reduce compute significantly, we would like to highlight their potential for Green AI. We elaborate in both a kernel machine and deep learning setting how efficiency gains can be achieved with TNs. Furthermore, we argue that better algorithms should be evaluated in terms of both accuracy and efficiency. To that end, we discuss different efficiency criteria and analyze efficiency in an exemplifying experimental setting for kernel ridge regression. With this paper, we want to raise awareness about Green AI and showcase its positive impact on sustainability and AI research. Our key contribution is to demonstrate that TNs enable efficient algorithms and therefore contribute towards Green AI. In this sense, TNs pave the way for better algorithms in AI.

Tensor Network Kalman Filtering for Large-Scale LS-SVMs

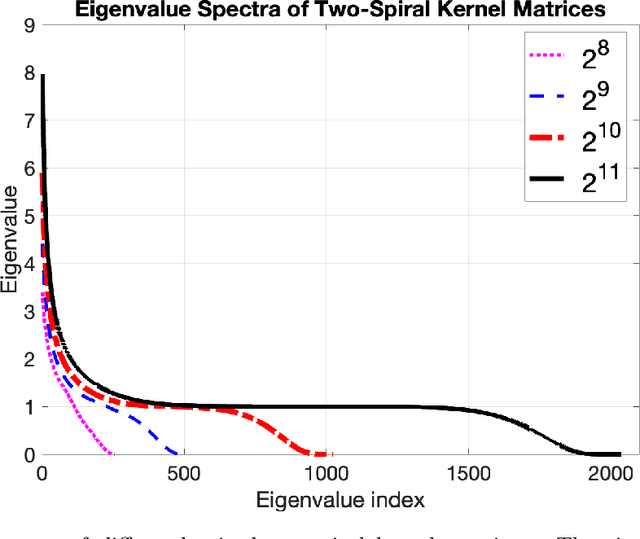
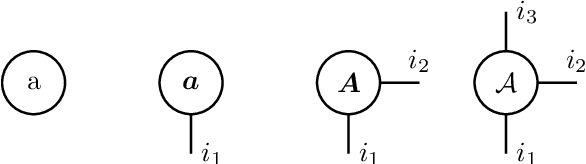
Least squares support vector machines are a commonly used supervised learning method for nonlinear regression and classification. They can be implemented in either their primal or dual form. The latter requires solving a linear system, which can be advantageous as an explicit mapping of the data to a possibly infinite-dimensional feature space is avoided. However, for large-scale applications, current low-rank approximation methods can perform inadequately. For example, current methods are probabilistic due to their sampling procedures, and/or suffer from a poor trade-off between the ranks and approximation power. In this paper, a recursive Bayesian filtering framework based on tensor networks and the Kalman filter is presented to alleviate the demanding memory and computational complexities associated with solving large-scale dual problems. The proposed method is iterative, does not require explicit storage of the kernel matrix, and allows the formulation of early stopping conditions. Additionally, the framework yields confidence estimates of obtained models, unlike alternative methods. The performance is tested on two regression and three classification experiments, and compared to the Nystr\"om and fixed size LS-SVM methods. Results show that our method can achieve high performance and is particularly useful when alternative methods are computationally infeasible due to a slowly decaying kernel matrix spectrum.