Tensor Network Kalman Filtering for Large-Scale LS-SVMs
Paper and Code
Oct 26, 2021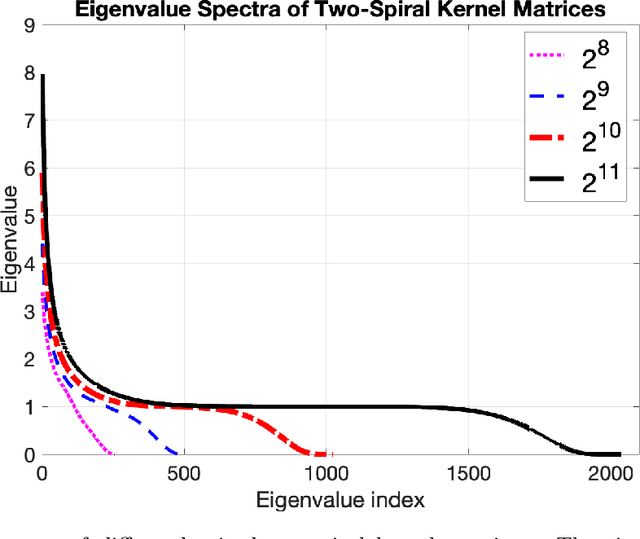
Least squares support vector machines are a commonly used supervised learning method for nonlinear regression and classification. They can be implemented in either their primal or dual form. The latter requires solving a linear system, which can be advantageous as an explicit mapping of the data to a possibly infinite-dimensional feature space is avoided. However, for large-scale applications, current low-rank approximation methods can perform inadequately. For example, current methods are probabilistic due to their sampling procedures, and/or suffer from a poor trade-off between the ranks and approximation power. In this paper, a recursive Bayesian filtering framework based on tensor networks and the Kalman filter is presented to alleviate the demanding memory and computational complexities associated with solving large-scale dual problems. The proposed method is iterative, does not require explicit storage of the kernel matrix, and allows the formulation of early stopping conditions. Additionally, the framework yields confidence estimates of obtained models, unlike alternative methods. The performance is tested on two regression and three classification experiments, and compared to the Nystr\"om and fixed size LS-SVM methods. Results show that our method can achieve high performance and is particularly useful when alternative methods are computationally infeasible due to a slowly decaying kernel matrix spectrum.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge