Adaptive Basis Function Selection for Computationally Efficient Predictions

Basis Function (BF) expansions are a cornerstone of any engineer's toolbox for computational function approximation which shares connections with both neural networks and Gaussian processes. Even though BF expansions are an intuitive and straightforward model to use, they suffer from quadratic computational complexity in the number of BFs if the predictive variance is to be computed. We develop a method to automatically select the most important BFs for prediction in a sub-domain of the model domain. This significantly reduces the computational complexity of computing predictions while maintaining predictive accuracy. The proposed method is demonstrated using two numerical examples, where reductions up to 50-75% are possible without significantly reducing the predictive accuracy.

Exploiting Hankel-Toeplitz Structures for Fast Computation of Kernel Precision Matrices

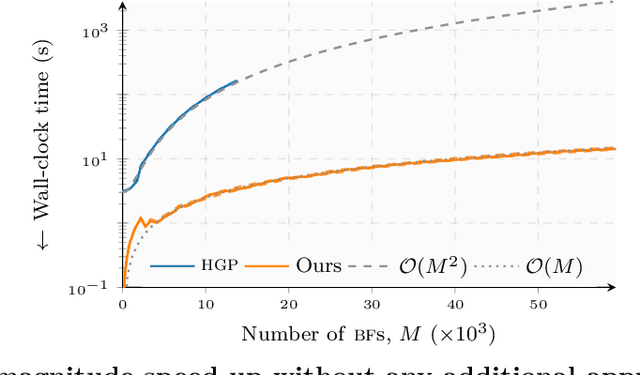
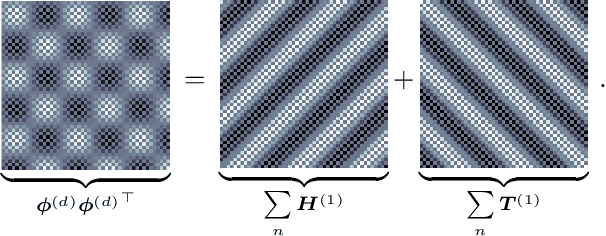
The Hilbert-space Gaussian Process (HGP) approach offers a hyperparameter-independent basis function approximation for speeding up Gaussian Process (GP) inference by projecting the GP onto M basis functions. These properties result in a favorable data-independent $\mathcal{O}(M^3)$ computational complexity during hyperparameter optimization but require a dominating one-time precomputation of the precision matrix costing $\mathcal{O}(NM^2)$ operations. In this paper, we lower this dominating computational complexity to $\mathcal{O}(NM)$ with no additional approximations. We can do this because we realize that the precision matrix can be split into a sum of Hankel-Toeplitz matrices, each having $\mathcal{O}(M)$ unique entries. Based on this realization we propose computing only these unique entries at $\mathcal{O}(NM)$ costs. Further, we develop two theorems that prescribe sufficient conditions for the complexity reduction to hold generally for a wide range of other approximate GP models, such as the Variational Fourier Feature (VFF) approach. The two theorems do this with no assumptions on the data and no additional approximations of the GP models themselves. Thus, our contribution provides a pure speed-up of several existing, widely used, GP approximations, without further approximations.

Distributed multi-agent magnetic field norm SLAM with Gaussian processes

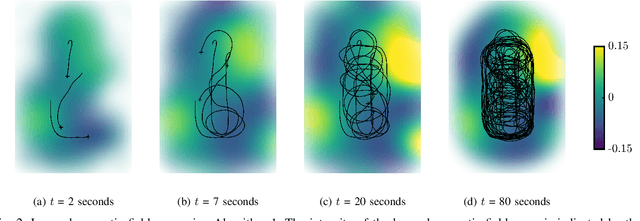
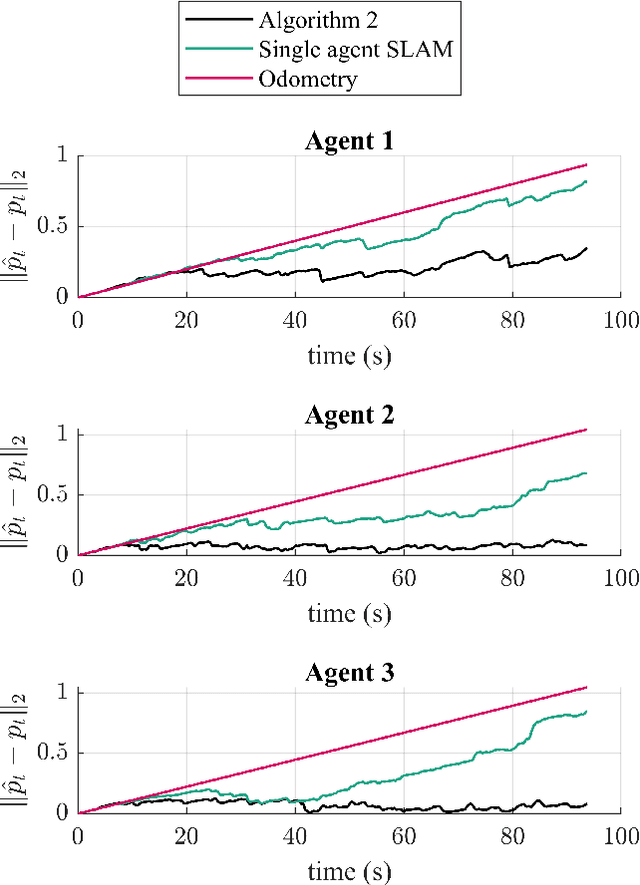
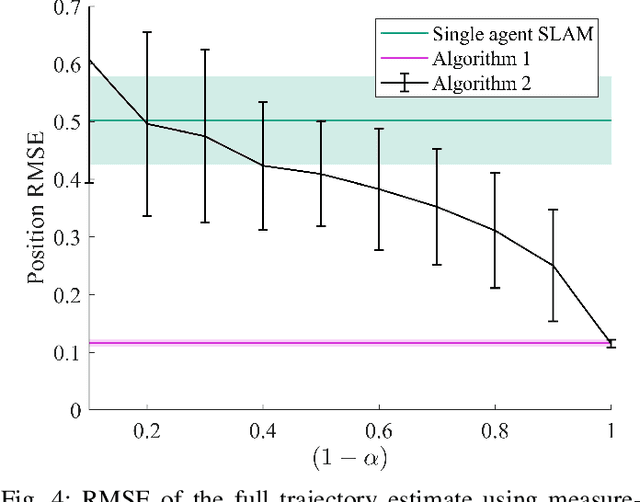
Accurately estimating the positions of multi-agent systems in indoor environments is challenging due to the lack of Global Navigation Satelite System (GNSS) signals. Noisy measurements of position and orientation can cause the integrated position estimate to drift without bound. Previous research has proposed using magnetic field simultaneous localization and mapping (SLAM) to compensate for position drift in a single agent. Here, we propose two novel algorithms that allow multiple agents to apply magnetic field SLAM using their own and other agents measurements. Our first algorithm is a centralized approach that uses all measurements collected by all agents in a single extended Kalman filter. This algorithm simultaneously estimates the agents position and orientation and the magnetic field norm in a central unit that can communicate with all agents at all times. In cases where a central unit is not available, and there are communication drop-outs between agents, our second algorithm is a distributed approach that can be employed. We tested both algorithms by estimating the position of magnetometers carried by three people in an optical motion capture lab with simulated odometry and simulated communication dropouts between agents. We show that both algorithms are able to compensate for drift in a case where single-agent SLAM is not. We also discuss the conditions for the estimate from our distributed algorithm to converge to the estimate from the centralized algorithm, both theoretically and experimentally. Our experiments show that, for a communication drop-out rate of 80 percent, our proposed distributed algorithm, on average, provides a more accurate position estimate than single-agent SLAM. Finally, we demonstrate the drift-compensating abilities of our centralized algorithm on a real-life pedestrian localization problem with multiple agents moving inside a building.

Indoor SLAM Using a Foot-mounted IMU and the local Magnetic Field

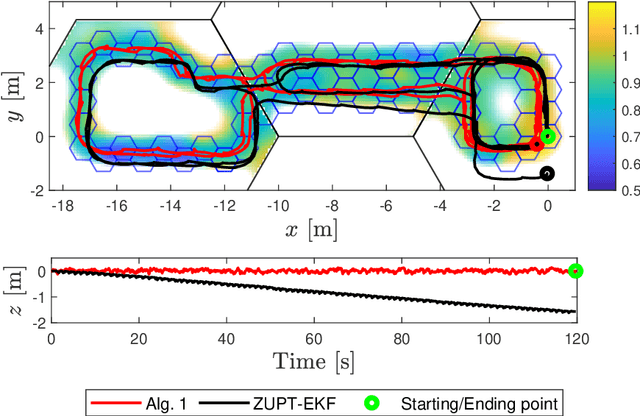
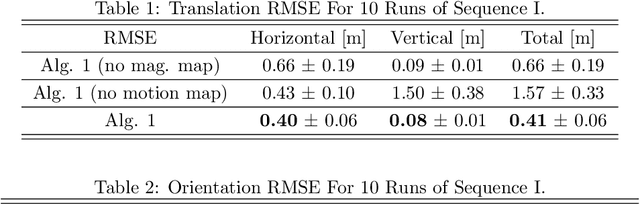
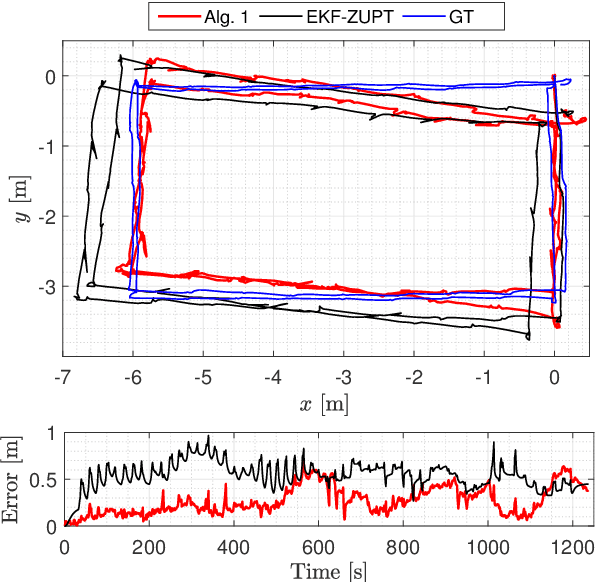
In this paper, a simultaneous localization and mapping (SLAM) algorithm for tracking the motion of a pedestrian with a foot-mounted inertial measurement unit (IMU) is proposed. The algorithm uses two maps, namely, a motion map and a magnetic field map. The motion map captures typical motion patterns of pedestrians in buildings that are constrained by e.g. corridors and doors. The magnetic map models local magnetic field anomalies in the environment using a Gaussian process (GP) model and uses them as position information. These maps are used in a Rao-Blackwellized particle filter (RBPF) to correct the pedestrian position and orientation estimates from the pedestrian dead-reckoning (PDR). The PDR is computed using an extended Kalman filter with zero-velocity updates (ZUPT-EKF). The algorithm is validated using real experimental sequences and the results show the efficacy of the algorithm in localizing pedestrians in indoor environments.