Robust Prediction when Features are Missing

Predictors are learned using past training data containing features which may be unavailable at the time of prediction. We develop an prediction approach that is robust against unobserved outliers of the missing features, based on the optimality properties of a predictor which has access to these features. The robustness properties of the approach are demonstrated in real and synthetic data.

Robust Semi-Supervised Learning when Labels are Missing at Random

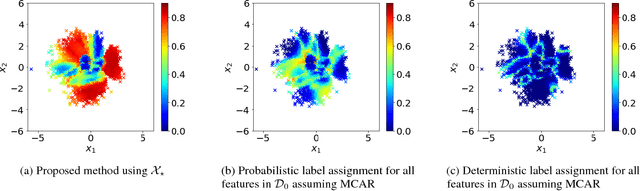
Semi-supervised learning methods are motivated by the relative paucity of labeled data and aim to utilize large sources of unlabeled data to improve predictive tasks. It has been noted, however, such improvements are not guaranteed in general in some cases the unlabeled data impairs the performance. A fundamental source of error comes from restrictive assumptions about the unlabeled features. In this paper, we develop a semi-supervised learning approach that relaxes such assumptions and is robust with respect to labels missing at random. The approach ensures that uncertainty about the classes is propagated to the unlabeled features in a robust manner. It is applicable using any generative model with associated learning algorithm. We illustrate the approach using both standard synthetic data examples and the MNIST data with unlabeled adversarial examples.

Composite Gaussian Processes: Scalable Computation and Performance Analysis

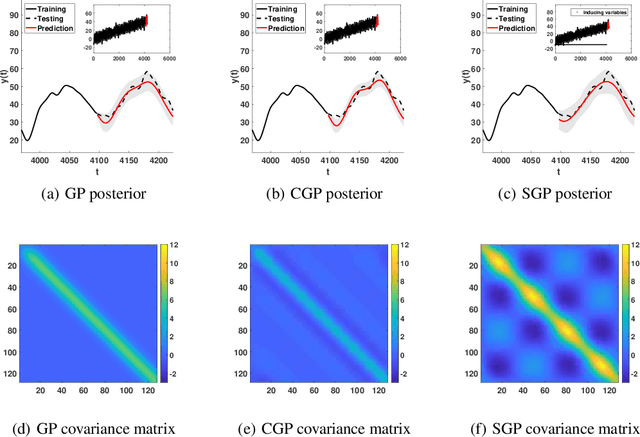
Gaussian process (GP) models provide a powerful tool for prediction but are computationally prohibitive using large data sets. In such scenarios, one has to resort to approximate methods. We derive an approximation based on a composite likelihood approach using a general belief updating framework, which leads to a recursive computation of the predictor as well as of learning the hyper-parameters. We then provide an analysis of the derived composite GP model in predictive and information-theoretic terms. Finally, we evaluate the approximation with both synthetic data and a real-world application.