Marginalized particle Gibbs for multiple state-space models coupled through shared parameters

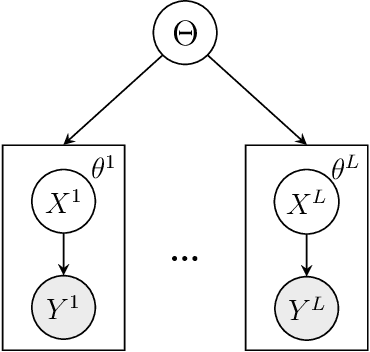
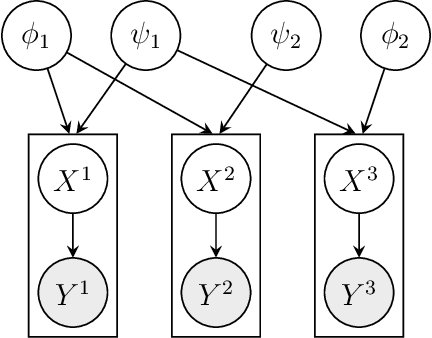
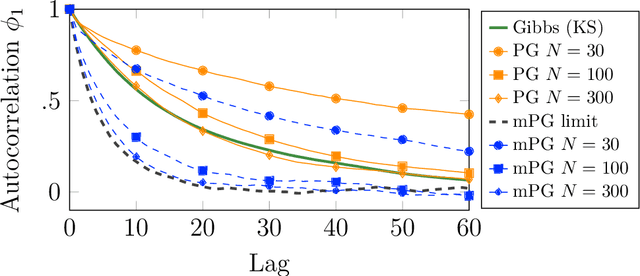
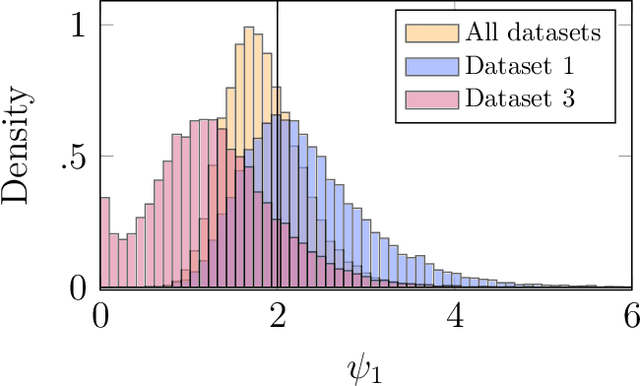
We consider Bayesian inference from multiple time series described by a common state-space model (SSM) structure, but where different subsets of parameters are shared between different submodels. An important example is disease-dynamics, where parameters can be either disease or location specific. Parameter inference in these models can be improved by systematically aggregating information from the different time series, most notably for short series. Particle Gibbs (PG) samplers are an efficient class of algorithms for inference in SSMs, in particular when conjugacy can be exploited to marginalize out model parameters from the state update. We present two different PG samplers that marginalize static model parameters on-the-fly: one that updates one model at a time conditioned on the datasets for the other models, and one that concurrently updates all models by stacking them into a high-dimensional SSM. The distinctive features of each sampler make them suitable for different modelling contexts. We provide insights on when each sampler should be used and show that they can be combined to form an efficient PG sampler for a model with strong dependencies between states and parameters. The performance is illustrated on two linear-Gaussian examples and on a real-world example on the spread of mosquito-borne diseases.

Parameter elimination in particle Gibbs sampling

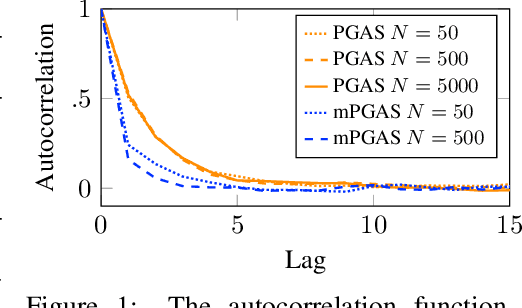
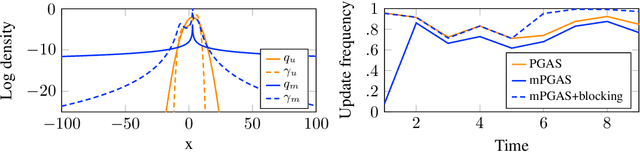
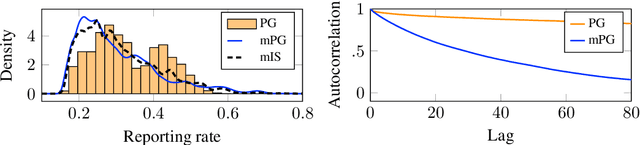
Bayesian inference in state-space models is challenging due to high-dimensional state trajectories. A viable approach is particle Markov chain Monte Carlo, combining MCMC and sequential Monte Carlo to form "exact approximations" to otherwise intractable MCMC methods. The performance of the approximation is limited to that of the exact method. We focus on particle Gibbs and particle Gibbs with ancestor sampling, improving their performance beyond that of the underlying Gibbs sampler (which they approximate) by marginalizing out one or more parameters. This is possible when the parameter prior is conjugate to the complete data likelihood. Marginalization yields a non-Markovian model for inference, but we show that, in contrast to the general case, this method still scales linearly in time. While marginalization can be cumbersome to implement, recent advances in probabilistic programming have enabled its automation. We demonstrate how the marginalized methods are viable as efficient inference backends in probabilistic programming, and demonstrate with examples in ecology and epidemiology.