Marginalized particle Gibbs for multiple state-space models coupled through shared parameters
Paper and Code
Oct 13, 2022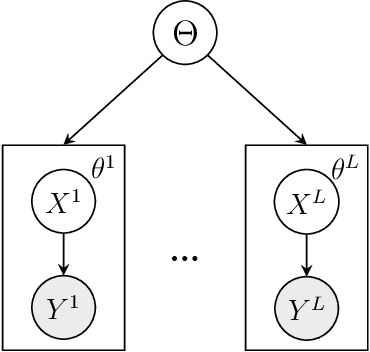
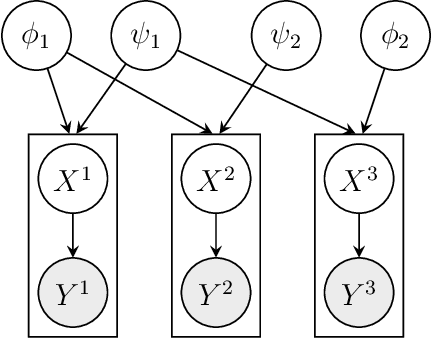
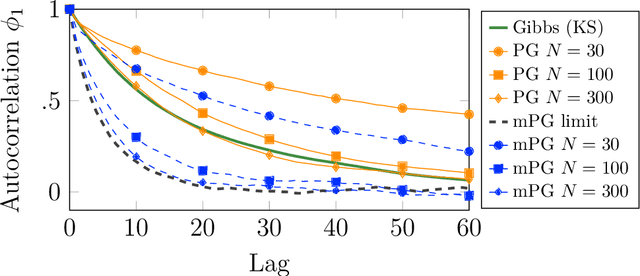
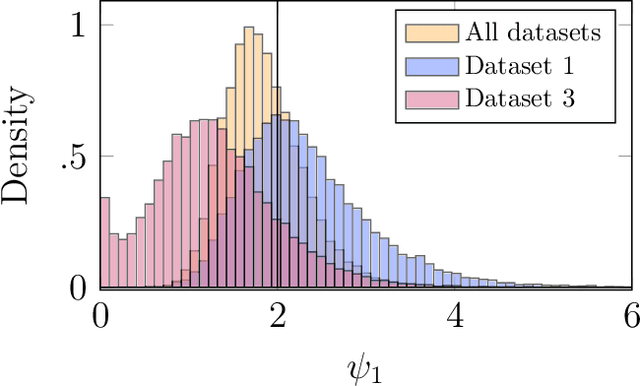
We consider Bayesian inference from multiple time series described by a common state-space model (SSM) structure, but where different subsets of parameters are shared between different submodels. An important example is disease-dynamics, where parameters can be either disease or location specific. Parameter inference in these models can be improved by systematically aggregating information from the different time series, most notably for short series. Particle Gibbs (PG) samplers are an efficient class of algorithms for inference in SSMs, in particular when conjugacy can be exploited to marginalize out model parameters from the state update. We present two different PG samplers that marginalize static model parameters on-the-fly: one that updates one model at a time conditioned on the datasets for the other models, and one that concurrently updates all models by stacking them into a high-dimensional SSM. The distinctive features of each sampler make them suitable for different modelling contexts. We provide insights on when each sampler should be used and show that they can be combined to form an efficient PG sampler for a model with strong dependencies between states and parameters. The performance is illustrated on two linear-Gaussian examples and on a real-world example on the spread of mosquito-borne diseases.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge