The Klarna Product Page Dataset: A Realistic Benchmark for Web Representation Learning

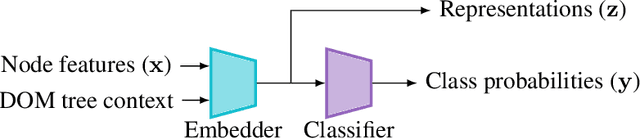
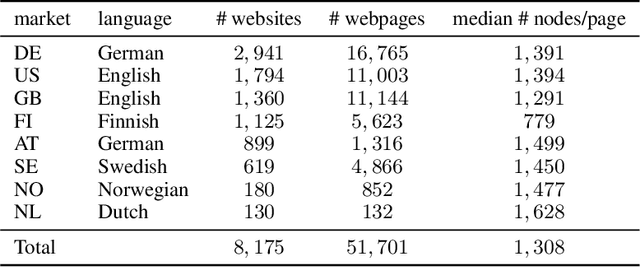
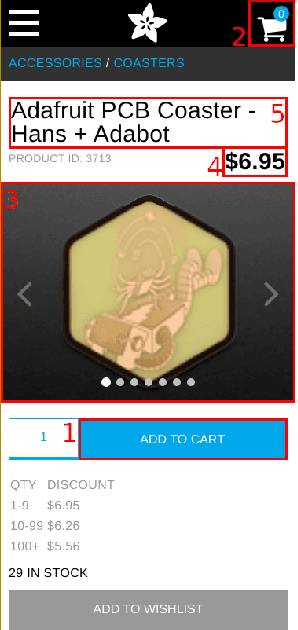
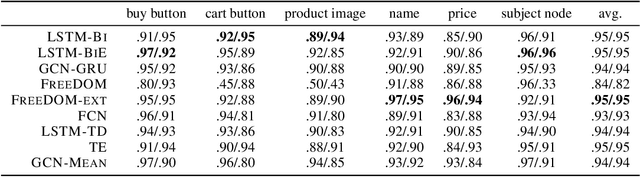
This paper tackles the under-explored problem of DOM tree element representation learning. We advance the field of machine learning-based web automation and hope to spur further research regarding this crucial area with two contributions. First, we adapt several popular Graph-based Neural Network models and apply them to embed elements in website DOM trees. Second, we present a large-scale and realistic dataset of webpages. By providing this open-access resource, we lower the entry barrier to this area of research. The dataset contains $51,701$ manually labeled product pages from $8,175$ real e-commerce websites. The pages can be rendered entirely in a web browser and are suitable for computer vision applications. This makes it substantially richer and more diverse than other datasets proposed for element representation learning, classification and prediction on the web. Finally, using our proposed dataset, we show that the embeddings produced by a Graph Convolutional Neural Network outperform representations produced by other state-of-the-art methods in a web element prediction task.

Online Learning of Optimally Diverse Rankings

Search engines answer users' queries by listing relevant items (e.g. documents, songs, products, web pages, ...). These engines rely on algorithms that learn to rank items so as to present an ordered list maximizing the probability that it contains relevant item. The main challenge in the design of learning-to-rank algorithms stems from the fact that queries often have different meanings for different users. In absence of any contextual information about the query, one often has to adhere to the {\it diversity} principle, i.e., to return a list covering the various possible topics or meanings of the query. To formalize this learning-to-rank problem, we propose a natural model where (i) items are categorized into topics, (ii) users find items relevant only if they match the topic of their query, and (iii) the engine is not aware of the topic of an arriving query, nor of the frequency at which queries related to various topics arrive, nor of the topic-dependent click-through-rates of the items. For this problem, we devise LDR (Learning Diverse Rankings), an algorithm that efficiently learns the optimal list based on users' feedback only. We show that after $T$ queries, the regret of LDR scales as $O((N-L)\log(T))$ where $N$ is the number of all items. We further establish that this scaling cannot be improved, i.e., LDR is order optimal. Finally, using numerical experiments on both artificial and real-world data, we illustrate the superiority of LDR compared to existing learning-to-rank algorithms.

Minimal Exploration in Structured Stochastic Bandits

This paper introduces and addresses a wide class of stochastic bandit problems where the function mapping the arm to the corresponding reward exhibits some known structural properties. Most existing structures (e.g. linear, Lipschitz, unimodal, combinatorial, dueling, ...) are covered by our framework. We derive an asymptotic instance-specific regret lower bound for these problems, and develop OSSB, an algorithm whose regret matches this fundamental limit. OSSB is not based on the classical principle of "optimism in the face of uncertainty" or on Thompson sampling, and rather aims at matching the minimal exploration rates of sub-optimal arms as characterized in the derivation of the regret lower bound. We illustrate the efficiency of OSSB using numerical experiments in the case of the linear bandit problem and show that OSSB outperforms existing algorithms, including Thompson sampling.

Lipschitz Bandits: Regret Lower Bounds and Optimal Algorithms

We consider stochastic multi-armed bandit problems where the expected reward is a Lipschitz function of the arm, and where the set of arms is either discrete or continuous. For discrete Lipschitz bandits, we derive asymptotic problem specific lower bounds for the regret satisfied by any algorithm, and propose OSLB and CKL-UCB, two algorithms that efficiently exploit the Lipschitz structure of the problem. In fact, we prove that OSLB is asymptotically optimal, as its asymptotic regret matches the lower bound. The regret analysis of our algorithms relies on a new concentration inequality for weighted sums of KL divergences between the empirical distributions of rewards and their true distributions. For continuous Lipschitz bandits, we propose to first discretize the action space, and then apply OSLB or CKL-UCB, algorithms that provably exploit the structure efficiently. This approach is shown, through numerical experiments, to significantly outperform existing algorithms that directly deal with the continuous set of arms. Finally the results and algorithms are extended to contextual bandits with similarities.