A new kernel-based approach for overparameterized Hammerstein system identification
Paper and Code
May 18, 2016
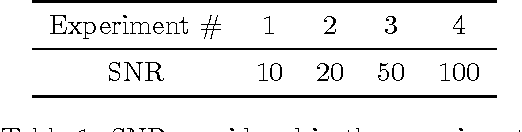
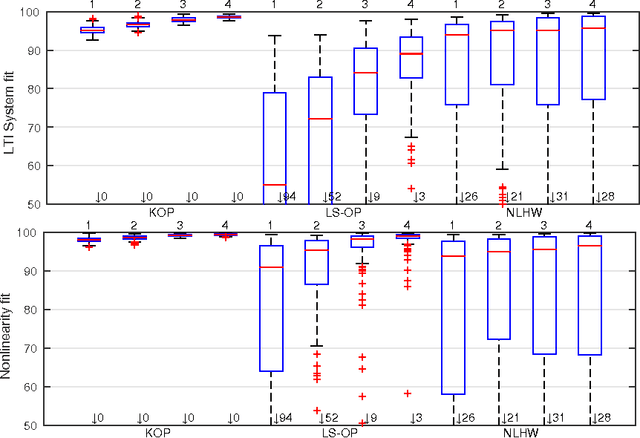
In this paper we propose a new identification scheme for Hammerstein systems, which are dynamic systems consisting of a static nonlinearity and a linear time-invariant dynamic system in cascade. We assume that the nonlinear function can be described as a linear combination of $p$ basis functions. We reconstruct the $p$ coefficients of the nonlinearity together with the first $n$ samples of the impulse response of the linear system by estimating an $np$-dimensional overparameterized vector, which contains all the combinations of the unknown variables. To avoid high variance in these estimates, we adopt a regularized kernel-based approach and, in particular, we introduce a new kernel tailored for Hammerstein system identification. We show that the resulting scheme provides an estimate of the overparameterized vector that can be uniquely decomposed as the combination of an impulse response and $p$ coefficients of the static nonlinearity. We also show, through several numerical experiments, that the proposed method compares very favorably with two standard methods for Hammerstein system identification.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge