Bayesian kernel-based system identification with quantized output data
Paper and Code
Apr 26, 2015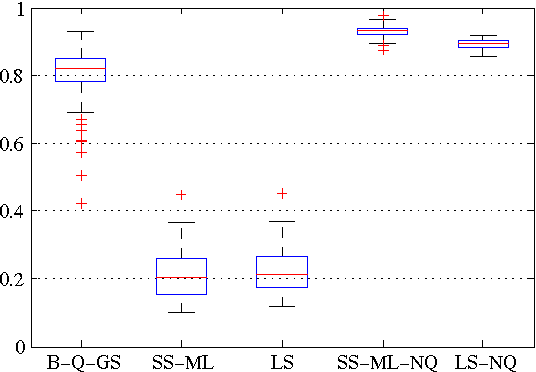
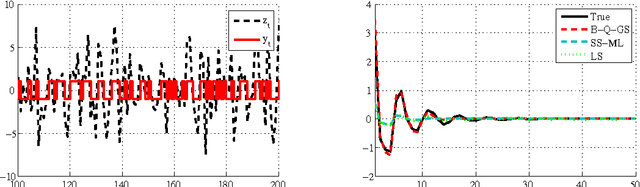
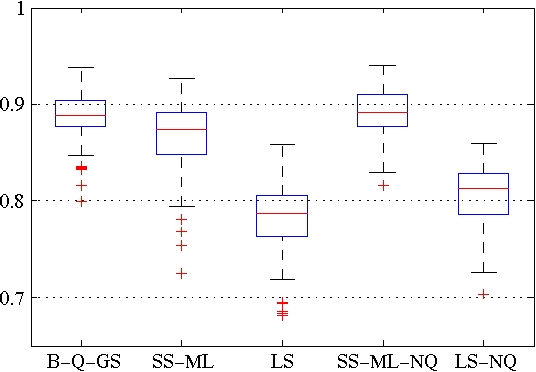
In this paper we introduce a novel method for linear system identification with quantized output data. We model the impulse response as a zero-mean Gaussian process whose covariance (kernel) is given by the recently proposed stable spline kernel, which encodes information on regularity and exponential stability. This serves as a starting point to cast our system identification problem into a Bayesian framework. We employ Markov Chain Monte Carlo (MCMC) methods to provide an estimate of the system. In particular, we show how to design a Gibbs sampler which quickly converges to the target distribution. Numerical simulations show a substantial improvement in the accuracy of the estimates over state-of-the-art kernel-based methods when employed in identification of systems with quantized data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge